656_Lytkina_D.V._Algebraicheskie_struktury_

УДК 512

Утверждено редакционно-издательским советом СибГУТИ

Рецензенты: д.ф.-м.н. Мазуров В.Д.

д.ф.-м.н. Судоплатов С.В.

Лыткина Д. В., Храмова Т. В. Алгебраические структуры : Учебное пособие / Сибирский государственный университет телекоммуникаций и информатики. – Новосибирск, 2016. – 108 с.

Пособие предназначено для использования в учебном процессе преподавателями и студентами высших учебных заведений при изучении математики в соответствии с ФГОС по направлениям подготовки бакалавров 02.03.02 «Фундаментальная информатика и информационные технологии» и 01.03.02 «Прикладная математика и информатика».

В авторской редакции

© Лыткина Д. В., Храмова Т. В., 2016

© Сибирский государственный университет телекоммуникаций и информатики, 2016

2

Оглавление

3

1. Элементы теории множеств

Множество – это совокупность различимых элементов. Для обозначения того факта, что элемент x принадлежит (не принадлежит) множеству M , будем использовать обозначение x M (x M ). Множество, не содержащее ни одного элемента, называется пустым и обозначается как .

В дальнейшем для компактности записей будем использовать кванторы, а именно:

«» – квантор всеобщности, читается как «для любого», «каждый»;

«» – квантор существования, читается как «существует», «найдется».

Кроме того, будем использовать общепринятые обозначения:

« : » или « | » – «такой, что»;

«» – «следовательно», «значит»;

«» – «равносильно», «тогда и только тогда».

Например, запись

x y : y x

читается как «для любого действительного числа x найдется действительное число y, такое, что y меньше x».

Запись M x|P(x) читается как «множество M состоит из элементов x, для которых выполняется условие P(x)».

Если все элементы множества A являются элементами множества B, то

A называется подмножеством множества B (A включено в B):

Знак включения может быть строгим:

Множества равны, если они включены друг в друга:

A B и B A A B.

Декартово произведение множеств A1 A2 ... An состоит из

упорядоченных n-ок, в которых i-й элемент принадлежит множеству Ai, i 1, n, n (запись i 1,n означает, что i 1,2,...,n):

A1 A2 ... An a1,a2,...,an |ai Ai,i 1,n .

Частный случай декартова произведения – декартова степень множества:

An a1,a2,...,an |ai A,i 1,n

4

Любое подмножество R декартова произведения A B называется отношением на множествах A и B. Если пара (a,b) принадлежит отношению, то будем говорить, что aиb соответствуют друг другу.

множества В соответствует единственный элемент из А, то функция называется

Бинарные алгебраические операции могут обладать (или не обладать) следующими свойствами:

ассоциативность операции :

x,y,z M x (y z) (x y) z;

коммутативность операции :

x,y M x y y x;

дистрибутивность операции относительно операции

слева: x,y,z M x (y z) x y x z ,

справа: x,y,z M (y z) x y x z x .

Пример. Рассмотрим алгебраические операции сложения, вычитания, умножения и деления на множестве действительных чисел .

Сложение и умножение ассоциативны:

x (y z) (x y) z , x (y z) (x y) z ,

авычитание и деление свойством ассоциативности не обладают:

x(y z) x y z (x y) z (x y) z,

x:(y:z) x zy (x z): y,

5

(x:y):z xy 1z x:(y z).

Кроме того, легко проверить, что сложение и умножение коммутативны, а вычитание и деление – нет.

Дистрибутивность имеет место для следующих алгебраических операций:

умножение относительно сложения и слева, и справа:

x (y z) (x y) (x z), (x y) z (x z) (y z);

умножение относительно вычитания и слева, и справа:

x (y z) (x y) (x z),

(x y) z (x z) (y z);

деление относительно сложения справа:

(x y):z x z y xz yz (x:z) (y:z);

деление относительно вычитания справа:

(x y):z x z y xz yz (x:z) (y:z).

Деление относительно сложения (или вычитания) не обладает свойством дистрибутивности слева:

x:(y z) yx z xy xz ,

(например, 4:(1 4) 144 0,8, а (4:1) (4:4) 4 1 5).

Сложение и вычитание, как и умножение и деление, не обладают свойством дистрибутивности относительно друг друга ни справа, ни слева. █

Определим основные операции над множествами:

дополнение A множества A – это все элементы, не принадлежащие A:

A x|x A ;

объединение A B множеств состоит из элементов, принадлежащих A или B:

A B x| x Aили x B ;

пересечение A B множеств состоит из элементов, принадлежащих и A, и B:

A B x|x Aи x B ;

6

разность A\B множеств состоит из элементов, принадлежащих A, но не принадлежащих B:

A\B x|x Aи x B .

Объединение и пересечение можно рассматривать и в n-мерном случае для любого конечного числа множеств:

n

Ai A1 A2 ... An x| i:1 i n x Ai ,

i1

7

2. Алгебраические системы

Алгебраическая система – это множество с определенными на нем алгебраическими операциями:

Замечание. Множество М алгебраической системы 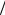M, 1, 2,..., m,

называется основным множеством или носителем. Далее под элементом какой-либо системы будем подразумевать элемент основного множества этой системы. Основное множество может быть как конечным, так и бесконечным. В зависимости от этого и алгебраическую систему называют конечной или бесконечной.

Рассмотрим основные типы алгебраических систем.

Полугруппа – это алгебраическая система M, с одной ассоциативной

алгебраической операцией.

Моноид – это полугруппа M, , содержащая единичный

(нейтральный) относительно алгебраической операции элемент e:

e M : x M e x x e x.

Группа – это моноид M, , в котором для каждого элемента найдется

обратный элемент относительно алгебраической операции:

x M x 1 M :x x 1 x 1 x e.

Замечание. Группа с алгебраической операцией сложения M,

называется аддитивной группой, а ее нейтральный элемент – нулем. Обратный элемент в аддитивной группе принято называть противоположным. Группа с алгебраической операцией умножения M, называется мультипликативной

группой.

Подгруппа группы M, – это группа M', , где M' M .

Абелева группа – это группа с коммутативной операцией.

Кольцо – это алгебраическая система M, , с двумя алгебраическими

операциями (называемыми соответственно сложением и умножением, хотя они могут не совпадать с привычными операциями), такая, что M, – абелева

группа и операция умножения дистрибутивна относительно операции сложения.

Ассоциативное кольцо – это кольцо, в котором операция умножения ассоциативна.

Коммутативное кольцо – это кольцо, в котором операция умножения коммутативна.

8

Кольцо с единицей – это кольцо с нейтральным элементом относительно операции умножения (нейтральный элемент по умножению будем обозначать символом 1).

Поле – это коммутативное и ассоциативное кольцо с единицей, в котором каждый ненулевой элемент обратим (имеет обратный по умножению).

Сформулируем полный список аксиом поля M, , :

3)0 M : x M x 0 0 x x (существование нуля);

4)x M ( x) M :x ( x) ( x) x 0 (существование противоположного);

7)1 M : x M x 1 1 x x (существование единицы);

8)x M \{0} x 1 M :x x 1 x 1 x 1 (существование обратного);

(дистрибутивность умножения относительно сложения слева/справа).

Пример. Доказать, что множество чисел M a b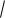3 a,b является

полем относительно операций обычного сложения и умножения.

Решение. Коммутативность, ассоциативность и дистрибутивность операций, очевидно, следует из того, что элементы множества М – действительные числа. Необходимо убедиться, что результат действия операций, нуль, единица, противоположный элемент и обратный элемент являются числами из основного множества М.

Результат сложения является элементом М:

a b3 M

Результат умножения является элементом М:

9

Укаждого элемента М, кроме нуля, есть обратный в М:

a b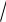3 M, (a,b) (0,0)

Упражнения и задачи

2.1.Доказать, что единичный элемент в группе только один.

2.2.Доказать, что обратный элемент единствен для любого элемента группы.

2.3.Доказать, что в кольце при умножении на нуль всегда получается нуль.

Делителями нуля называются ненулевые элементы системы, произведение которых равно нулю.

2.4.Доказать, что если a 0 и а не является делителем нуля в кольце, то из равенства a b a c следует, что b c.

2.5.Доказать, что в поле нет делителей нуля.

10