
656_Lytkina_D.V._Algebraicheskie_struktury_
.pdf
Еще одним примером кольца, с которым мы сталкивались в курсе алгебры, является кольцо квадратных матриц. Рассмотрим множество Mn( )
всех матриц размера n n с вещественными элементам. Это множество образует кольцо 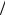 Mn( ), ,
Mn( ), ,  (упр. 4.5).
(упр. 4.5).
Определим элементарную матрицу Eij следующим образом: |
|||
|
|
|
|
|
1, |
m l; |
|
Eij |
|
m i, |
l j; |
, |
|||
ml |
|
|
|
|
иначе. |
|
|
|
0, |
|
|
Легко проверить (упр. 4.6), что, умножая А на Eij |
слева, мы прибавляем к i-й |
||
строке j-ю, умноженную на , а умножая А на Eij справа, мы прибавляем к j-му столбцу i-й, умноженный на . Заметим, что обратная к элементарной матрице
1
тоже элементарная, а именно, Eij Eij (упр. 4.7).
Любую невырожденную матрицу Mn можно привести к виду
Mn E1E2...EkDEk 1...Es ,
где Em – элементарные, а D – диагональная матрица. Такое представление не
однозначно. В зависимости от решаемой задачи матрицу можно представить так, чтобы элементарные матрицы были только слева или только справа от диагональной. Используя представление матрицы в виде произведения элементарных и диагональной, можно решать матричные уравнения. А именно,
AX B E1E2...EsDX B X D 1 Es 1... E2 1 E1 1 B.
Если интерпретировать эти действия с точки зрения элементарных преобразований, то это означает, что для решения матричного уравнения можно использовать следующий способ:
1)записываем матрицы A,B в виде расширенной матрицы A B ;
2)приводим матрицу A к диагональному виду элементарными преобразованиями строк, изменяя при этом и матрицу В:
A |
|
B |
Es 1... E2 |
1 E1 |
1 E1E2...EsD |
Es 1... E2 1 E1 1 B; |
|
||||||
|
|
|
|
|
|
|
|
|
|
A |
|
||
|
|
|
|
D |
|
|
3)делим строки на соответствующие диагональные элементы матрицы D (это эквивалентно умножению на D 1). В результате слева получится единичная матрица:
21

E |
|
D 1 |
Es 1 |
... E2 |
1 E1 1 B; |
|
|||||
|
|
|
|||
|
|
|
|
A 1 |
|
4) полученная в правой части матрица A 1B и есть решение уравнения AX B.
Замечание. Описанный выше метод можно схематично представить в следующем виде: A B E X . Для решения уравнения XA B к единичному
виду следует привести матрицу |
A в записи |
A |
с помощью элементарных |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
B |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
A |
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
преобразований столбцов: |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
B |
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
3 |
|
|
|
1 |
1 |
1 |
|
|
|
|
|||||||||||||
|
|
Пример 2. Решить уравнение |
|
8 |
|
6 |
9 |
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
X |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
8 |
2 |
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Решение. Обозначим i-ю сторку матрицы как ai . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
3 |
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 6 9 |
|
B |
|
0 0 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
A |
, |
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
8 |
|
|
2 |
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
4 2 3 |
|
1 1 1 |
|
|
|
a 2a |
|
|
|
4 2 |
3 |
|
1 1 1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
A |
|
B E |
|
X |
|
8 6 9 |
|
0 0 0 |
|
|
|
|
a2 |
a 1 |
|
|
|
0 2 |
3 |
|
2 2 2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 8 2 |
|
0 0 0 |
|
|
|
|
|
|
|
|
|
|
0 6 1 |
|
1 1 1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a1 a2 |
4 0 0 |
|
3 3 |
|
|
3 |
|
|
a2 0,5a3 |
4 0 0 |
|
|
3 |
|
|
3 |
3 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
a3 3a2 |
|
0 2 |
3 |
|
|
2 2 |
|
|
2 |
|
|
|
|
0 |
2 |
|
0 |
|
|
0,5 |
0,5 |
0,5 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
0 0 6 |
|
5 5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
0 0 6 |
|
5 |
5 |
5 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
a1:4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
3/4 |
|
|
3/4 |
|
|
3/4 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a2:2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
a :( 6) |
|
|
|
0 1 0 |
|
1/4 |
|
|
1/4 |
|
|
1/4 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
1 |
5/6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5/6 5/6 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3/4 |
|
3/4 |
|
|
|
3/4 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/4 |
|
|
1/4 |
|
|
1/4 |
|
|
|
|
|
|
|
|
█ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5/6 |
|
5/6 |
5/6 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4 |
2 |
3 |
|
1 |
1 |
1 |
||||
Пример 3. Решить уравнение X |
|
8 |
6 |
9 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
||||||||
|
|
4 |
8 |
2 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
||||||
Решение. Обозначим j-й столбец матрицы как aj .
|
A |
|
E |
||
|
|
|
|
|
|
|
|
||||
|
B |
|
X |
||
|
4 |
2 |
3 |
|
|
|
1 |
1 |
1 |
|
||
A |
|
8 6 9 |
|
, |
B |
|
0 0 0 |
|
||||
|
|
|
. |
|||||||||
|
|
4 |
8 |
2 |
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
||||||
|
4 |
2 |
3 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
8 6 |
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
|
|
9 |
|
a1:4 |
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
:2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
8 |
2 |
|
a |
|
|
1 |
|
|
4 |
|
|
|
2/3 |
a |
a |
|
|
|
|
||||||||
|
|
a3:3 |
|
|
|
|
|
|
a3 |
a1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 1 |
|
|
|
|
1/2 |
|
|
1/3 |
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
1/4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
0 |
0 |
0 |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
||
|
2 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||
|
1 |
|
|
3 |
1/3 |
a 2a |
|
|
5 |
|
|
|
3 |
10/3 |
|
||||||||||||||
|
|
|
|
|
|
a3 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
a3 a2 |
|
|
|
|
|
10 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1/4 |
1/4 |
1/12 |
|
|
|
|
|
|
1/4 |
|
1/4 |
1/6 |
|
|
|
|
|||||||||||||
|
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
||
|
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
0 |
|
|
|
0 |
|
|
|
|
|
|
1 |
0 |
|
0 |
|
|
|
|
|
||||||
|
|
|
0 |
1 |
|
|
|
0 |
|
|
|
|
|
|
|
0 |
1 |
|
0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
||||||||||||
|
|
5 |
3 |
|
|
|
1 |
a 5a |
|
0 |
0 |
|
|
1 |
|
|
|
||||||||||||
|
|
|
|
|
a2 |
3a3 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||
|
|
1/4 |
|
|
|
0 |
1/10 |
1/20 |
|
|
|
||||||||||||||||||
|
|
1/4 |
1/20 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
0 |
0 |
|
0 |
|
|
|
|
|
||||||
|
|
|
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
1/10 1/20 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
X |
|
0 |
0 |
|
|
0 |
|
|
. |
|
|
|
|
|
|
|
|
█ |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Упражнения и задачи.
4.1.Доказать, что  n, ,
n, ,  , где n , – коммутативное и ассоциативное кольцо с единицей.
, где n , – коммутативное и ассоциативное кольцо с единицей.
4.2.Доказать, что, если p – простое число, то 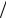 p, ,
p, , 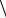 – поле.
– поле.
4.3.Составить таблицы Кэли для операций сложения и умножения в полях вычетов:
а)  2, ,
2, ,  ; б)
; б)  3, ,
3, ,  ;
;
в)  5, ,
5, ,  .
.
4.4.Решить систему линейных уравнений в поле вычетов F5 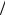 5, ,
5, ,  :
:
3x 4y z 2,
а) 2x 4z 1,
y 2z 0;
x 2y 3z 1,
б) 2x z 0,y 2z 4;
2x 2y z 1,
в) x 2z 0,y 3z 1.
4.5.Доказать, что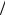 Mn( ), ,
Mn( ), ,  – ассоциативное кольцо с единицей.
– ассоциативное кольцо с единицей.
4.6.Доказать, что умножение матрицы A на элементарную матрицу Eij слева и справа равносильно элементарным преобразованиям матрицы A:
а) Eij A– прибавлению к i-й строке матрицы A j-й строки матрицы A,
умноженной на ;
б) AEij – прибавлению к j-му столбцу матрицы A i-го столбца матрицы A,
умноженного на .
24
1
4.7. Доказать, что Eij Eij .
4.8.Решить уравнение AX B, если
а) A |
1 |
1 |
|
B |
0 |
|
1 |
|
|
|
|||||
|
2 |
0 |
, |
|
|
|
|
|
; |
|
|
|
|||
|
|
|
|
|
|
2 |
|
1 |
|
|
|
||||
|
0 |
5 |
, |
|
|
5 |
|
5 |
|
|
|
|
|||
б) A |
5 |
|
|
B |
5 |
|
|
. |
|
|
|
||||
|
|
5 |
|
|
|
|
|
0 |
|
|
|
|
|||
|
1 |
0 |
1 |
|
|
|
3 |
|
0 1 |
||||||
в) A |
|
|
1 1 |
|
, B |
|
|
0 |
|
1 0 |
|
||||
1 |
|
|
|
|
; |
||||||||||
|
|
|
1 |
0 |
|
|
|
|
|
0 |
|
0 |
4 |
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
4 |
7 |
3 |
|
|
|
|
0 |
0 |
4 |
|||||
г) A |
|
2 1 0 |
|
B |
|
1 |
1 1 |
|
|||||||
|
, |
|
. |
||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
1 0 |
|
||
|
|
1 1 |
|
|
|
|
|
||||||||
4.9.Решить уравнение XA B, если
а) A |
1 |
1 |
|
B |
0 |
|
1 |
|
|
|
|||||
|
2 |
0 |
, |
|
|
|
|
|
; |
|
|
|
|||
|
|
|
|
|
|
2 |
|
1 |
|
|
|
||||
|
0 |
5 |
, |
|
|
5 |
|
5 |
|
|
|
|
|||
б) A |
5 |
|
|
B |
5 |
|
|
. |
|
|
|
||||
|
|
5 |
|
|
|
|
|
0 |
|
|
|
|
|||
|
1 |
0 |
1 |
|
|
|
3 |
|
0 1 |
||||||
в) A |
|
|
1 1 |
|
, B |
|
|
0 |
|
1 0 |
|
||||
1 |
|
|
|
|
; |
||||||||||
|
|
|
1 |
0 |
|
|
|
|
|
0 |
|
0 |
4 |
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
4 |
7 |
3 |
|
|
|
|
0 |
0 |
4 |
|||||
г) A |
|
2 1 0 |
|
B |
|
1 |
1 1 |
|
|||||||
|
, |
|
. |
||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
1 0 |
|
||
|
|
1 1 |
|
|
|
|
|
||||||||
25

5. Евклидовы кольца. Кольцо многочленов над полем
Норма – это функция :M , которая ставит в соответствие каждому элементу а некоторого кольца  M, ,
M, ,  число (а) и такая, что:
число (а) и такая, что:
1) (ab) (a) |
a,b 0; |
|
r 0 (r) (b) . |
|
2) a,b A, b 0 |
q A: |
a bq r, |
||
Например, если рассмотреть кольцо целых чисел, то в качестве нормы можно взять модуль числа (проверить аксиомы нормы предлагается самостоятельно).
Норма позволяет ввести в кольце процедуру деления с остатком.
Если r = 0, то говорят, что a делится на b a b или b делит a (b | a).
Наибольшим общим делителем (НОД) элементов кольца a и b
называется такой элемент кольца d, который делит и a, и b, при этом любой другой элемент с таким свойством обязательно делит d.
Если НОД(a,b)=1, то a и b взаимно простые.
Наименьшим общим кратным (НОК) элементов кольца a и b
называется такой элемент кольца c, который делится и на a, и на b, при этом любой другой элемент с таким свойством обязательно делится на c. Если a и b взаимно просты, то НОК(a,b)= a×b. В общем случае, если НОК(a,b)= d, то НОК(a,b)= a×b:НОД(a,b).
Евклидово кольцо – это кольцо, в котором определено деление с
остатком. |
|
|
|
Примером евклидова кольца является кольцо x , , |
многочленов |
||
Pn(x) с вещественными коэффициентами: |
|
|
|
n |
|
|
|
Pn(x) x Pn(x) ak xk, |
ak , |
an 0. |
|
k 0 |
|
|
|
Значение n называется степенью многочлена Pn(x) и |
является его |
||
нормой (упр. 5.1). |
|
|
|
Алгоритм деления многочленов подобен алгоритму деления чисел «уголком».
Пример 1. Представить в виде суммы целой части и правильной дроби (т.е. рациональной дроби, у которой степень многочлена в числителе строго
меньше степени многочлена в знаменателе) рациональную дробь 3x3 4x2 2 . x2 1
Решение. |
|
|
|
|
|
3x3 |
4x2 |
2 |
|
x2 1 |
|
|
|||||
Шаг 1: |
|
|
|
|
|
|
|
|
3x |
||
3x3 3x |
|
|
|||
26

3x3 |
4x2 |
2 |
x2 1 |
|
|
|
|
|
|
|
|
3x 4 |
||
3x3 3x |
|
|||
Шаг 2:
4x2 3x 24x2 4
|
|
3x3 4x2 |
2 |
|
x2 1 |
|
||||||
|
3x3 3x |
|
|
|
3x 4 |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Шаг 3: |
|
4x2 3x 2 |
|
|
|
|
|
|
||||
|
4x2 4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 2 |
|
|
|
|
|
|
|
|
|
|
3x3 4x2 2 |
|
|
|
|
3x 2 |
|
|||||
Следовательно, |
|
|
|
3x |
4 |
|
|
. |
█ |
|||
|
|
|
x2 |
|
||||||||
|
|
x2 1 |
|
|
|
|
1 |
|
||||
Алгоритм Евклида (нахождение НОД(a,b)).
1)Разделим с остатком a на b: a qb r.
2)Если r не равен 0, то разделим b на r: b q1r r1.
3)Если r1 не равен 0, то разделим r на r1:
rq2r1 r2 .
4)Если r2 не равен 0, то разделим r1 на r2 :
r1 q3r2 r3.
…
i) Если ri не равен 0, то разделим ri 1 на ri :
ri 1 qi 1ri ri 1.
Продолжаем процедуру деления, до последнего ненулевого остатка rn :
|
rn 1 qn 1rn |
|
НОД(a,b) rn. |
Пример 2. |
Найти НОД f (x),g(x) и НОК f (x),g(x) многочленов |
||
f (x) 3x4 15x2 12, g(x) x3 x2 x 1 над полем |
|||
а) , , ; |
б) F5, , . |
|
|
|
|
27 |
|

Решение.
а) Используем алгоритм Евклида.
Шаг 1. |
|
|
|
Шаг 2. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
3x4 15x2 12 |
|
x3 x2 x 1 |
|
|
|
x |
3 |
x |
2 |
x 1 |
|
9x |
2 |
9 |
||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
3x4 3x3 3x2 3x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3x 3 |
3 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x |
x |
|
|
|
1/9x 1/9 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3x3 12x2 3x 12 |
|
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
||||||||
|
3x3 3x2 3x 3 |
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
9x2 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Над полем  , ,
, ,  НОД f (x),g(x) =x2 1.
НОД f (x),g(x) =x2 1.
Замечание. Обратите внимание, что вместо 9x2 9 в качестве НОД мы
выбрали |
x2 1. А могли взять |
3x2 3 и вообще любой многочлен вида |
k x2 1 , |
где k (проверьте). |
Но, чтобы избежать неоднозначности, в |
качестве НОД двух многочленов всегда берётся тот, старший коэффициент которого равен 1.
|
|
|
|
|
4 |
|
2 |
2 |
1 |
|
|
|
|
|
|||
|
|
|
|
|
3x 15x 12 |
x |
|
|
|
|
|
||||||
|
|
|
|
|
4 |
|
2 |
2 |
|
|
|
|
|
|
|
||
|
f(x) |
|
|
3x |
3x |
3x |
12 |
|
|
|
|
||||||
НОК f (x),g(x) = |
|
|
|
|
|
|
|
|
|
2 |
3 |
2 |
|
||||
|
|
g(x) |
|
12x2 12 |
|
|
|
|
(3x |
12)(x |
x |
x 1) |
|||||
2 |
|
|
|
|
|||||||||||||
|
x 1 |
|
|
|
|
2 |
12 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
12x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3x5 3x4 15x3 15x2 12x 12.
б) Пересчитаем коэффициенты многочленов в поле вычетов по модулю 5:
f (x) 3x4 2, g(x) x3 4x2 4x 1.
Применим алгоритм Евклида, выполняя все операции в поле вычетов  F5, ,
F5, ,  :
:
Шаг 1. |
|
|
|
Шаг 2. |
|
|
||||
|
|
3x4 2 |
|
x3 4x2 4x 1 |
|
|
x3 4x2 4x 1 |
|
x2 4 |
|
|
|
|
|
|||||||
|
|
3x4 2x3 2x2 3x |
|
3x 3 |
|
|
|
x3 4x |
|
x 4 |
|
|
|
|
|
|
|||||
|
|
3x3 3x2 2x 2 |
|
|
|
|
|
4x2 1 |
|
|
|
|
3x3 2x2 2x 3 |
|
|
|
|
|
4x2 1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 4 |
|
|
|
0 |
|
|
||
|
|
|
28 |
|
|
|
|
|
||

Над полем F , , |
НОД f (x),g(x) =x2 4; |
|
|
|
|
|||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
3x |
|
|
x |
4 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||
НОК f (x),g(x) = |
|
f(x) |
|
3x |
2x |
3x 3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
2 |
|
|||
|
|
|
g(x) |
|
|
3x2 2 |
|
|
|
|
|
(3x |
3)(x |
4x |
4x 1) |
|||
|
2 |
|
|
|
|
|||||||||||||
|
|
x 4 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3x5 2x4 2x 3. █
Упражнения и задачи
5.1.Доказать, что в кольце 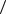 x , ,
x , , 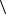 в качестве нормы многочлена можно взять его степень.
в качестве нормы многочлена можно взять его степень.
5.2. Найти НОД f (x),g(x) и НОК f (x),g(x) многочленов
f (x) x3 2x2 2x 1, |
g(x) x2 |
2x 1 над полем , , . |
|
5.3. Найти НОД f (x),g(x) и НОК f (x),g(x) многочленов |
|||
|
f (x) 5x3 x2 5x 1, |
g(x) 5x2 21x 4 над полем |
|
а) |
, , ; |
|
|
б) |
F3, , ; |
|
|
в) |
F5, , . |
|
|
5.4. Найти НОД f (x),g(x) и НОК f (x),g(x) многочленов
f (x) x4 1, g(x) x3 x 1 над полем
а)  , ,
, ,  ;
;
б)  F3, ,
F3, ,  ;
;
в)  F5, ,
F5, ,  .
.
5.5. Найти НОД f (x),g(x) и НОК f (x),g(x) многочленов
f (x) x7 8x3 9, g(x) x4 5x 6 над полем
а)  , ,
, ,  ;
;
б)  F3, ,
F3, ,  ;
;
в)  F5, ,
F5, ,  .
.
29
6. Линейное пространство. Линейная зависимость векторов
Линейное (векторное) пространство U над полем F  M, ,
M, ,  с
с
бинарной операцией
:U2 U (сложение элементов пространства)
U
иунарными операциями, определенными для каждого числа из поля
:U U (умножение вектора на скаляр)
определяется следующими аксиомами:
1) |
u |
, |
v |
, |
w |
U |
( |
u |
|
v |
) |
w |
|
u |
( |
v |
|
w |
) U ; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
U U |
|
|
|
|
|
U U |
||||||||||||
2) |
|
U : |
|
u |
U |
u |
|
|
|
|
|
u |
|
u |
; |
||||||||||||||
0 |
0 |
0 |
|||||||||||||||||||||||||||
UU
3)u U u U : u ( u) ( u) u 0;
UU
4)u,v U u v v u U ;
U U
5) F u,v U (u v) u v U ;
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
U |
||||||
6) , F |
|
u |
U ( |
u |
) ( ) |
u |
; |
|
|
||||||||||||
7) , F |
|
u |
U ( ) |
u |
|
u |
|
u |
; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
||||
8) |
u |
U, 1 F |
|
|
|
1 |
u |
|
u |
. |
|
|
|
|
|
|
|
|
|
|
|
Условия 1) – 4) означают, что  U,
U,  – абелева группа. Условия 5) – 8) задают
– абелева группа. Условия 5) – 8) задают
U
свойства умножения элементов пространства на число из поля. Элементы линейного пространства называются векторами.
Замечание. Символ умножения на число из поля обычно пропускают.
Примерами |
|
линейного |
пространства |
являются |
|
пространство |
|||||
3направленных |
отрезков; пространство n строк длины |
n; пространство |
|||||||||
многочленов x . |
|
|
|
|
|
|
|||||
Линейной |
комбинацией |
системы векторов |
u1, |
u |
2,..., |
u |
k U называется |
||||
сумма 1 |
u1 2 |
u |
2 ... k |
u |
k U , 1, 2,..., k F . |
Элементы поля 1, 2,..., k |
|||||
при этом называются коэффициентами линейной комбинации. Тривиальная линейная комбинация – это линейная комбинация, все коэффициенты которой равны 0.
30
