
656_Lytkina_D.V._Algebraicheskie_struktury_
.pdf
13. Самосопряженные операторы. Ортогональные операторы. Полярное разложение матрицы линейного оператора
Пусть φ – линейный оператор эвклидова пространства с матрицей A(φ).
Сопряженный к линейному оператору φ оператор φ* – это линейный оператор, удовлетворяющий условию
x,y U (x) y x *(y).
Самосопряженный (симметрический) оператор – это линейный оператор, который совпадает с сопряженным к нему оператором: *(x) (x).
Матрица самосопряженного оператора в любом ортонормированном базисе симметрична (упр. 13.5), а все собственные значения самосопряженного оператора – действительные числа (упр. 13.7). Следовательно, матрица самосопряженного оператора всегда может быть приведена к жордановой форме над полем вещественных чисел.
Ортогональный оператор – это линейный оператор, обратный которому совпадает с сопряженным к нему: *(x) 1(x). Матрица ортогонального оператора в ортонормированном базисе обладает замечательным свойством:
AОНБ ( ) 1 AОНБ( ) T .
Полярное разложение матрицы линейного оператора евклидова пространства – это представление матрицы этого оператора в виде произведения матриц ортогонального и самосопряженного операторов: A US .
Метод полярного разложения матрицы линейного оператора. Найдем произведение матрицы оператора на транспонированную: AT A. Полученная матрица симметрична и соответствует некоторому самосопряженному оператору (упр. 13.5). В ортонормированном базисе из собственных векторов матрица AT A имеет диагональный вид (упр. 13.8):
TB ОНБ AT A TОНБ B D i ,
где диагональные элементы – собственные значения матрицы.
Из диагональной матрицы без труда извлекается квадратный корень:
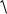
 AT A ОНБ
AT A ОНБ 
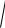 D i D
D i D
 i .
i .
Возвращая D i в исходный базис, получаем «симметричный» сомножитель в полярном разложении:
S : 
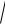 AT A B TB ОНБ 1 D
AT A B TB ОНБ 1 D
 i TB ОНБ .
i TB ОНБ .
Полезно учесть, что TB ОНБ 1 TB ОНБ T .
71

В качестве «ортогонального» сомножителя полярного разложения возьмем матрицу U AS 1:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
A A |
|
AT A |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AT A. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
||
|
|
Пример. Найти полярное разложение матрицы A |
2 |
. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||
|
|
Решение. Найдем транспонированную матрицу и умножим ее на |
|||||||||||||||||||||||||||||||||||||
исходную слева: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
1 |
|
4 |
, |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
AT A |
17 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
||||||
Найдем собственные числа и собственные векторы матрицы AT A: |
|
||||||||||||||||||||||||||||||||||||||
|
AT A E |
|
|
|
17 |
|
6 |
|
2 25 100 0, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
6 |
8 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
5, 2 20; |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12 |
6 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
|
y 2x |
u |
o |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
6 |
3 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
6 x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
o |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x 2y |
v |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
6 |
12 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вычислим матрицу |
|
AT A |
|
в ортонормированном |
базисе |
из |
собственных |
||||||||||||||||||||||||||||||||
векторов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
AT A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ОНБ |
0 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
||||||||||||
Найдем матрицы перехода в ортонормированный базис и из ортонормированного базиса:
72
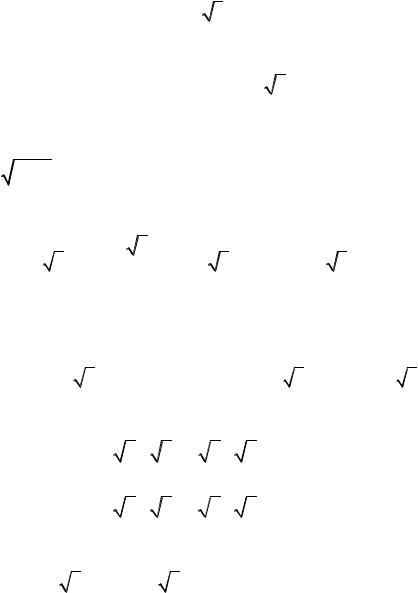
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОНБ B |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
T |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B ОНБ |
|
|
|
|
|
|
ОНБ B |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Найдем «симметрическую» часть полярного разложения: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S TОНБ B |
|
|
|
|
|
|
TОНБ B 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
AT A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ОНБ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 1 2 |
|
|
1 |
|
|
|
0 1 1 2 |
|
|
|
1 9 2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
5 |
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 6 |
|
, |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Найдем «ортогональную» часть полярного разложения: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
2 1 9 2 1 |
|
|
|
1 |
|
|
|
|
2 1 |
|
6 2 |
|
|
1 1 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
U AS 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
||||||||||||||||||||||||||||||||||||||||||
4 |
|
2 |
|
|
|
5 2 6 |
|
|
|
|
|
|
|
|
|
|
|
|
2 10 5 |
|
2 9 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
9 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Следовательно, |
A US |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
2 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Проверка: A US |
|
|
|
|
1 1 2 1 9 2 |
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
█ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 2 1 |
|
2 6 |
|
|
|
4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
73

Упражнения и задачи
13.1.Доказать, что ( ) * *( *).
13.2.Доказать, что * * .
13.3.Доказать, что 1 * * 1.
13.4.Доказать, что в любом ортонормированном базисе AB * ABT .
13.5.Доказать, что матрица самосопряженного оператора в любом ортонормированном базисе симметрична.
13.6.Доказать, что собственные векторы самосопряженного оператора, соответствующие различным собственным значениям, ортогональны.
13.7.Доказать, что все собственные значения самосопряженного оператора – вещественные числа.
13.8.Доказать, что матрица самосопряженного оператора диагонализируема.
13.9.Доказать, что определитель матрицы ортогонального оператора в любом базисе равен +1 или -1.
13.10.Доказать, что для ортогонального оператора верно равенство
xy (x) (y), x,y U .
13.11.Найти полярное разложение матрицы
|
3 |
1 |
|
|
|
а) A |
1 |
; |
|
||
|
|
3 |
|
|
|
|
3 |
3 |
; |
|
|
б) A |
1 |
|
|
||
|
|
1 |
|
|
|
в) |
2 |
2 |
; |
|
|
A |
3 |
|
|
||
|
|
3 |
|
|
|
г) |
1 |
2 |
; |
||
A |
4 |
2 |
|
||
|
|
|
|
||
|
1 |
1 |
|
|
|
д) A |
|
; |
|
|
|
|
1 |
0 |
|
|
|
|
0 |
1 |
|
|
|
е) A |
1 |
. |
|
|
|
|
|
1 |
|
|
|
74
13.12. Найти полярное разложение матрицы, сделать проверку.
|
4 |
2 |
|
2 |
|
|||
а) A |
|
4 |
|
|
|
|
|
; |
|
4 1 |
|||||||
|
|
2 |
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
1 |
1 |
0 |
|
|
|
||
б) A |
|
0 |
1 |
1 |
|
; |
|
|
|
|
|
|
|||||
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
1 |
1 |
|
|
|
||
в) A |
|
0 |
1 |
|
|
|
|
|
|
1 . |
|
|
|||||
|
|
0 |
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|||
75
14. Билинейная форма. Квадратичная форма
Билинейная форма – это функция двух аргументов из линейного пространства (над полем действительных чисел) со значениями во множестве действительных чисел, которая является линейной по каждому аргументу:
|
|
|
|
|
|
|
|
f :U U , |
|||||||||||||||||
|
x |
, |
y |
, |
z |
U, |
, |
f ( |
x |
|
y |
, |
z |
) f ( |
x |
, |
z |
) f ( |
y |
, |
z |
), |
|||
|
x |
, |
y |
, |
z |
U, |
, |
f ( |
x |
, |
y |
z) f ( |
x |
, |
y |
) f ( |
x |
, |
z |
). |
|||||
Если каждый из векторов-аргументов билинейной формы представить в виде разложения по некоторому фиксированному базису B {e1,e2,...,en} в U, то из определения билинейной формы следует, что
|
n |
|
n |
||
x |
i |
ei, |
y |
i |
ei , |
|
i 1 |
|
i 1 |
||
f ( |
x |
, |
y |
) f |
|
|
e |
, |
|
|
j |
e |
|
|
|
j |
f ( |
e |
, |
e |
). |
|
|
|
|
|
i i |
|
|
j |
i |
|
i j |
|
|||||||||
|
|
|
|
1 i n |
|
|
|
1 j n |
|
|
|
|
1 i n |
|
|
|
|
|
|
|
|
1 j n
Назовем матрицу FB , составленную из значений билинейной формы на базисных векторах, матрицей билинейной формы в базисе B:
FB FB ij i |
|
, |
FB ij f ( |
|
|
|
i |
|
, j |
|
, |
|
ei, |
e |
j), |
1,n |
1,n |
||||||
1,n |
|||||||||||
j 1,n |
|
|
|
|
|
|
|
|
|
||
Тогда билинейная форма может быть записана в матричном виде:
f (x,y) x B FB y B .
При переходе из базиса B пространства U в базис B' с матрицей перехода TB B' матрица билинейной формы меняется согласно следующей формуле:
f ( |
x |
, |
y |
) |
x |
|
|
FB |
y |
B |
|
|
|
x |
|
|
FB |
|
y |
B' |
|
x |
|
|
TB B' T FBTB B' |
y |
B' |
||
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
B' |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
x |
B' TB B' T |
TB B' |
y |
B' |
|
|
|
|
FB' |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
F |
T |
|
T F T |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
B' |
|
B B' |
|
|
|
B |
B B' |
|
|
|
|
|
||||
Симметричная билинейная форма – это форма, не изменяющаяся при перестановке аргументов, т.е. f (x,y) f (y,x).
Замечание. Скалярное произведение является билинейной формой с матрицей Грама в качестве матрицы билинейной формы.
76

Квадратичная форма – это билинейная форма от одинаковых аргументов:
(x) f (x,x) x B FB x B .
При этом говорят, что билинейная форма f (x,x) порождает квадратичную форму (x).
Замечание. Симметричная билинейная форма может быть восстановлена по порожденной ею квадратичной форме:
f (x,y) 1 (x y) (x y) , 4
f (x,y) 1 (x y) (x) (y) . 2
Матрица квадратичной формы – это матрица порождающей ее симметричной билинейной формы.
Если квадратичная форма задана в виде уравнения
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( |
|
) aiixi2 2 |
aijxi xj, |
aij , |
i, j |
|
|
, |
|||||||||||
x |
1,n |
||||||||||||||||||
|
|
i 1 |
|
|
|
|
1 i j n |
|
|
|
|
|
|
|
|
|
|||
то ее матрица имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a |
a12 |
|
a1n |
|
|
|
|
|
|
||||||||
|
|
|
11 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
a2n |
|
|
|
|
|
|
|||||
|
|
|
|
a12 |
|
|
a |
|
|
|
|
|
|
|
|
||||
A |
2 |
|
|
|
22 |
|
2 |
|
, |
a , |
i, j |
1,n |
. |
||||||
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
a2n |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
a1n |
|
|
a |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
nn |
|
|
|
|
|
|
|
|
|||
Матрица квадратичной формы симметрична и поэтому соответствует некоторому самосопряженному оператору линейного пространства. Можно доказать (упр. 14.5), что существует ортонормированный базис из собственных векторов (канонический базис) в котором матрица квадратичной формы имеет диагональный (канонический) вид.
Пример. Привести квадратичную форму x 14x2 24xy 21y2
y
к каноническому виду. |
|
14 |
12 |
Решение. Запишем матрицу квадратичной формы: A |
. |
12 |
21 |
77 |
|

Найдем собственные значения и собственные векторы:
|
A E |
|
|
14 |
|
12 |
|
2 |
35 150 0, 30, |
|
|
|
5 |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
12 |
21 |
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||
|
|
|
|
|
|
16 |
12 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
30 |
|
|
|
0 |
|
4x 3y |
|
u |
|
5 |
|
||||||||||||||||||
|
|
|
|
; |
|||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|||||||||
|
|
|
|
|
|
12 |
|
9 y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5 |
|
|
|
|
9 |
12 x |
0 |
|
3x 4y |
|
u |
|
|
|
|
|
|
5 |
|
||||||||||
|
|
|
2 |
|
|
|
. |
||||||||||||||||||||||
2 |
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||
|
|
|
|
|
|
12 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В базисе u1,u2 квадратичная форма имеет канонический вид:
|
x' |
30 x' 2 |
5 y' 2. |
|
|
ОНБ |
|
|
|
|
y' |
|
|
|
Найдем зависимость между «старыми» и «новыми» переменными.
Запишем матрицы перехода к каноническому базису:
T |
|
|
|
1 3 4 |
|
, |
|
T |
|
|
|
1 |
3 4 |
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
B ОНБ |
|
|
|
|
|
|
|
ОНБ B |
|
|
5 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
5 4 3 |
|
|
|
|
|
|
|
|
|
4 3 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 4y |
|
|
|
|
|
|
||
x' |
|
|
|
|
x |
|
|
1 3 |
4 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
T |
|
|
|
|
|
5 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
; |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
B ОНБ |
|
5 |
4 3 |
|
|
4x 3y |
|
|
|||||||||||||||||||||
y' |
|
|
|
|
y |
|
|
y |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x' 4y' |
|
|
|||||||||
x T |
|
|
x' |
|
1 3 4 x' |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
5 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
ОНБ B |
|
5 |
|
4 |
3 |
|
|
|
4x' 3y' |
|
|
||||||||||||||||
y |
|
|
|
|
|
y' |
|
|
|
|
y' |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
14x2 |
24xy 21y2 |
|
3x 4y 2 |
4x 3y 2 |
|||||||||||||||||||||||||
Таким образом, |
|
|
30 |
|
|
|
|
|
|
|
5 |
|
|
|
. █ |
|||||||||||||||
|
|
|
5 |
|
|
|
5 |
|||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Закон инерции. Количество положительных, отрицательных и нулевых коэффициентов в каноническом виде квадратичной формы в различных базисах постоянно.
78
Упражнения и задачи
14.1.Доказать, что матрица симметричной билинейной формой симметрична в любом базисе.
14.2.Доказать, что если в некотором базисе матрица билинейной формы симметрична, то билинейная форма симметрична.
14.3.Доказать, что различные билинейные формы могут порождать одну и ту же квадратичную форму.
14.4.Доказать, что две билинейные формы f и g порождают одну и ту же квадратичную форму, если f (x,y) f (y,x) g(x,y) g(y,x).
14.5.Доказать, что существует базис, в котором матрица любой симметричной билинейной формы имеет диагональный вид.
14.6.Приведите следующие квадратичные формы к каноническому виду:
а) (x,y) 8x2 12xy 8y2 ;
б) (x,y) 3x2 8xy 3y2;
в) (x,y) 7x2 3xy 3y2;
г) (x,y) 17x2 12xy 8y2;
д) (x,y) 6x2 4xy 9y2 ;
е) (x,y) 15x2 20xy 63y2 ;
ж) (x,y) 25x2 120xy 313y2 ;
з) (x,y) x2 6xy 9y2;
и) (x,y) x2 4xy 4y2 ;
к) (x,y) 4x2 4xy y2;
л) (x,y) x2 10xy 25y2;
м) (x,y) 6x2 4xy 9y2 .
14.7.Приведите квадратичные формы к каноническому виду:
а) (x,y,z) x2 2xy 5y2 4z2 4xz;
б) (x,y,z) 4x2 4xy y2 z2 4xz 3yz;
в) (x,y,z) xy xz yz.
79

15. Кривые второго порядка
Кривая второго порядка – это геометрическое место точек, координаты которых удовлетворяют общему уравнению
a11x2 a12xy a22y2 a1x a2y a0 0.
Общее уравнение кривой второго порядка можно записать в матричном
виде:
a11
x y
a12
2
a12 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|||
2 |
a |
a |
|
a 0. |
||||||
|
||||||||||
|
|
|
|
1 |
2 |
|
|
|
0 |
|
a |
y |
|
|
|
y |
|
||||
|
|
|
|
|
|
|
|
|
||
22 |
|
|
|
|
|
|
|
|
|
|
Первое слагаемое представляет собой квадратичную форму, матрица которой в ортонормированном базисе из собственных векторов имеет канонический (диагональный) вид:
x |
1 |
0 |
x |
a1 |
x |
|
|
||||
y TB ОНБ |
0 |
|
TОНБ B y |
|
a2 y |
|
a0 |
0. |
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
Для самосопряженного оператора матрица перехода в ортонормированный базис является ортогональной, а значит,
TB ОНБ TОНБ1 B TОНБT B .
Зная матрицу перехода к ортонормированному базису TB ОНБ , уравнение кривой второго порядка можно преобразовать:
x |
|
|
|
y TB ОНБ |
1 |
||
|
|
0 |
|
|
x' y' |
|
|
T
0 |
x |
y TT |
|
a |
a x a 0, |
|
2 |
|
|
1 |
y |
0 |
|
|
|
ОНБ B |
|
2 |
||
|
|
TB ОНБ |
|
|
|
|
x' |
y' |
1 |
0 x' |
a |
a |
T |
T |
|
x |
a 0, |
||||
|
|
|
|
|
|
1 |
2 |
|
B ОНБ |
|
ОНБ B |
0 |
||
|
|
|
0 |
2 y' |
|
|
|
|
y |
|
||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
x' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
' |
|
|
x' 2 |
y' 2 x' |
y' a |
0, где |
x' |
T |
x . |
|||||||
1 |
|
|
2 |
|
1 |
2 |
|
0 |
|
|
|
|
B ОНБ |
|
|
|
|
|
|
|
|
|
|
|
|
y' |
|
y |
|
Последнее уравнение может быть преобразовано в двух случая:
80
