
656_Lytkina_D.V._Algebraicheskie_struktury_
.pdf
1)при ненулевых коэффициентах 1, 2 можно выделить полные квадраты и привести равенство к виду 1 x' x0 2 2 y' y0 2 c 0;
2)при только одном ненулевом коэффициенте, допустим, 1 0 равенство приводится к виду 1 x' x0 2 y' y0 2 0.
«Новые» переменные x'',y'' являются линейным преобразованием
«старых» x,y , а именно, получены в результате поворота и параллельного переноса системы координат.
Каноническим уравнением кривой второго порядка называется уравнение, приведенное к виду:
|
x' x |
2 |
y' y |
2 c 0 |
или |
x' x |
|
y' y |
2 0. |
1 |
0 |
2 |
0 |
|
1 |
0 |
2 |
0 |
|
Нормальной формой уравнения кривой второго порядка называется каноническое уравнение, в котором коэффициенты перед полными квадратами равны 1.
Замечание. Собственные векторы матрицы размера 2х2, а следовательно, и матрицы перехода к базису из собственных векторов можно всегда подобрать
так, |
чтобы |
выполнялось |
равенство |
TB ОНБ TОНБ B . |
Корни |
характеристического многочлена в случае a12 0 являются различными вещественными числами, следовательно, собственные векторы ортогональны (упр. 13.6 и 13.7) и могут быть выбраны в виде пары
|
a |
|
|
|
b |
|
|
|
|
|
|
u1 |
, |
u |
2 |
|
, |
u1 |
|
u |
2 |
1. |
|
|
b |
|
|
|
a |
|
|
|
|
|
|
Тогда для матрицы перехода имеют место равенства:
a |
b |
, |
TОНБ B |
|
|
b |
a |
|
T |
T 1 |
TT |
|
a |
b |
T |
. |
B ОНБ |
ОНБ B |
ОНБ B |
|
|
|
ОНБ B |
|
|
|
|
|
b |
a |
|
|
Кривые второго порядка разбиваются на несколько типов в зависимости от знаков коэффициентов канонического уравнения. Все невырожденные варианты сводятся к трем случаям:
|
x x |
2 |
y y |
o |
2 |
|||
1) |
|
o |
|
|
|
|
1, эллипс (рис. 1а); |
|
a |
2 |
|
b2 |
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
81 |
|
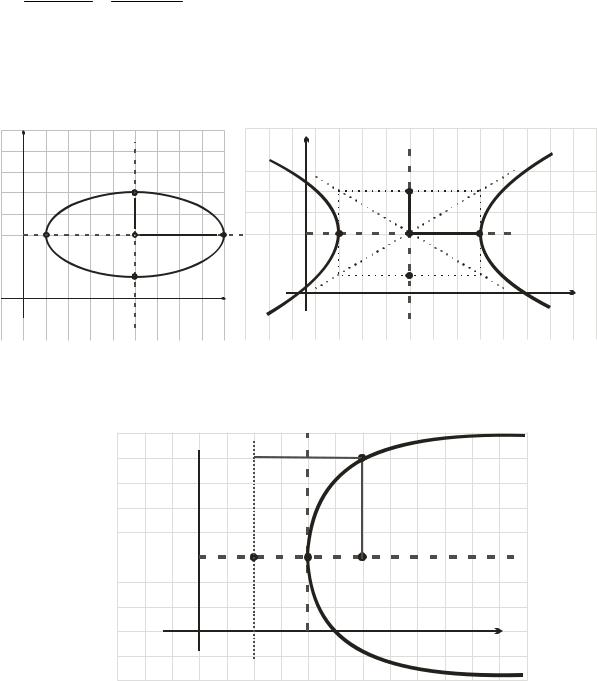
2) x xo 2 y yo 2 1, гипербола (рис. 1б); a2 b2
3) y yo 2 2p x xo , парабола (рис. 1в).
y |
y |
|
b |
a |
|
|
|
b |
y0 |
|
|
y0 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x0 |
|
x |
|
|
x0 |
|
|
|
|
|
|
а) |
|
|
|
|
б) |
y
р
р
y |
р/2 |
р/2 |
0 |
|
|
x0 x
в)
Рис. 1.
Пример. Привести уравнение кривой второго порядка
x2 4xy y2 x y 1 0
к каноническому виду. Построить чертеж.
82
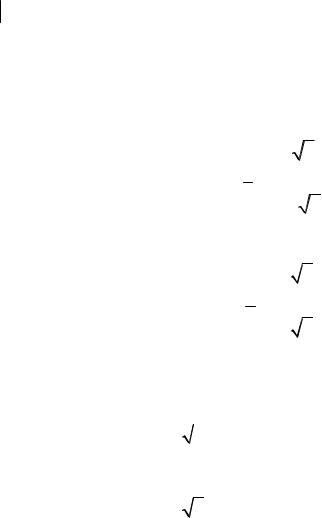
1 |
2 |
– матрица квадратичной формы, |
Решение. A |
|
|
2 |
1 |
|
B 1 |
1 T |
– линейные коэффициенты. |
Найдем ортонормированный базис из собственных векторов и приведем матрицу А к диагональному виду. Для этого вычислим собственные значения матрицы А:
A E |
|
|
1 |
2 |
2 2 3 0, |
|
|
||||||
|
2 |
1 |
||||
|
|
|
|
|
||
|
|
|
|
1 1, |
2 3. |
|
Найдем собственные векторы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
2 |
2 x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
1 |
|
|
|
x y |
|
|
|
u |
|
|
|
|
|
|
; |
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
||||||||||
|
|
|
2 |
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||
|
|
2 |
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
3 |
|
0 |
|
x y |
|
|
u |
|
|
|
|
|
. |
||||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||
|
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||
Запишем матрицы перехода: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
T |
|
|
|
2 |
|
|
, |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
ОНБ B |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
T |
|
|
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
B ОНБ |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При переходе в ортонормированный базис коэффициенты изменятся следующим образом:
1 |
0 |
|
, |
|
AОНБ |
0 |
3 |
|
|
|
|
|
||
83

|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
BTОНБ B 1 1 |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Следовательно, уравнение приобретет вид: |
|
x' 2 |
3 y' 2 |
|
|
x' 1 0, |
|
|
||||||||||||||||||||||||||||
|
2 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x' |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
TB ОНБ |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
y' |
|
|
y |
|
|
x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 y' |
2 |
|
1 |
|
||||||||
Выделим полный квадрат по первой переменной: x' |
|
|
|
|
|
|
|
|
0, |
|||||||||||||||||||||||||||
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y' |
2 |
|
|
x' |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
и получим каноническое уравнение гиперболы: |
|
|
|
|
|
|
|
|
|
1. |
|
|
||||||||||||||||||||||||
1/6 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/2 |
|
|
|
|
|
|
|
|
|||||||||
Уравнение может быть записано в альтернативных формах:
x y 2 |
x y |
|
1 |
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 (наиболее удобно для построения чертежа), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
||||||
1/6 |
1/2 |
|
|
|
||||||||||||||
3 x y 2 x y 1 2 1,

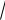 3x
3x 
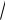 3y 2 x y 1 2 1 (нормальная форма).
3y 2 x y 1 2 1 (нормальная форма).
Построим |
|
чертеж |
кривой. Из начала координат построим единичные |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|||||||
векторы |
u |
|
|
|
|
|
и |
u |
|
|
|
и проведем новые координатные оси Оy' и |
||||||
1 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Оx' (рис.2а). Ось О'y'' |
получим параллельным переносом оси Оy' |
в «новое» |
|||||||
начало координат, |
точку О': x' |
1 |
|
, y' 0 (рис.2б); ось |
О'x'' |
визуально |
|||
|
|
|
|||||||
|
|||||||||
|
|
2 |
|
|
|
|
|
||
совпадает с осью |
Оx' . |
Отметим полуоси гиперболы (a |
|
|
по O'x'' и |
||||
1/6 |
|
||||||||
|
|
84 |
|
|
|
||||
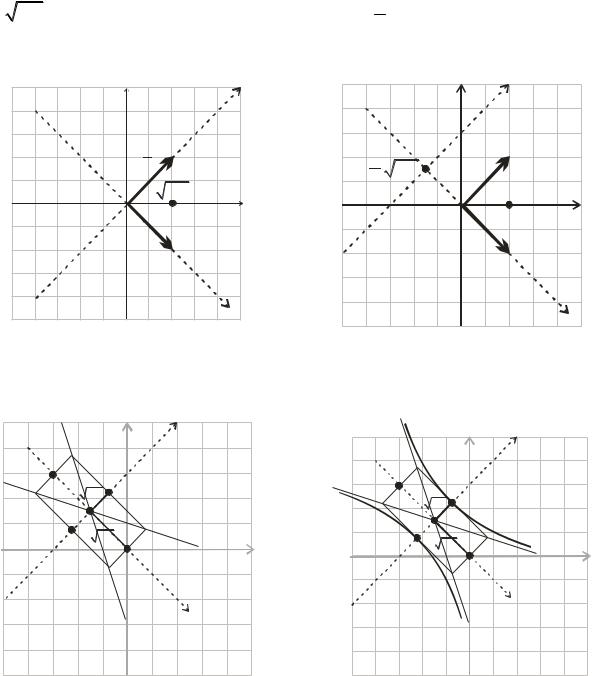
b |
1/2 |
по O'y'' ) и проведем асимптоты |
||
гиперболы (рис.2г). |
|
|
||
|
|
y |
|
y’ |
|
|
u2 |
|
|
|
|
|
1/2 |
x |
|
|
u1 |
|
|
|
|
|
|
x’ |
|
|
а) |
|
|
|
|
y |
y’’ |
|
|
|
1/6 |
|
|
|
|
1/2 |
|
x |
|
|
|
x’ |
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
Рис. 2. |
|
|
|
|
85 |
y'' b x'' |
(рис.2в). Построим ветви |
|
a |
|
|
|
|
y |
|
|
y’’ |
1/2 |
u2 |
|
|
|
x |
|
|
u1 |
|
|
x’ |
|
|
б) |
|
|
y |
|
|
y’’ |
|
|
1/6 |
|
|
1/2 |
|
|
x |
|
|
x’ |
|
|
г) |
Упражнения и задачи
Привести уравнение кривой второго порядка к каноническому виду.
15.1.5x2 6xy 5y2 1.
15.2.17x2 12xy 8y2 1.
15.3.5x2 6xy 5y2 10x 6y 4 0.
15.4.17x2 12xy 32x 8y2 16y 16 1.
15.5.3x2 10xy 8x 3y2 8y 5 0.
15.6.x2 2xy 4x y2 4y 1 0.
15.7.3x2 10xy 3y2 0.
86
16. Поверхности второго порядка
Поверхность второго порядка – это геометрическое место точек, координаты которых удовлетворяют общему уравнению
a11x2 a22y2 a33z2 a12xy a13xz a23yz a1x a2y a3z a0 0.
Уравнение можно записать в матричном виде:
|
|
|
|
|
|
|
a12 |
|
a13 |
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
2 |
|
|
|
|
x |
|
|
|
||||||||||
|
|
|
a12 |
|
|
|
x |
|
|
|
|
|
||||||||
x |
y z |
|
|
|
a |
|
a23 |
y |
|
a a |
a |
y |
|
a |
|
0. |
||||
|
|
|
|
|
|
|
0 |
|||||||||||||
|
|
2 |
|
|
|
22 |
2 |
|
|
|
1 2 |
3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
a13 |
|
|
|
a23 |
|
|
|
|
z |
|
|
|
z |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
2 |
33 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Переходя к ортонормированному базису из собственных векторов матрицы квадратичной формы, уравнение можно привести к виду
x y z |
T |
1 |
|
0 |
0 |
|
|
|
|
x |
|
|||||
|
0 |
|
|
|
0 |
T |
|
|
y |
|
|
|||||
|
|
|
|
2 |
|
|
|
B |
ОНБ |
|
|
|
||||
|
|
|
ОНБ B |
|
|
|
|
|
|
|
|
|
||||
x ' |
|
y |
' z ' |
|
0 |
|
0 3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
z |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x ' y ' |
z ' T |
|
. |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a a |
|
a |
T |
|
T |
|
|
|
y |
|
a 0 |
|
|
|||
|
|
B ОНБ |
|
|
|
0 |
|
|
|
|||||||
1 |
|
2 |
3 |
ОНБ |
B |
|
|
|
|
|
|
|
||||
|
1 |
2 |
3 |
|
|
|
|
|
z |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x ' |
y ' |
z ' T |
|
|
|
|
|
||
Выделяя полные квадраты по переменным, получим канонический вид уравнения. Типы поверхностей второго порядка сводятся к следующим:
|
|
x x |
2 |
|
|
|
|
y y |
o |
2 |
|
|
z z |
o |
2 |
||||||||||||||
1) |
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
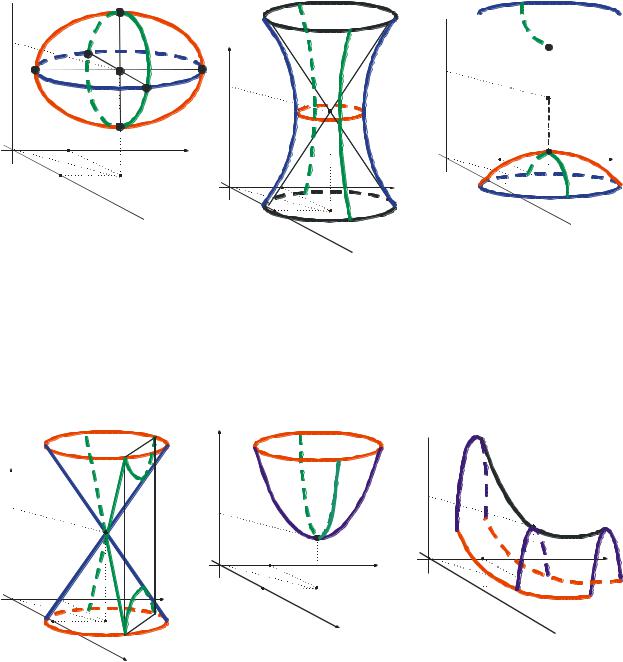
1, эллипсоид (рис. 3а); |
|||||
a |
2 |
|
|
|
b |
2 |
|
|
|
|
|
c |
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x x |
2 |
|
|
|
y y |
2 |
z z |
|
2 |
|
|
|
|
||||||||||||||
2) |
|
|
o |
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
o |
|
|
|
|
1, гиперболоид однополостный (рис. 3б); |
||||||
|
a |
2 |
|
|
|
|
2 |
|
|
|
|
c |
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x x |
2 |
|
|
|
y y |
2 |
z z |
|
2 |
||||||||||||||||||
3) |
|
|
|
o |
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
o |
|
|
|
|
1, гиперболоид двуполостный (рис. 3в); |
|||||
|
a2 |
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|||||
|
|
x x |
2 |
|
|
|
|
y y |
2 |
|
|
z z |
o |
2 |
|||||||||||||||
4) |
|
|
|
o |
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
0, конус (рис. 4а); |
||||
|
a |
2 |
|
|
|
|
b |
2 |
|
|
|
|
|
|
c |
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87 |
|||
|
x x |
2 |
y y |
2 |
||||
5) |
|
o |
|
|
o |
|
2p z zo , параболоид эллиптический (рис. 4б); |
|
a |
2 |
|
b2 |
|
||||
|
|
|
|
|
|
|||
|
x x |
2 |
y y |
2 |
||||
6) |
|
o |
|
|
|
o |
|
2p z zo , параболоид гиперболический (рис. 4в). |
a |
2 |
|
|
b2 |
|
|||
|
|
|
|
|
|
|||
 z
z
zo с z
a b |
zo |
|
yo |
y |
|
|
y |
|
xo |
yo |
|
xo |
|
|
|
|
x
x
б) Однополостный а) Эллипсоид. гиперболоид
Рис. 3.
|
|
z |
|
z |
|
|
|
zo |
|
zo |
|
с |
|
yo |
y |
|
|
|
|
y |
y |
o |
|
o |
x |
|
|
xo |
|
x |
|
|
|
|
|
x |
|
б) Эллиптический |
|
а) Конус |
|
параболоид |
|
|
|
|
|
Рис. 4.
 z
z 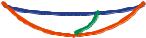 zo
zo
 с
с
yo  y
y
 x
x o
o







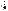

x
в) Двуполостный гиперболоид
 z
z
zo
yo
y

 xo
xo








x
в) Гиперболический параболоид
Все поверхности второго порядка, в каноническое уравнение которых входят не все переменные, называются цилиндрическими. Цилиндрические поверхности «вытянуты» вдоль отсутствующей в уравнении координатной оси
88
и полностью определяются своими направляющими – кривыми второго порядка.
Упражнения и задачи
Привести уравнение поверхности второго порядка к каноническому виду.
16.1.x2 2x 4y2 8y z2 2z 2 0.
16.2.5x2 5y2 6xy 8x 8y z2 0.
16.3.6x2 6y2 17z2 8xy 14xz 14yz 4 0.
16.4.17x2 5y2 5z2 14xy 14x 10yz 10x 2y 2z 2 0.
89
Контрольная работа 1. Циклические группы
Построить циклическую группу, порожденную данной подстановкой :
1)указать порядок группы;
2)указать обратный элемент к порождающему элементу группы;
3)вычислить 120 .
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Вариант 1. |
6 |
3 |
1 |
5 |
4 |
2 |
. |
|
|
||||||
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Вариант 2. |
6 |
1 |
3 |
5 |
4 |
2 |
. |
|
|
||||||
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Вариант 3. |
2 |
6 |
3 |
5 |
4 |
1 |
. |
|
|
||||||
1 |
2 |
3 |
4 |
5 |
6 |
|
Вариант 4. |
3 |
4 |
5 |
6 |
2 |
. |
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Вариант 5. |
6 |
5 |
4 |
3 |
2 |
1 |
. |
|
|
||||||
Вариант 6. |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
6 |
3 |
1 |
5 |
4 |
2 |
. |
|
|
|
|
||||||
Вариант 7. |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
2 |
4 |
1 |
3 |
6 |
5 |
. |
|
|
|
|
||||||
Вариант 8. |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
6 |
3 |
2 |
5 |
4 |
1 |
. |
|
|
|
|
||||||
90
