
656_Lytkina_D.V._Algebraicheskie_struktury_
.pdf
2.6. Проверить, является ли группой алгебраическая система:
а)  {0},
{0},  ;
;
б)  ,
,  ;
;
в)  ,
,  ;
;
г)  ,
,  ;
;
д)  ,
,  ;
;
е)  {0},
{0},  ;
;
ж)  {0},
{0},  ;
;
з)  ,
,  ;
;
и)  ,
,  ;
;
к)  ,
,  ;
;
л)  ,
,  ;
;
м)  \{0},
\{0},  .
.
2.7.Проверить, является ли кольцом алгебраическая система:
а)  {0}, ,
{0}, ,  ;
;
б)  , ,
, ,  ;
;
в)  , ,
, ,  ;
;
г)  {0}, ,
{0}, ,  ;
;
д)  , ,
, ,  ;
;
е)  , ,
, ,  .
.
2.8.Проверить, является ли полем алгебраическая система  M, ,
M, ,  , где M –
, где M –
следующее множество чисел:
а) M a b
 2 a,b ;
2 a,b ;
б) M a b
 2 a,b ;
2 a,b ;
в) M a b3
 2 a,b ;
2 a,b ;
г) M a b3 2 a,b ;
2 a,b ;
д) M a b3
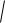 2 c3
2 c3
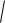 4 a,b,c ;
4 a,b,c ;
е) M a b3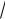 2 c3
2 c3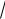 4 a,b,c .
4 a,b,c .
11

3. Циклические группы. Группа подстановок
Циклическая группа – это группа, все элементы которой являются степенями некоторого порождающего элемента:
a M : |
b M |
n |
b a a ... a an. |
|
|
|
|
|
|
|
n |
Порядком элемента циклической группы называется наименьшая степень, в которой он равен единице. В случае, если такой степени не существует, говорят, что элемент имеет бесконечный порядок. Циклическая группа, порожденная элементом a, обозначается как  a
a .
.
Порядок циклической группы равен порядку порождающего элемента. Циклическая группа может быть бесконечной, например, группа  ,
,  .
.
Порядок бесконечной циклической группы равен бесконечности. Порядок конечной циклической группы равен числу элементов носителя. Примером циклической группы является мультипликативная группа  1
1 .
.
Подстановка – это взаимно однозначное отображение непустого конечного множества на себя, т.е. :M M . Без ограничения общности можно считать, что M 1,2,...,n . Подстановку множества из n элементов
называют подстановкой степени n. Обычно, если множество M конечно, для записи подстановки используется табличная форма
|
1 |
2 |
3 |
... |
n |
, |
(k) i , |
i 1,2,...,n |
k |
|
. |
||
1,n |
|||||||||||||
|
|
i |
i |
i |
... |
i |
|
|
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
2 |
3 |
|
n |
|
|
|
|
|
|
||
Множество всех подстановок множества M обозначается как S(M). |
|||||||||||||
Если элемент отображается сам на себя (т.е. k k ), |
то он называется |
||||||||||||
неподвижным. В противном случае элемент называется действительно перемещаемым. Тождественная подстановка – это подстановка, состоящая только из неподвижных элементов, она обычно обозначается как .
Множество всех действительно перемещаемых элементов подстановки
называется |
носителем |
|
подстановки: supp( ) k |
|
k k . Очевидно, что |
|||||||||||||||||
|
|
|||||||||||||||||||||
носитель тождественной подстановки – пустое множество. |
|
|
|
|||||||||||||||||||
Произведение двух подстановок |
и |
|
|
одной и той же степени одного и |
||||||||||||||||||
того же множества определим как сложную функцию |
k |
следующим |
||||||||||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 ... |
n |
i |
i |
i |
... |
i |
|
|
1 |
2 |
3 ... |
n |
||||||||
|
i |
i |
i ... |
i |
|
|
1 |
1 |
1 |
... |
1 |
|
|
j |
j |
|
j ... |
j |
. |
|||
|
|
|
j |
j |
j |
j |
n |
|
2 |
n |
||||||||||||
1 |
2 |
3 |
n |
1 |
2 |
3 |
|
|
1 |
|
3 |
|
||||||||||
12

Нетрудно убедиться, что система  S(M),
S(M),  является группой (упр. 3.6). Для
является группой (упр. 3.6). Для
любой подстановки обратная подстановка определяется как обратное отображение:
1 |
1 |
2 |
3 |
... |
n 1 |
i |
i |
i ... |
i |
|
|
|
i2 |
i3 |
... |
|
|
1 |
2 |
3 |
n |
. |
|
|
i1 |
in |
|
1 |
2 |
3 ... |
n |
||||
Рассмотрим некоторую подстановку S(M) конечного множества M и |
|||||||||||
произвольный элемент |
k1 supp( ). |
|
Рассмотрим |
последовательность |
|||||||
элементов: k2 k1 , |
k3 |
k2 |
и т.д. |
Пусть s |
– наименьшее натуральное |
||||||
число, такое, что ks 1 ks k1 (такое число существует, так как M конечно).
Множество k1,k2,...ks называется нетривиальной орбитой подстановки
длины s. Орбита, состоящая из одного элемента, называется тривиальной. Очевидно, что этот единственный элемент является неподвижным.
Множество M относительно подстановки разбивается на объединение орбит, а supp( ) – на объединение нетривиальных орбит:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
2 |
4 |
5 |
1 |
3 |
7 |
6 |
|
|
|
|||||||
1,2,3,4,5,6,7 1,2,4 3,5 6,7 .
орбиты
В соответствие с разбиением множества supp( ) на объединение непересекающихся орбит существует удобная форма записи подстановки в виде произведения независимых циклов.
Цикл – это подстановка S(M) вида |
i |
i |
... |
i |
k |
... |
k |
|
|
, |
|
|
1 |
2 |
... |
s |
1 |
... |
k |
t |
|
||
|
|
i |
i |
i |
k |
t |
|
|
|||
|
2 |
3 |
|
1 |
1 |
|
|
|
|||
где i1,i2,...,is,k1,...,kt 1,2,...,n , называется циклом длины s. Цикл длины 2
называется транспозицией. Циклы и называются независимыми, если supp( ) supp( ) . Нетрудно убедиться, что если множество M относительно подстановки разбивается на объединение m орбит
supp( ) i11,i21,...,is11 i12,i22,...,is22 ... i1m,i2m,...,ismm ,
то подстановка представима в виде произведения m независимых циклов:
1 |
1 |
|
1 |
1 |
|
1 |
2 |
2 |
|
2 |
2 |
|
|
2 |
m m |
|
m |
m |
|
m |
|
i1 |
i2 |
... |
is1 |
k1 |
... |
kt1 |
i1 |
i2 |
... |
is2 |
k1 ... |
kt2 |
... i1 |
i2 |
... |
ism |
k1 |
... |
ktm , |
||
i1 |
i1 |
... |
i1 |
k1 |
... |
k1 |
i2 |
i2 |
... |
i2 |
k2 ... |
k2 |
im |
im |
... |
im |
km |
... |
km |
||
2 |
3 |
|
1 |
1 |
|
t1 |
2 |
3 |
|
1 |
1 |
|
|
t2 |
2 |
3 |
|
1 |
1 |
|
tm |
j |
j |
j |
j |
j |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1,m. |
|
|
|
|
|
|
|
|
||||||||
где i1 |
,i2 |
,...,isj |
,k1 |
,k2 |
,...,ktj 1,2,...,n , |
|
|
|
|
|
|
|
|
||||||||
13

Такое представление подстановки называют разложением в произведение независимых циклов и записывают в виде
i11,i21,...,i1s1 i12,i22,...,is22 ... i1m,i2m,...,ismm
или, если необходимо указать неподвижные элементы, в виде
i11,i21,...,i1s1 i12,i22,...,is22 ... i1m,i2m,...,ismm k1 ... kt ,
где k1 ,k2 ,...,kt M \ m i1j,i2j,...,isjj – неподвижные элементы .
j 1
Каждая подстановка порождает циклическую группу с операцией .
Пример 1. Определить циклическую группу, порожденную подстановкой
1 |
2 |
3 |
4 |
||
|
2 |
1 |
4 |
3 |
. |
|
|
||||
Решение. Тождественная подстановка получится как квадрат порождающего элемента, следовательно, порядок группы равен 2, обратный к порождающему элементу равен ему самому:
1 2 3 4 2 |
1 2 3 4 |
, |
|||
|
2 1 4 3 |
|
|
|
|
|
|
1 2 3 4 |
|
|
|
1 .
Получаем, что 

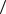 ; ,
; ,  . Никаких других элементов мы не получим,
. Никаких других элементов мы не получим,
например, при возведении порождающего элемента в третью степень имеем
1 2 3 4 3 |
1 2 3 4 |
. |
█ |
||||
|
2 1 4 3 |
|
|
2 1 4 3 |
|
||
|
|
|
|
|
|
||
|
|
Пример |
2. Записать |
|
элементы |
|
группы подстановок S 3 , , |
|||||||
3 1;2;3 . |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
Решение. Элементами группы являются подстановки вида i |
i |
i |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
1 |
|
2 |
3 |
|
|
1 |
2 |
3 |
1 1, |
|
|
|
|
|
|
2 |
, |
|
1 |
1 |
3 |
|
|
|
|
|||
|
1 |
|
3 |
|
|
2 |
|
|
|
|
|
|||
|
1 |
2 |
3 |
2 1, |
|
1 |
2 |
3 |
3 1, |
|
|
|
||
2 |
3 |
2 |
|
3 |
3 |
2 |
|
|
|
|
||||
|
|
1 |
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
1 |
2 |
3 |
|
5 1, |
|
1 |
2 |
3 |
|
4 1. |
||
4 |
2 |
3 |
1 |
|
5 |
3 |
1 |
2 |
|
||||
|
|
|
|
|
|
|
|
||||||
Запишем результат применения к элементам группы операции в виде таблицы умножения (таблицы Кэли):
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
1 |
1 |
|
4 |
5 |
2 |
3 |
|
|
|
|
|
|
|
2 |
2 |
5 |
|
4 |
3 |
1 |
|
|
|
|
|
|
|
3 |
3 |
4 |
5 |
|
1 |
2 |
|
|
|
|
|
|
|
4 |
4 |
3 |
1 |
2 |
5 |
|
|
|
|
|
|
|
|
5 |
5 |
2 |
3 |
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
█ |
Пример 3. Разложить подстановку |
|
|
в произведение независимых |
||||
циклов |
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
2 |
5 |
6 |
4 |
1 |
3 |
. |
|
|
||||||
Решение. Найдем орбиты подстановки и соответствующие им
независимые циклы: |
|
|
|
|
|
|
|
|
(1) 2, (2) 5, (5) 1, 1,2,5 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
– орбита, |
2 |
5 |
3 |
4 |
1 |
6 |
; |
|
|
|
|
||||||
(3) 6 |
1 |
2 |
3 |
4 |
5 |
6 |
|
, (6) 3, 3,6 – орбита, |
2 |
6 |
4 |
5 |
3 |
; |
|
|
1 |
|
|||||
|
(4) 4 – неподвижный элемент. |
|
|
|
|
|
|
Следовательно, (1,2,5)(3,6) (1,2,5)(3,6)(4). |
|
|
|
█ |
|||
15

Упражнения и задачи
3.1. Доказать, что для любого элемента циклической группы верно
am *an am n, |
am n am n , m,n . |
3.2.Доказать, что предыдущее утверждение имеет место для любого элемента произвольной группы.
3.3.Доказать, что подгруппа циклической группы также является циклической.
3.4.Доказать, что порядок подгруппы конечной циклической группы является делителем порядка группы.
3.5.Доказать, что любая подгруппа аддитивной группы целых чисел имеет вид
 n ,
n ,  , n , где n 0, n, 2n, 3n,... .
, n , где n 0, n, 2n, 3n,... .
3.6.Доказать, что если a,b,c– элементы некоторой группы, то
а) ab и ba имеют одинаковый порядок;
б) aba 1 и b имеют одинаковый порядок;
в) abc,bca,cab имеют одинаковый порядок.
3.7.Доказать, что  S(M),
S(M),  – группа.
– группа.
3.8.Доказать, что каждая нетождественная подстановка разлагается в произведение транспозиций.
3.9.Доказать, что S(M) M !.
3.10.Записать следующие подстановки в виде произведения независимых циклов:
а) |
1 |
2 |
3 |
4 |
5 |
; |
|
|
|
|
||
|
4 |
1 |
5 |
2 |
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
б) |
1 |
2 |
3 |
4 |
5 |
|
6 |
; |
|
|
||
|
6 |
5 |
1 |
4 |
2 |
|
3 |
|
|
|
||
|
|
|
|
|
|
|
||||||
в) |
1 |
2 |
3 |
4 |
5 |
|
6 |
|
7 |
8 |
|
|
|
8 |
1 |
3 |
6 |
5 |
|
7 |
|
4 |
2 |
. |
|
|
|
|
|
|
||||||||
3.11.Записать следующие подстановки в виде произведения независимых циклов:
а) |
1 |
2 |
3 |
4 ... |
2n 1 |
2n |
; |
|
|
2 |
1 |
4 |
3 ... |
2n |
|
||
|
|
2n 1 |
|
|||||
|
|
|
|
|
|
|
16 |
|
б) |
1 |
2 |
3 |
4 |
5 |
6 ... |
3n 2 |
3n 1 |
3n |
|
|
|
3 |
2 |
1 |
6 |
5 |
4 ... |
3n |
3n 1 |
3n 2 |
. |
|
|
|
|
|||||||||
3.12.В следующих подстановках перейти от записи в виде произведения независимых циклов к записи таблицей:
а) (1,5)(2,3,4);
б) (1,3)(2,5)(4);
в) (1,2)(3,4)...(2n 1,2n).
3.13.Вычислить:
а) |
1 |
2 3 4 5 |
1 2 3 |
4 5 |
|
|
||||||||||
|
4 |
1 5 2 3 |
|
|
|
|
|
5 4 |
; |
|
|
|||||
|
|
|
1 3 2 |
|
|
|
||||||||||
б) |
1 |
2 3 4 5 6 |
1 2 |
3 4 5 6 |
; |
|||||||||||
|
6 |
|
|
|
|
|
|
|
5 6 |
2 3 4 1 |
|
|||||
|
|
5 1 4 2 3 |
|
|
|
|||||||||||
в) |
1 |
2 3 |
4 5 6 7 8 2 |
; |
|
|
|
|
||||||||
|
8 |
1 |
3 |
6 |
5 |
|
7 |
4 |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
г) |
1 |
2 |
3 |
4 |
5 3 |
|
|
|
|
|
|
|
|
|||
|
4 |
1 |
5 |
2 |
3 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
д) |
1 |
2 |
3 |
4 |
5 20 |
|
|
|
|
|
|
|
|
|||
|
4 |
1 |
5 |
2 |
3 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
е) |
1 |
2 |
3 |
4 |
5 |
|
6 |
7 |
8 |
|
9 |
10 150 |
|
|
||
|
3 |
5 |
4 |
6 |
9 |
|
7 |
1 |
10 |
8 |
2 |
. |
|
|
||
|
|
|
|
|
|
|||||||||||
3.14. Найти подстановку, обратную данной:
а) |
1 |
2 |
3 |
4 |
5 |
|
; |
|
|
4 |
1 |
5 |
2 |
3 |
|
||
|
|
|
|
|||||
1 |
2 |
3 |
4 |
5 |
6 |
|
; |
|
б) |
5 |
6 |
2 |
3 |
4 |
1 |
|
|
|
|
|
||||||
в) (1,5)(2,3,4);
17
г) (1,3)(2,5)(4).
3.15.Решить уравнения:
а) A X B C ,
б) A2 X C B,
в) X B30 C,
1 2 3
если A 7 3 2
1 |
2 |
3 |
|
B |
3 |
1 |
2 |
|
|||
1 |
2 |
3 |
|
C |
5 |
1 |
3 |
|
|||
4 |
5 |
6 |
7 |
|
|
|
1 |
6 |
5 |
4 |
, |
||
|
|
|||||
4 |
5 |
6 |
7 |
|
, |
|
7 |
4 |
5 |
6 |
|
||
|
|
|||||
4 |
5 |
6 |
7 |
|
|
|
6 |
4 |
7 |
2 |
. |
||
|
|
|||||
18

4. Кольца вычетов. Поля Галуа. Кольцо квадратных матриц
Говорят, что числа a и b равны по модулю n (n ), если они имеют одинаковый остаток от деления на n. При этом используется запись a bmodn.
Кольцом вычетов (по модулю n) называется кольцо 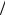 n, ,
n, ,  ,
,
n {0,1,2,...,(n 1)}, с операциями сложения и умножения по модулю n,
определяемыми следующим образом:
a b: a b modn n;
a b: a b modn n.
Поле Галуа (GF) – это любое конечное поле. В частности, конечным полем, а следовательно, и полем Галуа является кольцо 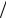 p, ,
p, , 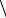 где p –
где p –
простое число (упр. 4.2).
Если |
n |
, , |
является полем Галуа, то n pk, |
k , p простое. Важно |
|
|
|
|
отметить, что операции в поле Галуа в общем случае не обязательно являются сложением и умножением по модулю n.
Пример 1. Задать операции сложения и умножения в поле F4  4, ,
4, ,  .
.
Решение. Определим в первую очередь операцию умножения. Умножение в F4  4, ,
4, ,  невозможно определить как умножение по модулю
невозможно определить как умножение по модулю
4, так как в этом случае, |
2 2 4 0mod4, т.е. 2 является делителем нуля, чего |
в поле быть не может. |
Итак, поскольку произведение числа на нуль в поле |
должно быть равно нулю, имеем: |
0 k k 0 0, |
k 0;3. |
Далее, по |
|||||||
определению единицы, имеем: 1 k k 1 k, k |
|
. |
Осталось |
определить |
||||||
0;3 |
||||||||||
2 2, |
2 3 3 2 и 3 3. Заметим, что |
для любого k |
|
все произведения |
||||||
1;3 |
||||||||||
k m, |
m |
|
должны быть различны, |
так как: k m1 k m2 |
влечет m1 m2 |
|||||
0;3 |
||||||||||
(см. упр. 2.4).
Рассмотрим поочередно все оставшиеся варианты. Допустим, 2 2 1, тогда 2 3 3, т.е. 2=1 – противоречие. Остается вариант 2 3 1, 2 2 3, и, следовательно, 3 3 2. Запишем таблицу Кэли:
|
0 |
1 |
2 |
3 |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
3 |
2 |
0 |
2 |
3 |
1 |
3 |
0 |
3 |
1 |
2 |
|
|
19 |
|
|

Определить операцию сложения как сложение по модулю 4 тоже не получится, так как в этом случае умножение относительно сложения не будет обладать свойством дистрибутивности (проверить самостоятельно). Итак, приступим к последовательному заполнению таблицы Кэли для сложения в F4  4, ,
4, ,  .
.
Так как a 0 0 a a (по определению нуля), то имеем
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
|
0 |
0 |
1 |
2 |
3 |
|
1 |
1 . . . |
. |
|||
2 |
2 . . . |
|
|||
3 |
3 . . . |
|
|||
Сумма 1 2 не может быть равна 2 (или 1), так как это означает, что 1 (или 2) – нейтральный элемент по сложению (нуль). Предположим, 1 2 0 (т.е. 2 – противоположный к 1). Тогда
3 (1 2) 3 0 0.
С другой стороны,
3 (1 2) 3 1 3 2 3 1.
Следовательно, 3+1=0, значит, 3 также является противоположным элементом к 1. Получаем противоречие, так как противоположный элемент должен быть только один. Остается единственный вариант:1 2 3. Рассуждая аналогичным образом, получим, что 1 3 0, 1 3 1, 1 3 3 и 2 3 0, 2 3 2, 2 3 3. Следовательно, 1 3 2 и 2 3 1.
С учетом коммутативности операции, таблица Кэли принимает вид
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
|
0 |
0 |
1 |
2 |
3 |
|
1 |
1 . |
3 |
2 |
. |
|
2 |
2 |
3 |
. |
1 |
|
3 |
3 |
2 |
1 . |
|
|
У каждого элемента поля должен быть противоположный элемент, следовательно, недостающие элементы таблицы – нули.
|
|
|
0 |
1 |
2 |
3 |
|
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
2 |
3 |
|
0 |
0 |
0 |
0 |
0 |
|
|
|
Итак, F4 |
4, , : |
1 |
1 |
0 |
3 |
2 |
, |
|
1 |
0 |
1 |
2 |
3 |
. |
█ |
|
|
2 |
2 |
3 |
0 |
1 |
|
|
2 |
0 |
2 |
3 |
1 |
|
|
|
|
3 |
3 |
2 |
1 |
0 |
|
|
3 |
0 |
3 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
