Пример 1

Найти эмпирическую функцию по закону распределению выборки

x	1	4	6
n	10	15	25

Решение. Найдем объем выборки: n=10+15+25=50.

Наименьшая варианта равна 1, поэтому F*(x)=0 при x 1. Значение X<4, а именно: x и x наблюдались 10+15=25 раз. Следовательно, F*(x)= при 4<x 6. Т.к. x=6-наибольшая варианта, то F*(x)=1 при x>6. Напишем искомую эмпирическую функцию:

0 при x

F*(x)= 0,2 при 1<x

0,5 при 4<x

1 при x>6.

F(x)

Рисунок 1 –График функции

Полигон и гистограмма

A) Дискретное распределение признака X. Полигоном частот называют ломаную, отрезки которой соединяют точки (x ,…(x где x -варианты выборки и n -соответствующие им частоты.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x ,…,(x где x -варианты выборки и W -соответствующие им относительные частоты.

B) Непрерывное распределение признака X. При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины K и находят n -сумму частот вариант, попавших в i-й интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению h /h(плотность частоты). Площадь частичного i-го прямоугольника равна h* -частоте вариант, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению W /h (плотность относительной частоты). Площадь частичного i-го прямоугольника равна h* -относительной частоте вариант, попавших в i-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. 1.

Пример 1

Построить полигон частот по данному распределению выборки:

x	1	4	5	7
n	20	10	14	6

Решение: Отложим на оси абсцисс варианта x , а на оси ординат - соответствующие им частоты n ; соединив точки (x ) отрезками прямых, получим искомый полигон частот.

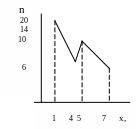
Рисунок 2 -Графики функции

Задание 1. Найти эмпирическую функцию по данному распределению выборки:

a)

x	2	5	7	8
n	1	3	2	4

b)

x	4	7	8
n	5	2	3

Задание 2. Построить полигон частот по данному распределению выборки:

a)	x	2	3	5	6	b)	x	15	20	25	30	35
	n	10	15	5	20		n	10	15	30	20	25

Задание 3. Построить полигон относительных частот по данному распределению выборки:

a)	x	2	4	5	7	10	b)	x	1	4	5	8	9
	W	0,15	0,2	0,1	0,1	0,45		W	0,15	0,25	0,3	0,2	0,1

c)	x	20	40	65	80
	W	0,1	0,2	0,3	0,4

Контрольные вопросы

1. Дать определение статистическому распределению выборки.

2. Дать определение эмпирическому функции распределения.

3. Какими свойствами обладает эмпирическая функция

4.Дать определение полигону частот

Практическое занятие 4 Статистические оценки параметров распределения

Точечные оценки

Статистической оценкой Ө* неизвестного параметра Ө*теоретического распределения называют функцию f(x от наблюдаемых случайных величин x .

Точечной называют статистическую оценку, которая определяется одним числом Ө*=f(x , где x - результаты n наблюдений над количественным признаком X(выборки).

Несмещенной называют точечную оценку, мат. ожидание которой равно оцениваемому параметру при любом объеме выборки.

Смещенной называют точечную оценку, мат. ожидание которой не равно оцениваемому параметру.

Несмещенной оценкой генеральной средней (мат. ожидания) служит выборочная средняя , где x -вариант выборки, n - частота варианта, x n= -объем выборки.

Замечание 1: Если первоначальные варианты x - большие числа, то для упрощения расчета целесообразно вычесть из каждой варианты одно и то же число C, т. е. перейти к условным вариантам U (в качестве C выгодно принять число, близкое к выборочной средней; т.к. выборочная средняя неизвестна, число C выбирают ’’на глаз’’ ). Тогда

Смещенной оценкой генеральной дисперсии служит выборочная дисперсия D эта оценка является смещенной, т.к. M[D . Более удобна формула

D

Оценка называется состоятельной, если с ростом объема выборки она дает все более точные значения характеристики случайной величины.

Замечание 2: Если первоначальные варианты x -большие числа, то целесообразно вычесть из всех вариант одно и то же число C, равное выборочной средней или близкое к ней, т.е. перейти к условным вариантам U (дисперсия при этом не изменится). Тогда D

Замечание 3: Если первоначальные варианты являются десятичными дробями с k десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число C=10 , т.е. переходят к условным вариантам U

При этом дисперсия увеличится в C раз. Поэтому, найдя дисперсию условных вариант, надо разделить ее на C : D

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия: S

Более удобна формула S

В условных вариантах она имеет вид S , причем если U то S ; если U то S

Замечание 4: При большом числе данных используют метод сумм.