
- •Основы эконометрики
- •Введение
- •(2,0; 0,0); (2,5; 0,5); (3,0; 1,0); (4,0; 1,0); (4,5; 0,5) И (5,0; 0,0), которая характеризует особый случай представления данных.
- •Задание 3.6. Рассмотрим линейную однофакторную регрессионную модель, в которой экзогенные переменные принимают только два значения 0 и 1, т.Е. Являются индикаторами.
- •Практическое занятие 5. Множественный регрессионный анализ Модель множественной линейной регрессии
- •Список литературы
- •Содержание
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Казахский национальный технический университет имени К.И..Сатпаева
Кафедра «Экономическая кибернетика»
Р.М.Алимжанова, К.К.Казбекова, Р.Т.Исмаилова
Основы эконометрики
Методические указания к практическому занятию и
по самостоятельной работе студентов по эконометрике
(для всех экономических специальностей)
Алматы 2010
УДК (075.8) 330.115
СОСТАВИТЕЛИ: Р.М.Алимжанова, К.К.Казбекова, Р.Т.Исмаилова «Основы эконометрики». Методические указания к практическому занятию и по самостоятельной работе студентов по эконометрике (для всех экономических специальностей)
Алматы: КазНТУ, 2010, с.33____.
Методические указания к практическим занятиям и по самостоятельной работе студентов по курсу «Эконометрика» содержит статистические методы анализа данных, парный регрессионный анализ и множественную регрессию. Каждый раздел включает в себе краткий теоретический курс и примеры с решениями задачи, а также задания к самостоятельной работе студентов с контрольными вопросами для закрепления тем.
Методические указания рекомендуется для студентов экономических специальностей дневного и заочного отделения, а также для самостоятельного ознакомления с этой дисциплиной
Ил.-2.Список лит. – 6 назв.
Рецензент: Лисенков А.А. д-р техн.наук.
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2009г.

КазНТУ имени К.И.Сатпаева,, 2010г
Введение
Эконометрика (экономико-статистическое моделирование) является одним из направлений экономико-математических и статистических методов анализа, которое заключается в статистическом измерении параметров математических выражений, характеризующих некоторую экономическую концепцию о взаимосвязи и развитии объекта, явления и в применении полученных таким путем экономических моделей для конкретных экономических выводов.
Цель дисциплины - овладение студентами принципами правильной формулировки экономических задач и проблем построение уравнение зависимостей применяемых в практической и управленческой деятельности.
Задачи преподавания настоящей дисциплины состоят в том, чтобы развивать у студентов экономико-математическое мышление, обучить их разрабатывать концептуальные модели и приемам их математической формализации возникающих на практике экономико-статистических и управленческих задач.
Практическое задание 1. Элементы теории вероятности и математической статистики
Математическое ожидание дискретной случайной величины. Теоретическая дисперсия дискретной случайной величины.
Математическое
ожидание дискретной случайной величины
– это взвешенное среднее всех ее
возможных значений на вероятность
соответствующего исхода. Математически
если случайную величину обозначить как
х
, то ее математическое ожидание будет
обозначаться как
![]() .
.
Предположим, что
х
может принимать n
конкретных значений (![]() )
и что вероятность получения
)
и что вероятность получения
![]() равна
равна
![]() .
Тогда математическое ожидание дискретной
случайной величины равна
.
Тогда математическое ожидание дискретной
случайной величины равна
![]() .
(1.1)
.
(1.1)
и
непрерывной случайной величины:
![]() .
.
Свойства 1. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е.
![]() . (1.2)
. (1.2)
Свойства 2. Если случайная переменная умножается на константу, то ее математическое ожидание умножается на ту же константу. Если х – случайная переменная и а – константа, то
![]() .
(1.3)
.
(1.3)
Свойства 3.
Математическое ожидание константы есть
сама эта величина, т.е.
![]()
Дисперсией
(теоретической) случайной величины х
называется математическое ожидание
квадрата отклонения х
от математического ожидания
![]() ,
т.е.
,
т.е.
![]() ,
(1.4)
,
(1.4)
следовательно, для дискретной случайной величины
![]() ,
,
а для непрерывной случайной величины
![]() .
.
Пример 1.1
Найти дисперсию случайной величины X, которая задана следующим законом распределения:
-
X
1
2
5
P
0,3
0,5
0,2
/через отклонение/
Решение: Найдем математическое ожидание:
Е(х)=1*0,3+2*0,5+5*0,2=2,3.
Найдем все возможные значения квадрата отклонения:
[x![]()
[x![]()
[x![]()
Напишем закон распределения квадрата отклонения:
-
[х-Е(х)]
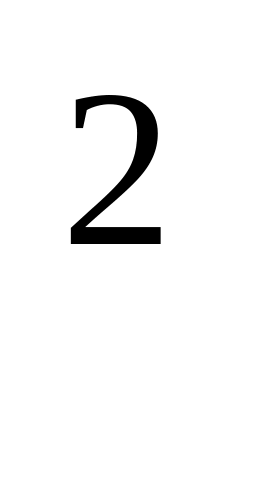
1,69
0,09
7,29
P
0,3
0,5
0,2
По
определению,
![]() =1,69*0,3+0,09*0,5+7,29*0,2=2,01.
=1,69*0,3+0,09*0,5+7,29*0,2=2,01.
Задание 1.1. Случайная переменная х определяется как разность между большим и меньшим числами, выпавшими при бросании двух костей. Если они равны между собой, то переменная х считается равной нулю. Найдите распределение вероятностей для х. Найти математическое ожидание случайной величины х. Рассчитайте Е(х2) для величины х.
Задание 1.2. Пусть х – случайная переменная с математическим ожиданием μ, и λ-константа. Докажите, что математическое ожидание λх равно λμ.
Задание 1.3. Пусть х – число очков, выпавшее при однократном бросании игральной кости. Рассчитайте возможные значения у, где у получается по формуле у=х2+3х-2 и, далее, рассчитайте Е(у). Покажите, что она равняется Е(х2)+3Е(х)-2.
Задание 1.4. Рассчитайте теоретическую дисперсию и стандартное отклонение величины х, определенной как в задание 1.
Задание 1.5.Рассчитайте дисперсию обобщенной оценки теоретического среднего для частного случая σ2=1 и выборки из двух наблюдений, с величинами λ1 от 0 до 1 при шаге 0,1. Нанесите полученные точки на график. Важно ли то, чтобы весовые коэффициенты λ1 и λ2 в точности равнялись друг другу?
Контрольные вопросы
1. Дать определение случайной переменной
2. Перечислите свойства математического ожидания.
3. Дать определение дисперсии.
Практическое занятие 2. Ковариация, дисперсия и корреляция
Выборочная ковариация является мерой взаимосвязи между двумя переменными.
При наличии n наблюдений двух переменных (х и у) выборочная ковариация между х и у задается формулой:
![]() .
.
Правила расчета ковариации.
Если
 ,
то
,
то
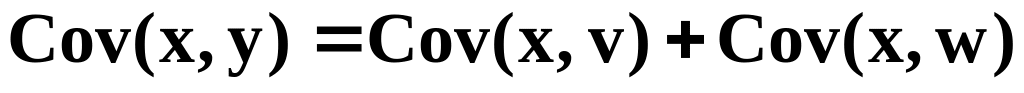 .
.Если
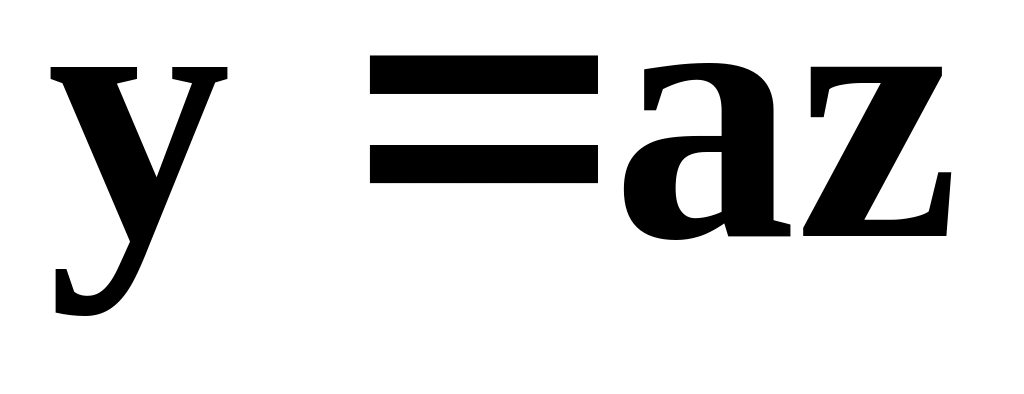 ,
где а
– константа, то
,
где а
– константа, то
 .
.Если
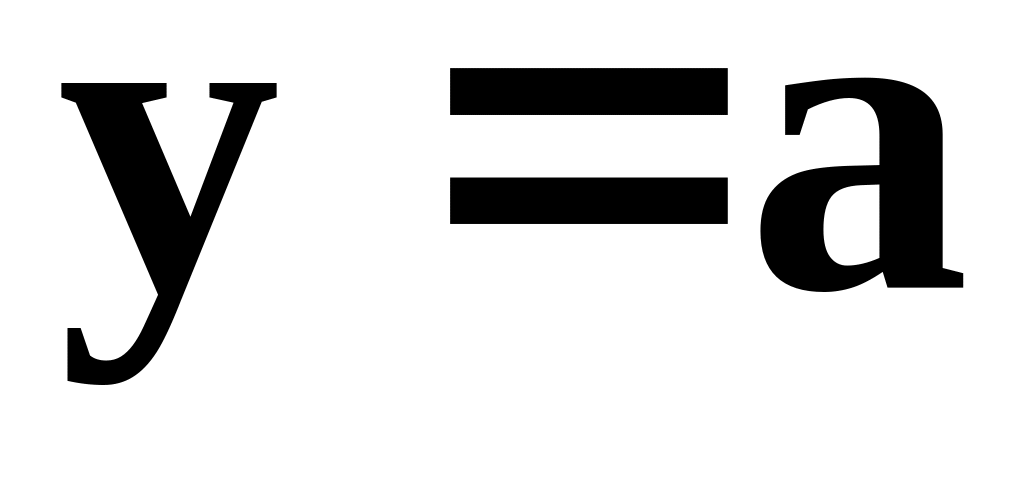 ,
где а
– константа, то
,
где а
– константа, то
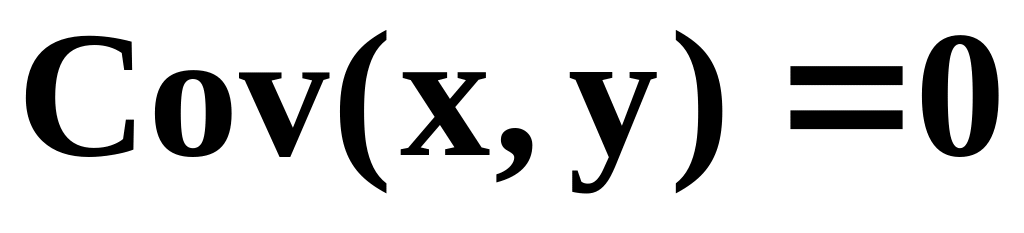 .
.
Если х
и у
– случайные величины, то теоретическая
ковариация
![]() определяется как математическое ожидание
произведения отклонений этих величин
от их средних значений:
определяется как математическое ожидание
произведения отклонений этих величин
от их средних значений:
![]()
где
![]() и
и
![]() -
теоретические средние значения х и у
соответственно.
-
теоретические средние значения х и у
соответственно.
Для выборки из n
наблюдений
![]() выборочная
дисперсия
определяется как среднеквадратичное
отклонение в выборке:
выборочная
дисперсия
определяется как среднеквадратичное
отклонение в выборке:
![]() .
.
Правила расчета дисперсии
1.Если
![]() ,
то
,
то
![]() .
.
2. Если
![]() ,
где а
является постоянной, то
,
где а
является постоянной, то
![]() .
.
Если , где а является постоянной, то
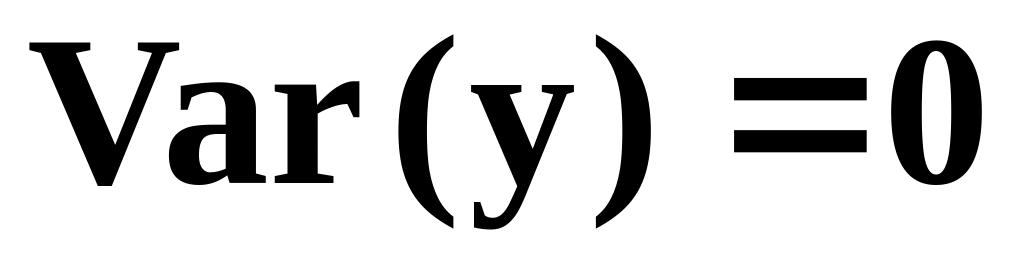 .
.Если
 ,
где а
является постоянной, то
,
где а
является постоянной, то
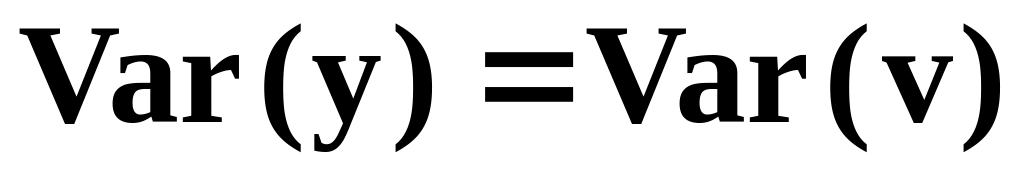 .
.
Более точной мерой зависимости является коэффициент корреляции. Коэффициент корреляции имеет две формы – теоретическую и выборочную. Теоретический коэффициент корреляции определяется следующим образом:
![]()
Выборочный коэффициент корреляции r определяется путем замены теоретических дисперсий и ковариации на их несмещенные оценки.
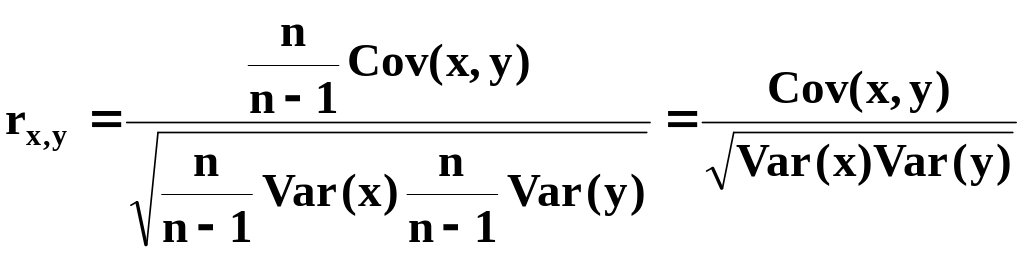 .
.
Выборочный коэффициент корреляции имеет максимальное значение, равное единице, которое получается при строгой линейной положительной зависимости между выборочными значениями х и у. Аналогичным образом r принимает минимальное значение –1, когда существует отрицательная линейная зависимость. Величина r =0 показывает, что зависимость между наблюдениями х и у в выборке отсутствует.
Пример 2.1. Пусть имеем данные по 6-ти семьям (домохозяйствам), приведенные в таблице, где x- общий годовой доход; y- расходы на питание и одежду; v-расходы на питание; w-расходы на одежду. Здесь y=v+w. Указанную в таблице 2.1величину z рассматривать пока не будем.
Покажем, что если y=v+w, то
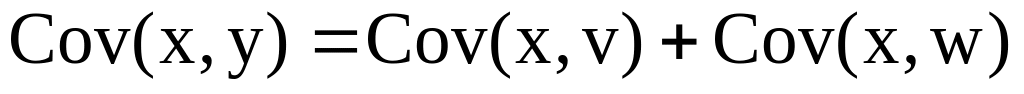
Таблица 2.1
семья |
Доход семьи х |
Расходы на питание и одежду у |
Расходы на питание v |
Расходы на одежды w |
Вторая выборка: расходы семьи на питание и одежду z |
1 |
3000 |
1100 |
850 |
250 |
2200 |
2 |
2500 |
850 |
700 |
150 |
1700 |
3 |
4000 |
1200 |
950 |
250 |
2400 |
4 |
6000 |
1600 |
1150 |
450 |
3200 |
5 |
3300 |
1000 |
800 |
200 |
2000 |
6 |
4500 |
1300 |
950 |
350 |
2600 |
Сумма |
23300 |
7050 |
5400 |
1650 |
14100 |
среднее |
3883 |
1175 |
900 |
275 |
2350 |
Для
каждой семьи вычислим величины
![]() ,
,![]() ,
,![]() ,
,![]() .
Эти данные оформим в виде таблицы 2.2.
.
Эти данные оформим в виде таблицы 2.2.
![]() ;
;
![]() ;
;![]() .
.
Таблицы
2.2![]()
Семья |
|
|
|
|
|
|
|
1 |
-883 |
-75 |
66250 |
-50 |
44167 |
-25 |
22083 |
2 |
-1383 |
-325 |
449583 |
-200 |
276667 |
-125 |
172917 |
3 |
117 |
25 |
2917 |
50 |
5833 |
-25 |
-2917 |
4 |
2117 |
425 |
899583 |
250 |
529167 |
175 |
370416 |
5 |
-583 |
-175 |
102083 |
-100 |
58333 |
-75 |
43750 |
6 |
617 |
125 |
77083 |
50 |
30833 |
75 |
46250 |
Сумма |
1597500 |
|
945000 |
|
652500 |
||
Среднее |
266250 |
|
157500 |
|
108750 |
||
Итак,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
если у=v+w,, т.е вклад семьи в
,
если у=v+w,, т.е вклад семьи в
![]() является суммой ее вкладов в
является суммой ее вкладов в
![]() ,
,
![]()
б)
Добавим последнюю колонку z, которая
определяет расходы на питание и одежду
для второй выборки из 6 семей. Предполагается,
что значения x для второго набора семей
такие же как и в первом наборе. Покажем,
что если y=az, то
![]()
Таблицы 2.3
семья |
Доход семьи х |
Расходы на питание и одежду z |
|
|
|
1 |
3000 |
2200 |
-883 |
-150 |
132500 |
2 |
2500 |
1700 |
-1383 |
-650 |
899167 |
3 |
4000 |
2400 |
117 |
50 |
5833 |
4 |
6000 |
3200 |
2117 |
850 |
1700167 |
5 |
3300 |
2000 |
-583 |
-350 |
204167 |
6 |
4500 |
2600 |
617 |
250 |
154167 |
Сумма |
23300 |
14100 |
5400 |
|
3195000 |
среднее |
3883 |
2350 |
900 |
|
532500 |
![]() ,
так как y=2z. Рассмотрим первую часть:
z=2y1
,
так как y=2z. Рассмотрим первую часть:
z=2y1
![]() .
.
![]() ,
т.е. вклад первой семьи в величину
,
т.е. вклад первой семьи в величину
![]() в точности равен двойной величине ее
вкладов
,
то же справедливо для других семей.
в точности равен двойной величине ее
вкладов
,
то же справедливо для других семей.
в) Докажем на примере правило 3 , если у=a, где а-const, то Cov(x,y)=0.
Допустим, что каждая семья имеет по 2 взрослых человека. Вычислим ковариацию между х- общим доходом и а- числом взрослых в семье.
![]() следовательно,
следовательно,
![]() и
и
![]() .
Следовательно, для каждой семьи
и
.
Следовательно, для каждой семьи
и
![]() ,
поэтому
,
поэтому
![]() .
Данные вычислений можно оформить в виде
таблицы
.
Данные вычислений можно оформить в виде
таблицы
Таблицы 2.4
-
Семья
Доход семьи
х
a
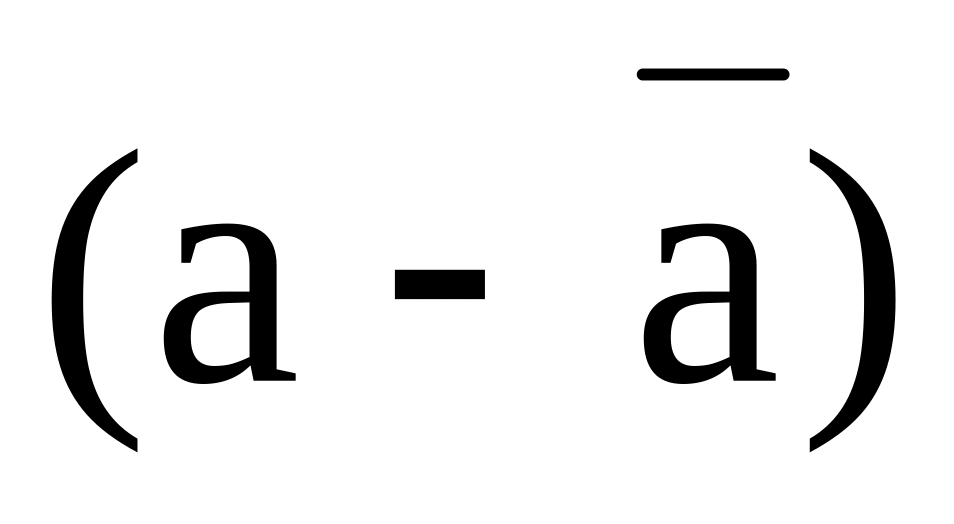
1
3000
2
-883
0
0
2
2500
2
-1383
0
0
3
4000
2
117
0
0
4
6000
2
2117
0
0
5
3300
2
-583
0
0
6
4500
2
617
0
0
Сумма
23300
12
5400
0
среднее
3883
2
900
0
Задание 2.1. В некоторой бюрократической стране годовой доход каждого индивида у определяется по формуле: у=10000+500s+200t, где s –число лет обучения индивида; t –трудовой стаж (в годах); х- возраст индивида.(таблица 2.5). Рассчитайте Cov(x,y), Cov(x,s) и Cov(x,t) для выборки из пяти индивидов, описанной ниже, и проверьте, что Cov(x,y)=500Cov(x,s)+200Cov(x,t). Объясните аналитически, почему так происходит.
Таблица 2.5
-
индивид
Возраст(годы), х
Годы обучения, s
Трудовой стаж,t
Доход, у
1
18
11
1
15700
2
29
14
6
18200
3
33
12
8
17600
4
35
16
10
20000
5
45
12
5
17000
Задание 2.2. Используя данные из задания 3, вычислите Var(y), Var(s) Var(t) и проверьте, что Var(y)=250000Var(s)+40000Var(t)+200000Cov(s,t), при этом результат объясните аналитически.
Задание 2.3. Пусть наблюдения двух случайных переменных х и у находятся на прямой линии: у=а+bx. Покажите, что Cov(x,y)=bVar(x) и что Var(y)=b2Var(x), а следовательно, выборочный коэффициент корреляции равен 1, если наклон линии положителен, и -1, если этот наклон отрицателен.
Задание 2.4.Пусть переменная у определяется строгой линейной зависимостью: у=а+bх, и предположим, что для х, у и третьей переменной z получена выборка наблюдений. Покажите, что если коэффициент b положителен, то выборочный коэффициент корреляции для у и z должен таким же, как и для х и z.
Контрольные вопросы
1.Какая оценка называется несмещенной, состоятельной и эффективной?
2.Что такое выборочная, теоретическая ковариация?
3.Что такое выборочная дисперсия?
4.Какие две формы имеет коэффициент корреляции?
Практическое занятие 3. Модель парной линейной регрессии
Регрессия по методу наименьших квадратов с одной независимой переменной.
Рассмотрим случай,
когда имеется n
наблюдений двух переменных х
и у.
Предположив, что у
зависит от х,
мы хотим подобрать уравнение
![]() .Мы
хотим выбрать а
и b,
чтобы минимизировать величину S:
.Мы
хотим выбрать а
и b,
чтобы минимизировать величину S:
![]()
Необходимые условия минимума S заключается в равенстве нулю частных производственных по а и b:
![]() ,
,
![]()
Решение этой системы двух уравнений с двумя неизвестными дают формулы:
![]() ,
,
![]() .
.
В
парном регрессионном анализе поведение
зависимой переменной объясняется
поведением независимой переменной.
Согласно определению остатков можно
записать
![]() ,
,
![]() .
.
Оказывается
справедливо следующее равенство
![]() .
.
Это означает, что
мы можем разложить Var(y)
на две части:
![]() -
часть, которая «объясняется» уравнением
регрессии и Var(e)
– «необъясненную»
часть.
-
часть, которая «объясняется» уравнением
регрессии и Var(e)
– «необъясненную»
часть.
Отношение
 - это часть дисперсии у, объясненная
уравнением регрессии. Это отношение
известно как коэффициент детерминации,
и его обычно обозначают
- это часть дисперсии у, объясненная
уравнением регрессии. Это отношение
известно как коэффициент детерминации,
и его обычно обозначают
![]() :
:
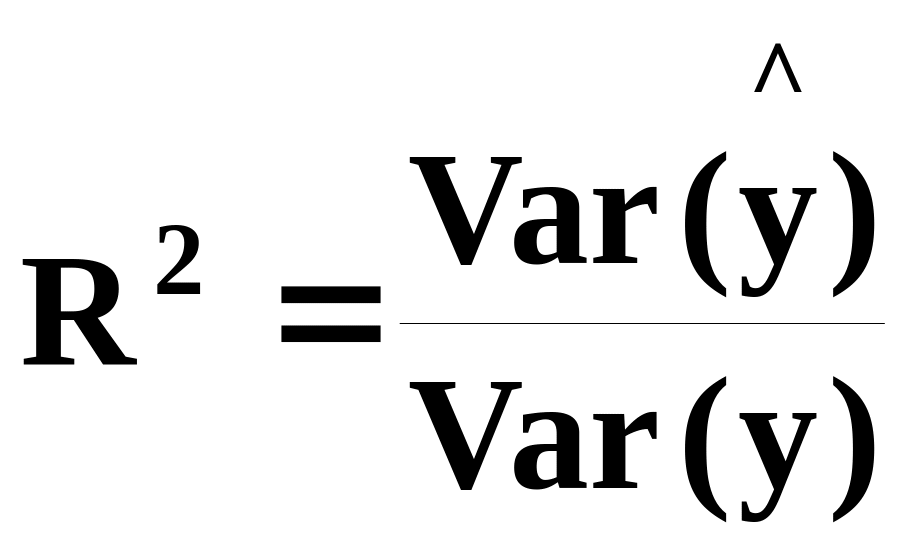 ,
что равносильно
,
что равносильно
![]() .
.
Максимальное
значение коэффициента
равно единице. Это происходит в том
случае, когда линия регрессия точно
соответствует всем наблюдениям, так
что
![]() для всех i
и все остатки равны нулю. Тогда
для всех i
и все остатки равны нулю. Тогда
![]() ,
,
![]() и
и
![]() =1.
Если в выборке отсутствует видимая
связь между у и х, то коэффициент
будет близок
к нулю.
=1.
Если в выборке отсутствует видимая
связь между у и х, то коэффициент
будет близок
к нулю.
Пример 3.1.
Для 13 клиентов спортивного отдела
магазина зафиксирована сумма покупки
![]() (в у.е.) и время разговора с продавцом
(в у.е.) и время разговора с продавцом
![]() (в мин.). Данные представлены в таблице
3.1.
(в мин.). Данные представлены в таблице
3.1.
Таблица 3.1
|
40 |
50 |
60 |
80 |
100 |
110 |
120 |
130 |
150 |
160 |
180 |
200 |
310 |
|
14 |
14 |
17 |
19 |
17 |
20 |
24 |
22 |
25 |
24 |
18 |
20 |
26 |
Т р е б у е т с я:
1) Оценить с помощью МНК параметры линейного регрессионного уравнения, предположив, что переменная «длительность разговора с продавцом» объясняется переменной «величина покупки».
2) Оценить с помощью МНК параметры линейного регрессионного уравнения, предположив, что переменная «величина покупки» объясняется переменной «длительность разговора с продавцом».
3) Нарисовать диаграмму рассеяния величин ( , ) и обе линии регрессии. Объяснить, почему, если поменять экзогенную и эндогенную переменные местами, как правило, получаются различные уравнения регрессии.
Решение
1.Для оценки
параметров линейного регрессионного
уравнения
![]() рассчитаем сначала
рассчитаем сначала
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
![]() и
и
![]() .
.
С учетом этого
![]() ;
;
![]()
В целом, получаем
![]() (3.1)
(3.1)
2.Оценим теперь
параметры линейного регрессионного
уравнения
![]() .
.
![]() ;
;
![]()
таким образом,
![]() (3.2)
(3.2)
3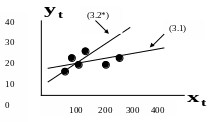 .
Для того чтобы можно было сравнить
уравнения (3.1) и (3.2), выразим y
из уравнения (3.2) и получим
.
Для того чтобы можно было сравнить
уравнения (3.1) и (3.2), выразим y
из уравнения (3.2) и получим
![]() (3.2*)
Сравнение коэффициентов уравнений
(3.1) и 3.2*) показывает, что уравнения (3.1)
и (3.2) различны (рисунок 3.1).
(3.2*)
Сравнение коэффициентов уравнений
(3.1) и 3.2*) показывает, что уравнения (3.1)
и (3.2) различны (рисунок 3.1).
Рисунок
3.1-Диаграмма рассеяния величин
и
![]() графики уравнений регрессии (3.1) и (3.2*)
графики уравнений регрессии (3.1) и (3.2*)
![]()
Если
рассматривать переменную у как эндогенную,
а переменную х –как экзогенную, то
основу МНК образуют величины
(разности
![]() ),
если поменять переменные местами, то
основу МНК образуют
),
если поменять переменные местами, то
основу МНК образуют
![]() (разности
(разности
![]() )(рисунок
3.2). Минимизация суммы квадратов разностей
абсцисс дает, как правило, выборочную
прямую, отличную от той, которую дает
минимизацию разностей ординат. Прямые
совпадают только в том случае, когда
все пары наблюдений лежат на одной
прямой, наклон которой не ноль.
)(рисунок
3.2). Минимизация суммы квадратов разностей
абсцисс дает, как правило, выборочную
прямую, отличную от той, которую дает
минимизацию разностей ординат. Прямые
совпадают только в том случае, когда
все пары наблюдений лежат на одной
прямой, наклон которой не ноль.

Рисунок 3.2 - Варианты измерения расстояния от точки до прямой
Задание 3.1. Дана таблица наблюдений
-
n
x
y
1
1
3
2
2
5
3
3
6
а) Составить уравнение регрессии.
б) Вычислить коэффициент детерминации.
Задание 3.2. Дана таблица наблюдений
-
i
x
y
1
-2
-5
2
2
8
3
3
11
а) Построить уравнение парной линейной регрессии.
б) Вычислить коэффициент детерминации
Задание 3.3. Дана таблица наблюдений
-
i
x
y
1
5
-5
2
4
8
3
9
11
Построить уравнение парной линейной регрессии.
Задание 3.4.
Исследуется зависимость
затрат на рекламу у
от годового
оборота х в
некоторой отрасли. Для этого собрана
информация по T
=
20 случайно
выбранным предприятиям этой отрасли о
годовом обороте xt
и соответствующих
расходах на рекламу yt
(в млн. руб.). Из
выборки получены следующие данные:
![]() = 17,3;
= 17,3;
![]() =
1,2;
=
1,2;
![]() = 944,3;
= 944,3;
![]() =9250;
=9250;
![]() =
127,2. Предполагается, что зависимость уt
от
хt
описывается
следующим уравнением: yt
= 0
+
1xt+
t
(t
=
1,...,
20).
=
127,2. Предполагается, что зависимость уt
от
хt
описывается
следующим уравнением: yt
= 0
+
1xt+
t
(t
=
1,...,
20).
Т р е б у е т с я:
1) Оценить параметры 0 и 1 с помощью МНК;
2)
Оценить
дисперсию
![]() «истинной» ошибки t;
«истинной» ошибки t;
3)Оценить дисперсии оценок a0 и а1 и их ковариацию.
Задание 3.5. Имеется выборка, состоящая из T = 6 пар наблюдений (xt, yt) :
