
- •1 Введение в эконометрику
- •1.1 Предмет эконометрики
- •1.2 Типы статистических данныx
- •1.3 Классы моделей
- •1.4 Оценивание моделей и типы зависимостей
- •1.5 Элементы математической статистики
- •1.5.1 Операция суммирования
- •1.5.2 Случайные переменные (величины)
- •1.5.3 Числовые характеристики распределения
- •1.5.4 Вероятность в непрерывном случае
- •2 Постоянная и случайная составляющие случайной переменной
- •2.1Способы оценивания характеристик случайной величины и оценки
- •3 Выборочная ковариация. Выборочная дисперсия. Коэффициент корреляции
- •3.1 Выборочная ковариация
- •3.2 Выборочная дисперсия
- •3.3 Коэффициент корреляции
- •4 Парный регрессионный анализ
- •4.1 Модель парной линейной регрессии
- •4.2 Метод наименьших квадратов (мнк)
- •4.3 Качество оценки: Коэффициент детерминации
4 Парный регрессионный анализ
4.1 Модель парной линейной регрессии
Важнейший задачей экономического анализа является установление взаимосвязей экономических переменных, что помогает при анализе их поведения [2,15].
Коэффициент корреляции показывает, что две переменные связаны друг с другом, но он не дает представления о том, каким образом они связаны.
Рассмотрим случай двух переменных и и определим существует или нет линейная связь между ними.
Проведем случайную выборку.
При
значениях
![]() наблюдаем значения
наблюдаем значения
![]() соответственно. На плоскости
соответственно. На плоскости
![]() отметим точки с координатами
отметим точки с координатами
![]() .
.
Предположим, что точки группируются вокруг некоторой прямой линии
![]()
точки не находятся точно на этой линии. Это неудивительно, т.к. помимо на поведение оказывают влияние и другие факторы.
На
переменные
![]() накладывается ряд условий. Для
описания природы связи используется
термин «регрессия».
«Регресс»
(лаг) – отклонение, движение назад.
накладывается ряд условий. Для
описания природы связи используется
термин «регрессия».
«Регресс»
(лаг) – отклонение, движение назад.
Зависимость между переменными и в генеральной совокупности можно представить как модель парной линейной регресии
![]()
где – результативная (или объясняемая, зависимая) переменная;
– факторная ( или объясняющая , независимая) переменная;
![]() и
и
![]() – неизвестные параметры модели;
– неизвестные параметры модели;
– случайный член (случайная ошибка регрессионной модели).
Величина состоит из двух составяющих:
1)
случайный составляющий
![]() ;
;
2) случайного члена .
Основные предпосылки модели парной линейной регресии:
связь между переменными и линейная;
независимая переменная может быть использована для прогноза ;
остатки нормально распределены;
для всех данных математическое ожидание равно нулю;
ошибки независимы;
Наличие случайного члена связано с воздействием на зависимую переменную у других неучтенных в данной модели факторов.
Например, нелинейность модели, наличие других переменных, неучтенных в модели; неправильный выбор объясняющей переменной, ошибки в измерениях.
Рассмотрим как комбинация этих двух составляющих определяет величину .
Пусть
объясняющая (факторная) переменная
имеет значения
![]() .
Если бы соотношение
были бы точным, то вычисленные по формуле
.
Если бы соотношение
были бы точным, то вычисленные по формуле
![]() значения
значения
![]() были бы представлены точками
были бы представлены точками
![]() ,
которые лежали бы на прямой.
,
которые лежали бы на прямой.
Наличие случайного члена приводит к тому, что в действительности значение у получается другим.
Обозначим
через
![]() ,
точки которые отражают реальные значение
(
рисунок 4.1).
,
точки которые отражают реальные значение
(
рисунок 4.1).
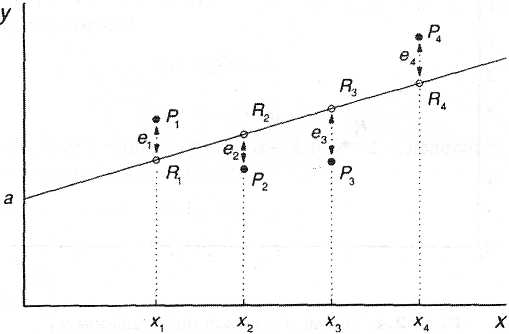
Рисунок 4.1
На
диаграмме рассеяния случайный член
![]() для точек
для точек
![]() и
и
![]() и
и
![]() для точек
для точек
![]() и
и
![]() .
.
Фактические значения параметров и , отсюда и положение точек
![]() ,
а также фактическое значение случайного
члена
неизвестны.
,
а также фактическое значение случайного
члена
неизвестны.
Рассчитать истинные значения и практически невозможно.
Можно получить только оценки этих параметров.
Задача
регрессионного анализа состоит в
получении
оценок
параметров
и
и в определении положения прямой по
точкам
![]() .
Очевидно, чем меньше значение
,
тем легче эта задача.
.
Очевидно, чем меньше значение
,
тем легче эта задача.
Пусть имеем четыре наблюдения .
На
основе выборочного наблюдения оценим
выборочное уравнение регресии (линии
регрессии)
![]() ,
где
,
где
![]() -
отрезок, отсекаемый прямой на оси
-
отрезок, отсекаемый прямой на оси
![]() ,
является оценкой
,
,
является оценкой
,
![]() – угловой коэффициент прямой, т.е.
показатель наклона линии линейной
регрессии, является оценкой
.
– угловой коэффициент прямой, т.е.
показатель наклона линии линейной
регрессии, является оценкой
.
Пусть
при
![]() вычислим
вычислим
![]() ,
соответствующей точкой на линии регрессии
будет
,
соответствующей точкой на линии регрессии
будет
![]() .
.
Разность
между фактическим и расчетным значениями
![]() называется остатком в первом наблюдении
и определяется отрезком
называется остатком в первом наблюдении
и определяется отрезком
![]() .
.
Аналогично определим остатки:
![]()
![]()
![]()
Очевидно,
что линию регрессии нужно строить так,
чтобы остатки
![]() были бы минимальными.
были бы минимальными.
При этом линия, строго соответствующая одним наблюдениям не будет соответствовать другим и наоборот.
Необходимо выбрать такой критерий подбора коэффициентов и в уравнении линии регрессии , который будет одновременно учитывать величину всех остатков.
Один
из способов решения данной проблемы
состоит в минимизации суммы
![]()
Величина
![]() зависит от выбора
и
,
так как они определяют положение линии
регрессии.
зависит от выбора
и
,
так как они определяют положение линии
регрессии.
Чем меньше , тем строже может соответствовать.
Если
![]() ,
то получено абсолютно точное соответствие,
так как это значит, что все остатки равны
нулю.
,
то получено абсолютно точное соответствие,
так как это значит, что все остатки равны
нулю.
