4.2 Метод наименьших квадратов (мнк)

Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений , линейным уравнением

где и – оценки параметров и в модели парной регресии

Пусть имеем n наблюдений

і	х	у
1 2 ... n	х1 х2 ... хn	у1 у2 ... уn

По этим данным можно построить оцененное уравнение регрессии

По этому уравнению вычислим , .

Величина является расчетным значением переменной , соответствующее .

Наблюдаемые значения не может в точности на линии регрессии, так как не совпадают с .

Остаток в –м наблюдении определяется как разность между фактическим и расчетным значениями зависимой переменной, т.е. .

Р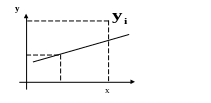 асположение линии регрессии, задаваемой уравнением определяется параметрами и . Приведем диаграмму рассеяния наблюдений и линии регрессии (рисунок 4.2).

. .

.

.

.

Рисунок 4.2

Неизвестные значения определяются методом наименьших квадратов.

Суть МНК заключается в минимализации суммы квадратов остатков

где – известные значения наблюдения (числа);

– неизвестные.

Это квадратичная функция. Необходимые условия экстремума функции заключается в равенстве нулю частных производных по и :

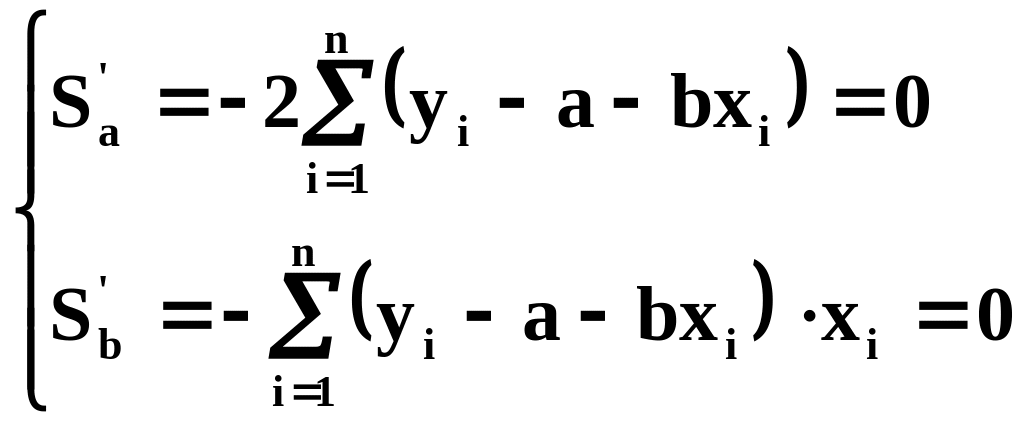
В развернутом виде эти уравнения запишутся в виде:

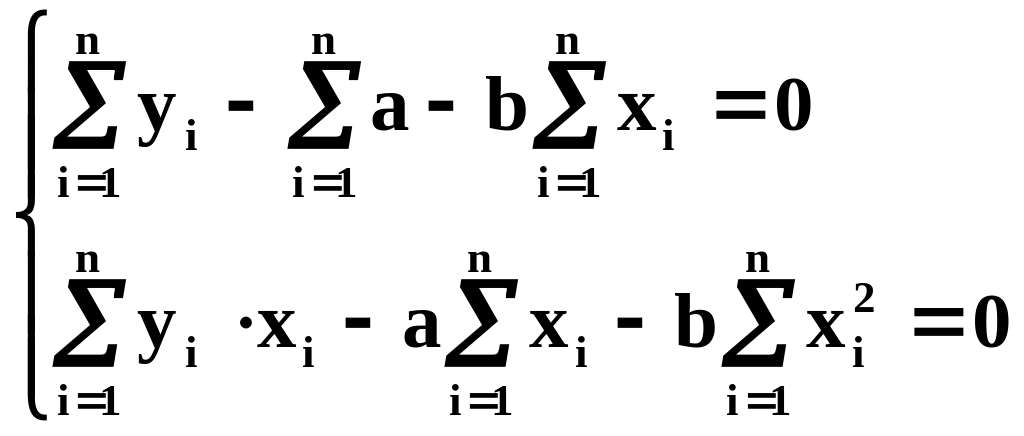
Или

, .

Решение этой системы с двумя неизвестными и :

Расчетное значение зависимой переменной или линия регрессии имеет уравнение или .

Линия регрессии проходит через точку и выполняются равенства

.

Коэффициент есть угловой коэффициент регрессии, т.е. показатель наклона линии линейной регрессиии. Он показывает, на сколько единиц в среднем изменяется переменная у при увеличении независимой переменной на единицу.

Постоянная дает прогнозируемое значение зависимой переменной при .

Это может иметь смысл в зависимости от того, как далеко находится от выборочных значений .

После построения уравнения регрессии наблюдаемые значения у можно представить как .

Остатки , как и ошибки являются случайными величинами. Однако они в отличии от ошибок наблюдаемы.

Докажем, что

Доказано, так как , ;

,

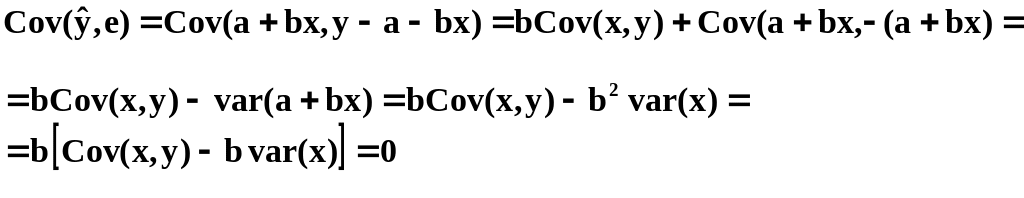
Выборочные дисперсии вычисляются по формулам:

- дисперсия наблюдаемых значений у.

- дисперсия «расчетных» значений у.

- дисперсия остатков.

Задание 4.1

Докажите, что , где коэффициент корреляции между

– их стандартные отклонения.