1.5.3 Числовые характеристики распределения

В основе математической статистики лежат понятия генеральной и выборочной совокупностей.

Генеральная совокупность – это множество всех значений (исходов) случайной величины, которые она может принять в процессе наблюдения.

Например, данные о доходах всех жителей страны.

Выборочная совокупность (выборка) – это множество наблюдений, составляющих лишь часть генеральной совокупности.

Генеральная совокупность и ее числовые характеристики

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее значений на соответствующие вероятности, то есть:

(1.5)

Пример 1.3 Дано распределение

х	4	6	7
р	0,5	0,3	0,2

Найти математическое ожидание Е(х).

Решение.

Пример 1.4. Случайная величина принимает число очков при бросании одной игральной кости. Найти математическое ожидание Е(х).

х	1	2	3	4	5	6
р	1/6	1/6	1/6	1/6	1/6	1/6

Решение.

Математическое ожидание функций дискретных случайных величин.

Пусть g(х) есть некоторая функция от х. Математическое ожидание функции g(х) вычисляется по формуле , где суммирование производится по всем возможным значениям х.

Практический расчет математического ожидания функции от х можно оформить в виде таблице 1.2:

Таблица 1.2

Х	вероятность	функция от х	функция, взвешенная по вероятности
х1	р1	g(х1)	g(х1)*р1
х2	р2	g(х2)	g(х2)* р2
…	…	…	…
хn	рn	g(хn)	g(хn)* рn
Всего

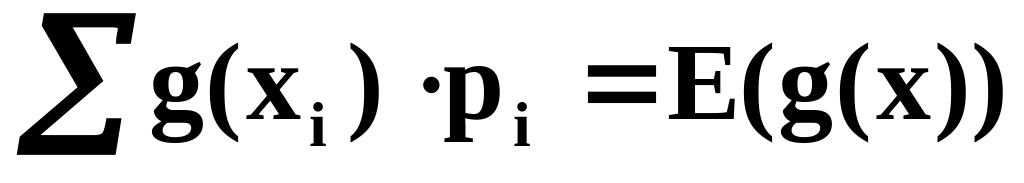
Математическое ожидание непрерывной случайной величины определяется выражением:

, (1.6)

где интегрирование осуществляется на всем интервале, в котором определяется ƒ(х)

Если g(х)- функция случайной величины x, то математическое ожидание функции g(х):

, (1.7)

где интегрирование проводится на всем интервале, в котором определена ƒ(х).

Математическое ожидание случайной величины - это среднее ее значение по генеральной совокупности, обозначается

(1.8)

Геометрически: математическое ожидание случайной величины – это центр ее распределения.

Пример 1.5. Случайная величина х задана плотностью распределения ƒ(х)=2х, в интервале (0;1), вне этого ƒ(х)=0. Найти математическое ожидание х.

Решение:

Свойства математического ожидания:

Расчет математического ожидания проводится на основании свойств, которые одинаково применимы для дискретных случайных величин и непрерывных случайных величин.

Пусть a,b – константы; х,у - случайные величины.

Свойство 1. . Математическое ожидание постоянной величины равно самой постоянной.

Cвойство 2. постоянный множитель можно выносить за знак математического ожидания.

Cвойство 3. математическое ожидание суммы случайных величин рано сумме их математических ожиданий.

Cвойство 4. .

Cвойство 5. .

Cвойство 6. Случайные величины х, у называются независимыми, если для любых значений x ,y.

Если случайные величины х и у независимы то: .

Свойство 7. Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:

Пример 1.6 Найти математическое ожидание случайной величины z если известны математические ожидания величин x и y, и если:

а) б)

Решение:

а) .

Используя, 2 и 3 свойства математического ожидания имеем:

б) .

Пусть х – случайная величина, Е(x) ее математическое ожидание. Отклонением называется разность между случайной величиной х и ее математическим ожиданием Е(x), т.е х - E(x).

Теоретической (генеральной) дисперсией случайной величины х называется математическое ожидание квадрата отклонения случайной величины х от математического ожидания .

Обозначения теоретической дисперсией: .

По определению

Если ясно, о какой переменной идет речь, то нижний индекс в и можно не указывать, т.е. и .

Из определения дисперсии получается другая более удобная формула вычисления:

.

Для дискретной случайной величины:

.

Для непрерывной случайной величины:

.

Дисперсия является мерой рассеяния случайной величины относительно средней (центра). Размерность дисперсии не совпадает с размерностью случайной величины.

Стандартным или средним квадратическим отклонением случайной величины х называется величина: .

Стандартное отклонение показывает, насколько в среднем отклоняется случайная величина в совокупности относительно центра (средней).

Положительное значение стандартного отклонения говорит о наличии прямой статистической связи, а отрицательное значение об обратной статистической связи между случайной величиной и средней (центром).

Пусть х_{1 ,}х_{2 , …,} х_n - случайные величины

.

Пример 1.7 Вычислить дисперсию и стандартное отклонение для дискретной случайной величины, заданной распределением:

х	1	3	5
р	0,3	0,5	0,2

Решение:

Математическое ожидание: .

Дисперсия:

Стандартное отклонение .

Свойства дисперсии:

1) Дисперсия постоянной равна нулю, т.е , где c – const.

2) При умножении случайных величин на константу ее дисперсия умножается на квадрат этой константы, т.е .

3) Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых, т.е .

4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е .

5) , где a и b- числа.

6) Дисперсия (биномиального распределения) появления события А в n независимых испытаниях, в каждом из которых вероятность появления события постоянно и равно р, т.е ,

где n-число независимых испытаний;

p- вероятность появлений события в одном испытании;

q=1-р вероятность непоявления события в одном испытании.

Заметим, что математическое ожидание: и дисперсия это числовые характеристики генеральной совокупности (числа), а не функции.

Запись будет в дальнейшем означать, что математическое ожидание равно , а дисперсия равна .

Пример 1.8 Известны дисперсии двух независимых случайных величин

, . Найти дисперсию следующих величин: a) D(x-2), б)D(5x-2y).

Решение.

а) .

б) .

Нормальное распределение случайной величины x характеризуется лишь двумя параметрами: средним значением и дисперсией . Обозначается как .

График плотности нормального распределения имеет колоколообразный симметричный вид (рисунок 1.5):

Рисунок 1.5

Максимум этой функции находится в точке , а разброс относительно этой точки определяется параметром , тем более острый и высокий максимум .

Вероятность того, что отклонение нормальной случайной величины от среднего по модулю меньше , есть

,

Где - функция Лапласа.

Нормальное распределение, для которого , т.е. называется стандартным нормальным распределением.

Используя свойства, можно установить, что, если , то случайная величина , т.е. имеет вид распределение по стандартному нормальному закону. Вероятность для через вычисляется по формуле .

Для стандартного нормального распределения составлены таблицы.

Выборочная совокупность и ее числовые характеристики

Пусть из генеральной совокупности с распределением извлекается выборка объема. Считаем, что выборочные наблюдения х_{1 ,}х_2,…, х_n независимы и имеют одинаковые распределения[5,7,17]

Выборочной средней называется среднее арифметическое значение случайной величины в выборке, т.е.

Выборочной дисперсией (вариацией) называется .

или среднее арифметическое квадратов отклонения случайной величины от среднего значения, т.е. .

Свойства выборочной дисперсии

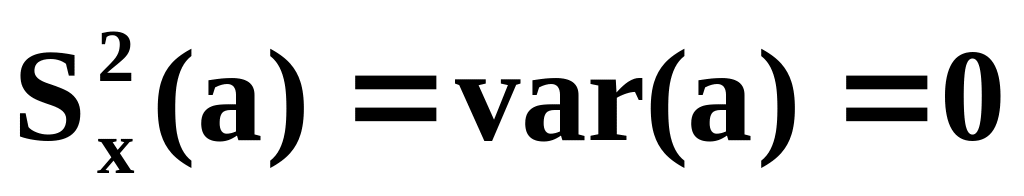1. , a – const;

2) , b-const;

3)

Значение и являются числовыми характеристиками выборочной совокупности.

Для разных выборок, взятых из одной и той же генеральной совокупности, выборочные средние и выборочные дисперсии будут различны, то есть выборочные характеристики являются случайными величинами.

Из условия, что выборочные наблюдения х_{1 ,}х_2,…, х_n независимы и имеют одинаковые распределения вытекают следующие соотношения:

Центральная предельная теорема закона больших чисел устанавливает, что распределение средней выборочной при достаточно большом является нормальным, т.е. , при этом , .
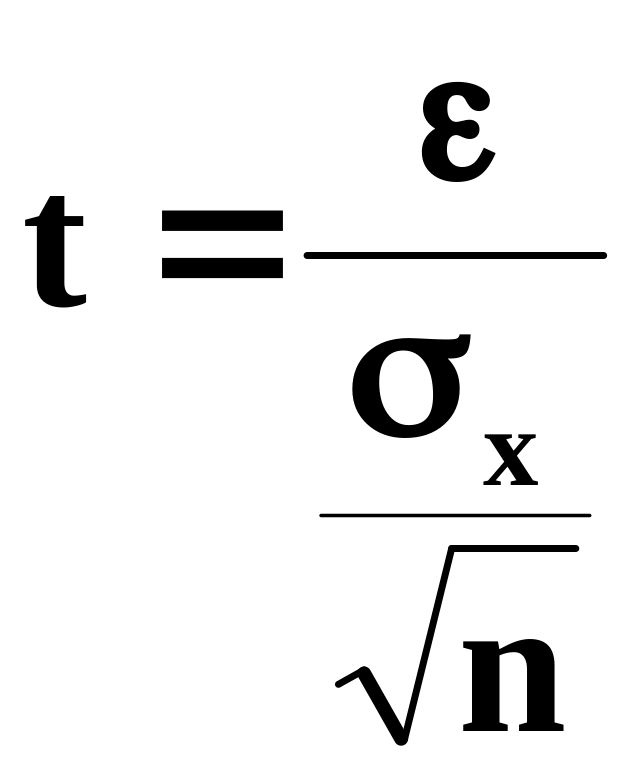