18

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ

«ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ»

КАФЕДРА ЭЛЕКТРОННОЙ ТЕХНИКИ

Методические указания к курсовой работе

по дисциплине «Квантовая и оптическая электроника»

«Матричный метод оценки характеристик оптического резонатора и параметров лазерного излучения»

МОСКВА 2010 ГОД

ВВЕДЕНИЕ

Лазеры применяются уже почти пол века, и сфера их использования быстро расширяется. Замечательные свойства луча находят многочисленные, порой самые неожиданные применения в научных исследования, технических разработках, а также в различных отраслях промышленности. В связи с этим быстро растет число специалистов самых разнообразных профилей, которым так или иначе приходится работать с лазерами, а также конструировать простейшие оптические системы фокусировки и преобразования лазерных пучков. Матричные методы расчета во многом аналогичны широко известным методам, которые уже давно используются в инженерной практике при расчетах приборов в диапазоне СВЧ и электрических схем на основе четырехполюсников. В рамках этих методов полная матрица системы записывается в виде произведения матриц составляющих ее элементов. С помощью этих матриц можно решать важные задачи (в квазиоптическом приближении) многочисленные практические задачи лазерной оптики, например, вычислять параметры пучка на выходном зеркале, рассчитывать линзовые оптические волноводы, оптимальную фокусировку лазерного излучения на мишени и т.д.

1. Введение в матричные исчисления

В данном разделе изучаются элементарные основы матричных исчислений, которые позволят понять дальнейшее изложение материала. Основное внимание будет уделено изучению квадратных матриц размера 2х2.

Рассмотрим, каким образом возникает понятие матрицы. Предположим, что мы имеем систему линейных уравнений

(1)

где A, B, C, D – известные константы, x, y – переменные величины. Эти уравнения позволяют вычислить U и V, если известны x и y. Во многих случаях оказывается удобным отделить постоянные величины от переменных. При этом два уравнения можно записать в виде одного соотношения следующим образом:

(2)

Каждая из групп символов, заключенная между парой вертикальных скобок, рассматривается как единое целое и называется матрицей. Величины

представляют собой матрицы – столбцы, или векторы – столбцы.

Матрица

,

которая состоит из двух строк и двух столбцов, называется квадратной матрицей второго порядка (размера 2х2). Матрица – строка, или вектор – строка, записываются в виде [P Q], в ней отдельные символы – матричные элементы – расположенные горизонтально на одной строке.

Матричное произведение. Если заданы две матрицы

,

тогда матричное произведение имеет вид

.

(3)

При перемножении матриц необходимо учитывать следующие условия:

• должен соблюдаться порядок сомножителей (M₁M₂M₂M₁), т.е. произведение матриц некоммутативное;

• можно перемножить матрицы М₁ и М₂, тогда и только тогда, когда число столбцов в первом сомножителе (матрица М₁) такое же, как число строк во втором сомножителе (матрица М₂), в этом случае матрицы М₁ и М₂ называются согласованными.

Если мы хотим найти произведение трех матриц М₁, М₂, М₃, то можно поступить двумя способами:

• найти произведение (М₂ М₃), а затем умножить его слева на М₁;

• найти произведение (М₁ М₂), а затем умножить его справа на М₃.

При условии, что мы сохраняем порядок расположения матриц, эти два способа дают одинаковый результат, М₁М₂М₃=М₁(М₂М₃)=(М₁М₂)М₃. Таким образом, хотя произведение матриц не обладает свойством коммутативности, тем не менее, ассоциативный закон для него справедлив. Обобщая этот закон на большое число матриц, нетрудно показать, что для произведения четырех матриц М₁М₂М₃М₄=М₁(М₂М₃)М₄=(М₁М₂М₃)М₄.

Нулевая матрица. Матрица, в которой все элементы равны нулю, называется нулевой матрицей. Нулевая матрица второго порядка имеет вид:

.

(4)

При умножении любой матрицы, имеющей в качестве первого или второго сомножителя нулевую матрицу (согласованной формы), мы получаем нулевую матрицу.

Диагональная матрица (). Матрица, в которой элементы главной диагонали могут иметь любые значения, а недиагональные элементы равны нулю, называется диагональной матрицей.

Единичная матрица. Диагональная матрица, в которой элементы главной диагонали равны единице, называется единичной матрицей. Единичная матрица второго порядка имеет вид

.

(5)

Основное свойство единичной матрицы второго порядка: любая матрица из двух строк, умноженная на нее слева, и любая матрица из двух столбцов, умноженная на нее справа, в результате остаются неизменными.

Сложение и вычитание матриц. При условии, что две матрицы М₁ и М₂ имеют одинаковое число строк и столбцов, их сумма (или разность) получается простым сложением (или вычитанием) любых двух соответствующих матричных элементов. Матрицы подчиняются дистрибутивному закону: М₁ (М₂+М₃)=М₁М₂+М₁М₃.

Если мы одну и ту же матрицу сложим саму с собой  раз, то каждый из матричных элементов окажется умноженным на одно и то же число (или скалярную величину) . Такую операцию называют иногда умножением матрицы на скаляр. Тот же результат можно получить перемножением матриц, если умножить матрицу справа или слева на диагональную матрицу I, все диагональные элементы которой равны .

Транспонированная матрица. Матрица, полученная в результате замены строк на соответствующие столбцы в некоторой матрице М, называется транспонированной матрицей по отношению к М и обозначается М^Т. Если матрица М имеет m строк и n столбцов, то транспонированная к ней матрица М^Т состоит из n строк и m столбцов.

Существует важная теорема об умножении транспонированных матриц: матрица, транспонированная по отношению к произведению двух матриц, равна произведению их транспонированных матриц, выполненному в обратном порядке, (М₁М₂)^Т=М₂^ТМ₁^Т. Используя ассоциативное свойство матричного умножения, нетрудно показать, что (М₁М₂М₃)^Т = ((М₁М₂)М₃)^Т = М₃^Т(М₁М₂)^Т= М₃^ТМ₂^ТМ₁^Т.

Определитель. Для любой квадратной матрицы существует единственное число или величина, которая называется ее определителем. Определитель матрицы М размером 2х2 имеет вид:

.

(6)

Правило для вычисления определителя квадратной матрицы размером 2х2 – найти произведение двух элементов главной диагонали и вычесть из него произведение остальных двух элементов.

Теорема об определителях - определитель произведения двух и более квадратных матриц равен произведению их определителей, т.е. det(M₁M₂)=det(M₁)det(M₂). Отметим, что для определителей порядок перемножения матриц не имеет значения.

Для определителя матрицы характерны следующие особенности

• если определитель матрицы равен нулю, такая матрица называется вырожденной (или особенной), в противном случае – невырожденной (или неособенной);

• если определитель матрицы размером 2х2 равен единице, такую матрицу называют унимодулярной.

Обратная матрица. Если матрица М не вырожденная, то существует одна и только одна обратная ей матрица R, обладающая тем свойством, что как произведение (MR), так и произведение (RM) равно единичной матрице I того же порядка. Эту матрицу будем обозначать через М^-1.

Обращение матриц. Правило нахождения обратной матрицы называется обращением матрицы. Это правило состоит в том, чтобы найти присоединенную матрицу, транспонировать ее, а затем разделить на определитель.

В случае матрицы размером 2х2 присоединенная матрица получается простой взаимной заменой диагональных элементов с одновременным изменением знака правого верхнего и левого нижнего элементов.

Для матрицы

можно записать присоединенную матрицу вида

.

Найдем матрицу, транспонированную по отношению к матрице adj(M),

,

и, наконец, разделим каждый ее элемент на определитель det(M)=(AD-BC). Заметим, что определители всех трех приведенных выше матриц одинаковы.

Чтобы обратить унимодулярную матрицу 2х2, нужно поменять местами элементы, расположенные на главной диагонали, и изменить знаки двух других элементов, оставляя эти элементы на своих местах:

,

тогда

.

Чтобы получить матрицу, обратную произведению нескольких матриц, необходимо перемножить в обратном порядке матрицы, обратные отдельным сомножителям:

.

Приведение матрицы к диагональному виду. Иногда возникает необходимость выполнить одно за другим умножение на одну и ту же невырожденную матрицу М. При этом оказывается удобным найти диагонализирующую матрицу F, т.е. матрицу, преобразующую исходную к диагональному виду:

,

(7)

где  - диагональная матрица, F^-1 – матрица, обратная к F.

Если допустить, что матрицы F и  существуют, то F^-1 F=I, тогда

.

Аналогично,

.

В общем случае

.

(8)

Таким образом, если преобразование к диагональному виду найдено, то N-я степень исходной матрицы получается простым возведением диагональной матрицы в N-ю степень, причем все, что мы должны сделать, - это заменить каждый элемент главной диагонали  величиной ^N.

Диагональные элементы ₁, ₂, … _r, … матрицы  называют характеристическими корнями или собственными значениями исходной матрицы F, а отдельные столбцы диагонализирующей матрицы F называют соответственно ее характеристическими векторами или собственными векторами. Для матрицы 2х2 существуют только два собственных значения

Собственные значения и собственные векторы унимодулярной матрицы. Если мы хотим привести квадратную матрицу М к диагональному виду, то следует начать с определения собственных значений ₁, ₂, … и т.д. Для этого обычно решают характеристическое уравнение матрицы М:

.

(8)

В случае унимодулярной матрицы размера 2х2:

.

Согласно условию, det(M)=(AD-BC)=1, характеристическое уравнение для двух значений  можно упростить:

.

Из уравнения видно, что два решения ₁, ₂ должны удовлетворять равенствам ₁+₂=A+D и ₁₂=1. Решая квадратное уравнение, находим

.

(9)

Величину (A+D), т.е. сумму диагональных элементов, называется след матрицы. Если след матрицы принимает значение от 2 до -2, то два собственных значения удобно переписать в виде функции угла , выбирая его, так, чтобы он изменялся в пределах от 0 до . Таким образом, можно записать

.

(10)

Тогда мы получим следующие равенства

(11)

В уравнении (11):

.

Наоборот, если (A+D)>2 или (A+D)<-2, то можно выбрать такую положительную величину t, что (A+D)=+2ch(t) – в первом случае, или (A+D)=-2 ch(-t) – во втором случае, где ch(t) – гиперболический косинус от t. При этом собственные значения записываются виде:

• если (A+D)>2, тогда ₁=exp(+t) и ₂=exp(-t),

• если (A+D)>-2, тогда ₁= -exp(+t) и ₂= -exp(-t).

Чтобы завершить процесс приведения матрицы к диагональному виду, необходимо определить диагонализирующую матрицу F:

,

и обратную ей матрицу F^-1:

.

Итак, окончательное преобразование, приводящее матрицу к диагональному виду, имеет вид

,

(12)

где AD-BC=1, а ₁ и ₂ таковы, что ₁₂=1 и ₁+₂=A+D.
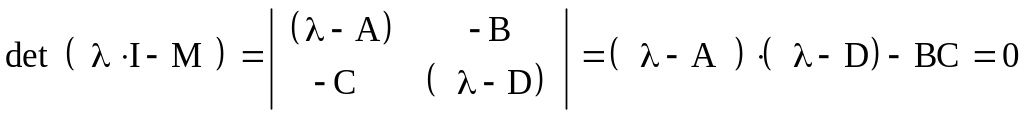
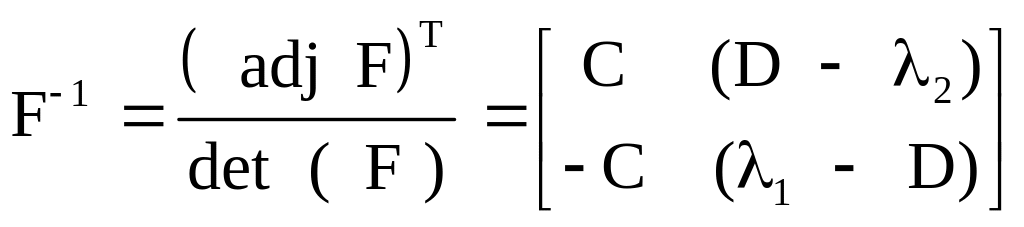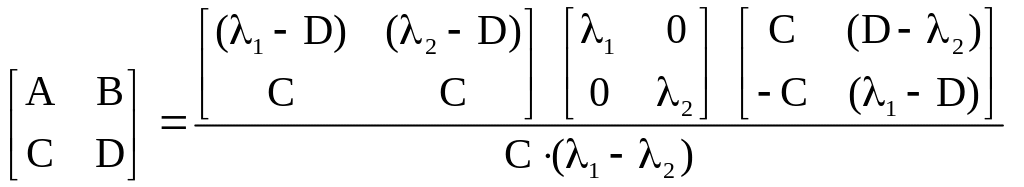