9698

Следовательно, искомый предел равен

Лекция 22. Исследование функций и построение их графиков

В аналитическом выражении, которым чаще всего бывает задана функция, содержится вся информация о её свойствах. График функции делает эти свойства легко обозримыми. Поэтому нужно уметь строить график функции по формуле, которой она задана. Самый простейший приём – это построение «по точкам». Однако он требует большого объёма вычислений и при этом могут быть потеряны характерные особенности исследуемой функции. Приёмы исследования, основанные на дифференциальном исчислении, позволяют именно эти особенности и уловить. Так, например, один факт существования производной функции в точке x0 даёт возможность линеаризовать функцию в окрестности этой точки. Дифференцируемость функции, как мы выяснили ранее, равносильна представлению её приращения в виде

y = f ′(x0 ) x + α( x) ,

где α( x) – бесконечно малая более высокого порядка, чем x . Заменяя

мы заменяем в окрестности точки x0 кривую y = f (x) касательной к ней в этой точке. Нельзя ли это приближённое равенство превратить в точное? Такое равенство, выражающее приращение дифференцируемой функции через приращение её аргумента, было получено Лагранжем (1736-1813гг).

22.1. Формула Лагранжа имеет вид

За знак равенства в ней мы «заплатили» тем, что не знаем точного положения точки ξ. Эту формулу называют также формулой конечных

приращений.

150

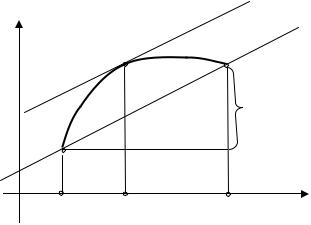
Из (22.1) следует, что на интервале (x0 , x) существует точка ξ, в которой

т.е. касательная в этой точке параллельна прямой AB (см. рис. 22.1). Из рисунка видно, что ξ является абсциссой точки P , полученной перемещением прямой AB параллельно себе. Формулу конечных приращений или формулу Лагранжа (22.1) мы будем неоднократно применять в дальнейшем.

f ( x) − f ( x0 )

A α

22.2. Признак монотонности функции. Применим формулу Лагранжа к исследованию поведения функции на некотором промежутке ( a , b ) . Напомним, что функция называется возрастающей в этом промежутке, если для любых значений x1 < x2 выполняется неравенство f (x1 ) < f (x2 ) . Выясним, каков же признак того, что функция возрастает.

Пусть производная функции положительна во всех точках

т.е. f (x) – возрастающая функция. В предположении, что производная неотрицательна ( f ′(x) ³ 0) , получим, что функция – неубывающая в этом промежутке, т.е. f (x2 ) ³ f (x1 ) .

151

Аналогичным образом можно получить признаки убывающей и невозрастающей функций: f ′(x) < 0 и f ′(x) ≤ 0 .

Геометрически эти признаки означают, что в точках возрастания функции касательная к кривой составляет острый угол с положительным направлением оси абсцисс, а в точках убывания – тупой. В качестве примера найдем промежутки возрастания и убывания функции

Рис. 22.2

Следовательно, в промежутке (−∞,0) эта функция возрастает, а в промежутке (0,∞) – убывает.

22.3. Экстремумы. Под экстремумом функции в точке понимают её

неравенство

f (x) ≤ f (x0 ) , ( f ( x) ³ f ( x0 ) ) .

Как находить экстремумы, зная аналитическое выражение функции? Заметим, что точки экстремумов разделяют интервалы возрастания и убывания функции (точки максимумов) и наоборот (точки минимумов). Исходя из приведенных выше условий монотонности функции, естественно предположить, что в точках экстремумов производная функции обращается в ноль или не существует. Для дифференцируемых функций имеет место следующее.

Необходимое условие экстремума. Пусть функция имеет конечную производную в (a,b) и x0 – точка максимума (для определенности). Тогда

152

производная в этой точке равна нулю f ′(x0 ) = 0 , т.е. касательная в точке

f ′(x0 ) = 0

x0

Рис. 22.3

Следующий пример показывает, что обратное утверждение не верно. Так, для функции y = x3 производная в начале координат равна нулю, касательная совпадает с осью абсцисс, но экстремума в этой точке нет.

x

Рис. 22.4

Другие точки, в которых могут быть экстремумы, это точки, в которых производная либо не существует, либо обращается в бесконечность. В совокупности со стационарными эти точки называют критическими. Примеры критических точек такого рода дают функции

y = x и y = 3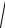 x2 .

153

Необходимые условия позволяют выделить точки, «подозрительные» на экстремум. Далее для каждой из них следует выяснить, есть ли экстремум в данной точке и, если есть, то каков он. Для этого существует следующие условия.

Достаточные условия экстремума. Если при «переходе» слева направо через критическую точку производная меняет знак с плюса на минус, то в этой точке максимум, а если с минуса на плюс, то минимум. Для дважды дифференцируемой функции это эквивалентно тому, что, если

то это точка минимума.

В самом деле, смена знака производной означает переход функции от возрастания к убыванию или наоборот, что соответствует экстремуму. Для дважды дифференцируемой функции смена знака иторой производной, например, с плюса на минус при переходе через стационарную точку означает, что первая производная функции убывает в некоторой окрестности этой точки. Следовательно, производная от первой производной, т.е. вторая производная f ′′(x) , должна быть отрицательной в этой окрестности, а значит и в самой точке, т.е. f ′′(x0 ) < 0 (см. рис. 22.6).

Верно и обратное: если вторая производная отрицательна в точке x0 , то она, будучи непрерывной в этой точке, отрицательна в некоторой её окрестности. Значит, существует окрестность точки x0 , где её производная

154

Рис. 22.8

Лекция 23. Исследование функций и построение их графиков

(продолжение)

23.1. Выпуклость. Понятие выпуклости – одно из важнейших понятий всей математики. Мы ограничимся применением этого понятия к исследованию выпуклости графика функции. Обратимся к рисунку.

y

f2 ( x)

f1 ( x)

x

Рис. 23.1

Пусть в промежутке (a,b) заданы две дифференцируемые функции. Их графики – это непрерывные кривые, имеющие в каждой точке касательную. Обе функции возрастают в этом промежутке. Но график одной из них обращен «горбом» вниз, а у другой – в противоположную сторону. Это свойство кривой называют выпуклостью. Как описать это свойство в математических терминах?

В математике есть понятие выпуклой функции, применяемое к более широкому классу функций, чем класс дифференцируемых функций. Мы определим это понятие именно для дифференцируемых функций. Будем называть функцию y = f (x) выпуклой (вниз) в промежутке (a,b) , если её график лежит выше касательной в любой точке из этого промежутка

(см. рис. 23.2).

В противном случае функцию называют вогнутой (выпуклой вверх). Аналитически это свойство выразится следующим неравенством

f (x) ³ f ′(x0 )(x - x0 ) + f (x0 ) = Y (x) ,

правая часть которого представляет собой значение ординаты касательной.

156

Если же точка x расположена правее точки x0 (рис. 23.4), то картина будет следующей:

Поэтому график этой функции обращён выпуклостью вниз при отрицательных значениях аргумента и выпуклостью вверх при его положительных значениях.

Рис. 23.5

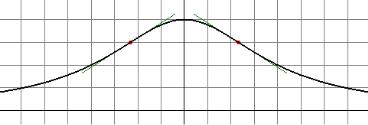
23.2. Точки перегиба. Точки графика функции, в которых направление выпуклости меняется на противоположное, называют точками перегиба. Например, у синусоиды это точки пересечения её графика с осью абсцисс. Необходимым условием существования точки перегиба графика дважды дифференцируемой функции является равенство нулю её второй производной в некоторой точке, а достаточным – перемена

158

Для этой функции имеем

Следовательно, точками перегиба могут быть только точки

При переходе через каждую из них вторая производная меняет знак, значит эти точки – точки перегиба (см. рис. 22.2).

При построении графиков полезно вычислить значение первой производной в точке перегиба, дающее направление касательной,

производная может и не существовать, что видно на графике следующей функции

23.3. Асимптоты. Иногда кривая, имеющая бесконечную ветвь, при удалении её точек в бесконечность «как бы выпрямляется» и приближается к некоторой прямой. Эту прямую называют асимптотой кривой (греч. asymptotos – несливающаяся). Если авторы этого термина подчеркивали то, что кривая не сливается с прямой, то мы обращаем внимание на то, что расстояние точки кривой (x, f (x)) до прямой – асимптоты стремится к нулю при движении точки вдоль кривой к бесконечности. Пример кривой, имеющей асимптоты, даёт график функции y = 1 x

159