
9698
.pdf
вектору |
4 |
. Тогда |
|
|
|
2 |
>1, 1, 1? |
|
|
|
Удобнее находить проекцию на вектор |
|
|
|
, коллинеарный |
||||||
|
|
|
|
|
|
|
|1 1 8 1| |
|
||
|
|
- ПрE |
|
2 · |
|
I 0.58. |
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
√3 |
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Лекция 13. Взаимное расположение прямых и плоскостей
13.1. Угол между прямыми в пространстве. Пусть заданы две прямые L1 и L2 своими каноническими уравнениями
|
|
|
|
|
|
L : |
|
x − x1 |
|
= |
y − y1 |
|
= |
z − z1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
m1 |
|
|
n1 |
|
|
|
p1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
L : |
x - x2 |
= |
y - y2 |
|
= |
z - z2 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
m2 |
|
|
n2 |
|
|
|
p2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Если |
m1 |
= |
n1 |
= |
p1 |
, что означает коллинеарность направляющих векторов |
||||||||||||||
m2 |
n2 |
p2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S1 ={m1, n1, p1} |
и S2 ={m2 , n2 , p2}, то прямые L1 и L2 параллельны и угол |
|||||||||||||||||||
между ними полагают равным нулю. Параллельные прямые, очевидно, принадлежат одной плоскости.
Под углом между пересекающимися прямыми будем понимать угол
ϕ между их направляющими векторами |
S1 ={m1, n1, p1} |
и S2 ={m2 , n2 , p2}, |
|||||||||||||||||||
если он острый, и угол α = π − ϕ в противном случае. Следовательно, |
|||||||||||||||||||||
cos a =| cos j |= |
|< S1 |
, S2 >| |
= |
|
| m1 × m2 + n1 × n2 + p1 × p2 |
| |
|
. |
(13.1) |
||||||||||||
|
UUR |
|
× |
UUR |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
S |
|
S |
2 |
|
|
|
m 2 + n 2 + p 2 × m |
2 + n 2 |
+ p 2 |
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
1 |
1 |
|
2 |
2 |
2 |
|
|
|
|
Прямые, не лежащие в одной плоскости, называются |
|||||||||||||||||||||
скрещивающимися прямыми. Определим понятие угла |
между |
||||||||||||||||||||
скрещивающимися |
прямыми. Под углом |
α |
между двумя прямыми L1 и |
||||||||||||||||||
L2 будем |
понимать |
наименьший |
из углов |
между |
пересекающимися |
||||||||||||||||
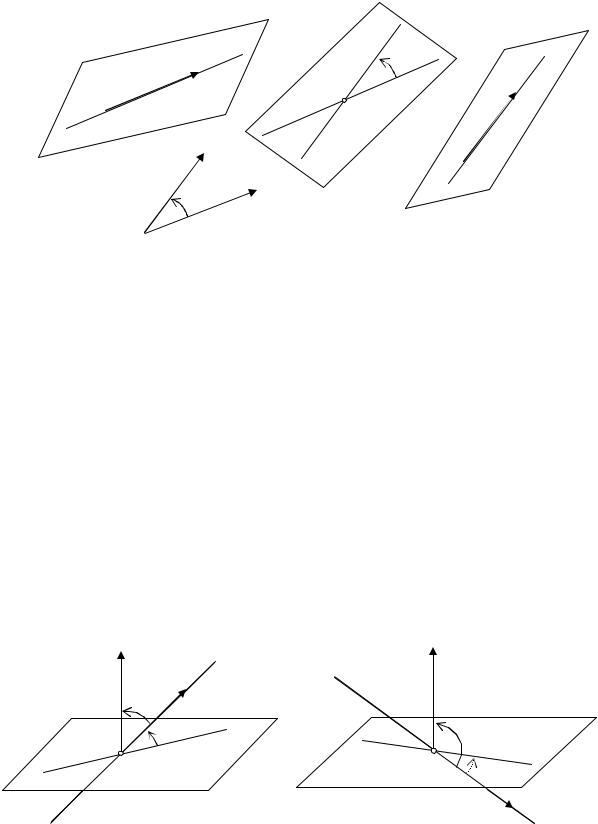
прямыми |
L ′ и |
L ′ |
, им параллельными (см. рис.13.1). |
|
|
|
|
||||||||||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90
|
L ′ |
α |
|
2 |
|
S1 |
L |
L2 |
|
1 |
L ′ |
|
|
|
|
|
1 |
S2
S2
ϕ
S1
Рис. 13.1
В частности, условие перпендикулярности двух прямых имеет
вид
L1 L2 m1m2 + n1n2 + p1 p2 = 0 .
13.2. Угол между прямой и плоскостью. Найдем теперь угол между прямой
|
L : |
x − x0 |
|
= |
y − y0 |
= |
z − z0 |
|
(13.2) |
|
m |
|
p |
||||||
|
|
|
n |
|
|||||
и плоскостью П : Ax + By + Cz + D = 0 . |
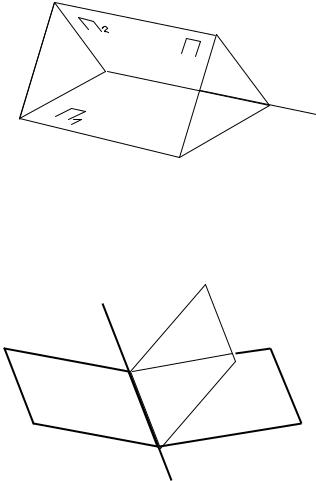
Напомним, что под углом между |
||||||||
прямой и плоскостью понимают наименьший положительный угол α |
|||||||||
между проекцией |
′ |
|
L на плоскость |
П и прямой L (см. рис. |
|||||
L прямой |
|
||||||||
13.2). |
|
|
|
|
|
|
|
|
|
N |
|
L |
|
|
|
L |
N |
||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
ϕS
α |
L′ |
ϕ |
|
′ |
|
|
|
L |
|
|
α |
|
|
S |
|
Рис. 13.2 |
|
Вычисление угла α |
можно свести к вычислению угла ϕ между |
|
направляющим вектором |
S = {m,n, p} прямой |
L и нормальным к |
|
91 |
|

плоскости |
П вектором |
N = {A, B,C}. |
В случае острого угла 0 < ϕ < π / 2 |
|||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
sinα = cosϕ = |
< N , S > |
|||||||
|
|
UUR UR . |
||||||||
|
|
|
|
|
|
| N | ×| S | |
||||
В случае тупого угла |
π / 2 < ϕ < π , так как |
j = π + a (см. рис. 13.2), |
||||||||
|
sin a = sin(j - π) = -cos j . |
|
|
2 |
|
|
||||
получим |
Таким образом, для вычисления |
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
угла между прямой и плоскостью получаем формулу |
||||||||||
|
sin a =| cos j |= |
|
|
| mA + nB + pC | |
||||||
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|||
|
|
+ B2 |
+ C 2 × |
|
||||||
|
|
|
|
A2 |
m2 + n2 + p2 |
|||||
В частности, условие перпендикулярности и условие параллельности прямой и плоскости имеют вид
L П |
|
A |
= |
B |
= |
C |
; |
m |
|
|
|||||
|
|
|
n p |
||||
L || П |
Am + Bn + Cp = 0 . |
||||||
В последнем случае, если дополнительно выполняется равенство
Ax0 + By0 + Cz0 + D = 0 ,
которое означает, что точка (x0 , y0 , z0 ) прямой L принадлежит плоскости П , то прямая лежит в этой плоскости. Таким образом, принадлежность прямой, заданной каноническими уравнениями (13.2), плоскости П : Ax + By + Cz + D = 0 определяется выполнением условий
{Am + Bn + Cp = 0
Ax0 + By0 + Cz0 + D = 0 .
Если прямая L задана как линия пересечения двух плоскостей
A1 x + B1 y + C1 z + D1 = 0
A2 x + B2 y + C2 z + D2 = 0 ,
то ее направляющий вектор может быть получен как векторное произведение нормальных векторов этих плоскостей (см. рис. 12.3), т.е.
92

S= N1 ´ N2 ,
изадача нахождения угла между прямой и плоскостью сводится к
предыдущей. В этом случае
|
|
|
< N ´ N |
, N > |
(N , N |
, N ) |
|
|
|
||||||||||||
sin j = |
R |
1 |
|
R |
2 |
|
R = |
R |
|
1 R 2 |
|
R |
. |
|
|||||||
´ |
|
|
|
|
|||||||||||||||||
|
|
|
| N1 |
N2 | ×| N | |
| N1 |
|
´ N2 | ×| N | |
|
|||||||||||||
|
|
|
|
|
|
|
13.3. |
|
|
|
|
Пересечение |
прямой с |
||||||||
|
|
|
плоскостью. Вычислим теперь координаты |
||||||||||||||||||
|
|
|
точки |
|
|
|
|
|
|
пересечения |
прямой |
||||||||||
|
|
|
L : |
x − x0 |
|
= |
y − y0 |
|
= |
z − z0 |
|
|
и |
плоскости |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
n |
|
|
|
p |
|
|
|
|
|
|
|
|
П : Ax + By + Cz + D = 0 |
при условии, что они |
|||||||||||||||||
|
|
|
пересекаются. Перейдём от канонических |
||||||||||||||||||
|
|
|
уравнений прямой к параметрическим |
||||||||||||||||||
x− x |
|
|
y− y |
|
|
z − z |
|
|
|
|
|
x = mt + x |
|
||||||||
= |
|
= |
0 |
=t |
|
|
|
|
|
0 |
|
||||||||||
0 |
|
|
0 |
|
|
|
y =nt |
+ y0 |
|
||||||||||||
m |
|
n |
|
|
p |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+z0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = pt |
|
|||||
Найдем значение параметра t1 , при котором соответствующая точка прямой принадлежит плоскости, т.е. удовлетворяет уравнению
A(mt + x0 ) + B (nt + y0 ) + C ( pt +z0 ) + D = 0
или, что тоже,
( Am + Bn + Cp)t = -( Ax0 + By0 + Cz0 + D) . |
(13.2) |
Если Am + Bn + Cp = 0 и Ax0 + By0 + Cz0 + D ¹ 0 , то это уравнение не имеет решений. Эти условия соответствуют тому, как мы выяснили выше, что прямая и плоскость параллельны и, следовательно, не пересекаются. Если Am + Bn + Cp = 0 и Ax0 + By0 + Cz0 + D = 0 , то уравнение (13.2) имеет бесчисленное множество решений, т.е. прямая принадлежит плоскости. И, наконец, если Am + Bn + Cp ¹ 0 , то
t1 |
= - |
Ax0 |
+ By0 |
+ Cz0 |
+ D |
|
|
|
|
|
. |
||
|
|
|
|
|||
|
|
Am + Bn + Cp |
||||
Подставим это значение в параметрические уравнения прямой и найдем x1, y1, z1 – координаты точки пересечения прямой L с плоскостью П .
Если прямая L задана как линия пересечения двух плоскостей
93
A1 x + B1 y + C1 z + D1 = 0
A2 x + B2 y + C2 z + D2 = 0 ,
а плоскость задана уравнением Ax + By + Cz + D = 0 , то координаты точки их пересечения находим, решая следующую систему трех линейных уравнений:
Ax + By + Cz + D = 0 |
|||
|
|
|
|
A1x + B1 y + C1z + D1 = 0 . |
|||
A x + B y + C |
2 |
z + D = 0 |
|
2 |
2 |
2 |
|
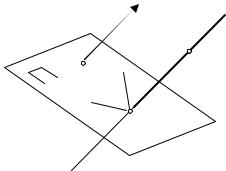
Здесь возможны варианты. Если определитель матрицы этой системы не равен нулю, то искомая точка пересечения единственна и находится, например, по правилу Крамера. Если определитель матрицы этой системы равен нулю, что означает компланарность нормальных векторов к этим плоскостям, то система может быть несовместна (см., например, рис. 13.3)
Рис. 13.3
или иметь бесчисленное множество решений, когда эти три плоскости пересекаются по одной прямой (см. рис. 13.4).
Рис. 13.4
94
Лекция 14. Другие задачи о прямых и плоскостях
Рассмотрим несколько типичных задач получения уравнений прямых или плоскостей, обладающих заданными свойствами.
Задача 1. Составить уравнения прямой L , |
проходящей через данную |
||
точку M ( x0 , y0 , z0 ) |
перпендикулярно |
к |
данной плоскости |
П : Ax + By + Cz + D = 0 . |
|
|
|
2 >, , ?
0 0 0 0
L 
Рис. 14.1
Очевидно, что в качестве направляющего вектора прямой можно взять нормальный вектор к плоскости, т.е. S = N = {A, B,C}. Отсюда следует, что уравнения искомой прямой имеют вид
|
|
x − x0 |
= |
|
y − y0 |
|
= |
z − z0 |
. |
|
(14.1) |
||||
|
|
|
|
|
B |
|
|
|
|||||||
|
|
A |
|
|
|
C |
|
||||||||
Задача 2. |
Составить уравнение плоскости П , проходящей через данную |
||||||||||||||
точку M 1 ( x1 , y1 , z1 ) перпендикулярно к данной прямой L |
|
||||||||||||||
|
|
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
m |
|
|
n |
|
|
|
p |
|
||||
Очевидно (см. рис. 14.2), что в качестве нормального вектора |
|||||||||||||||
плоскости |
можно взять |
|
направляющий вектор |
прямой, т.е. |
|||||||||||
R |
|
|
|
|
|
|
|
|
что уравнения искомой плоскости |
||||||
N = s = { m,n, p } . Отсюда следует, |
|||||||||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m ( x − x1 ) + n ( y − y1 ) + p ( z − z1 ) = 0 . |
(14.2) |
|||||||||||||
|
|
|
|
|
95 |
|
|
|
|
|
|
||||

M 0 (x0 , y0 , z0 )
M 1 ( x1 , y1 , z1 )
R |
= { m, n, p } |
s |
Рис. 14.2
Задача 3. Найти проекцию точки M 0 (x0 , y0 , z0 ) на плоскость
П : Ax + By + Cz + D = 0 .
Напомним, что проекцией точки M0 на плоскость называют основание перпендикуляра M1 , опущенного из этой точки на плоскость (см. рис.14.3). Очевидно, что эта проекция будет точкой пересечения плоскости П и прямой (14.1), проходящей через точку M0 перпендикулярно к этой плоскости.
N = { A, B,C }
M 0 (x0 , y0 , z0 )
M 1 ( x1 , y1 , z1 )
|
|
|
Рис. 14.3 |
|
|
|
Задача 4. Найти проекцию точки |
M 1 ( x1 , y1 , z1 ) на прямую L |
|||||
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
|
|
|
|||
|
m |
n |
p |
|||
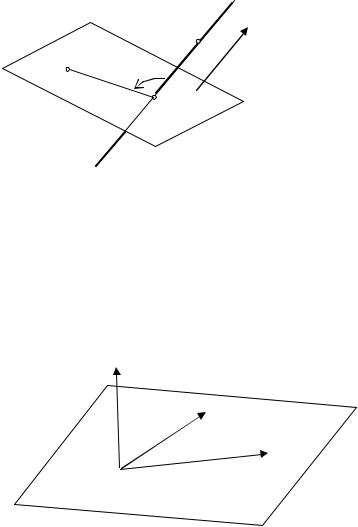
Проекцией точки M1 на прямую L в пространстве служит точка M2 пересечения прямой L и плоскости, проходящей через данную точку M1 перпендикулярно прямой L (см. рис. 14.4).
96
|
|
L |
|
M1 |
0 |
S = {m,n, p} |
|
90 |
|||
|
|
||
|
|
M2 |
Рис. 14.4
Это подсказывает и путь решения задачи: искомая проекция M2 находится как точка пересечения плоскости (14.2) и прямой L .
Задача 5. Написать уравнение плоскости, проходящей через заданную
точкуM 0 (x0 , y0 , z0 ) |
параллельно двум неколлинеарным векторам |
a = {a1, a2 , a3} и b = {b1,b2 ,b3}. |
|
2
*
0 
Рис. 14.5
Ясно, что в качестве нормального вектора к требуемой плоскости можно взять векторное произведение данных векторов, т.е.
UUR |
R R |
i |
j |
k |
|
|
|
|
|
||
N |
= a × b = |
a1 |
a2 |
a3 |
= {A, B,C}. |
|
|
b1 |
b2 |
b3 |
|
|
|
|
|
|
|
Тогда уравнение искомой плоскости имеет вид
A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0 .
Эту же задачу можно решить и другим способом. Пусть M (x, y, z) –
произвольная точка требуемой плоскости. Тогда три вектора M0M , a, b – компланарны, и уравнение плоскости получается из условия их компланарности, а именно
97

x − x0 |
y − y0 |
z − z0 |
|
= 0 . |
|
||||
a1 |
a2 |
a3 |
|
|
b1 |
b2 |
b3 |
|
|
Задача 6. Составить уравнение пучка плоскостей, проходящих через данную прямую. Пусть прямая L задана уравнениями
A1x + B1 y + C1z + D1 = 0,A2 x + B2 y + C2 z + D2 = 0.
Уравнение пучка плоскостей будет иметь вид
( A1 x + B1 y + C1 z + D1 ) + λ ( A2 x + B2 y + C2 z + D2 ) = 0 , |
(14.3) |
|
в котором λ – |
некоторый параметр. Действительно, если точка лежит на |
|
данной прямой |
L , то её координаты обращают в ноль оба уравнения, |
|
которыми задана прямая, а, значит, удовлетворяют уравнению (14.3) при любом λ. Меняя значения λ, будем получать различные плоскости, проходящие через эту прямую.
Выберем, например, из этого пучка плоскость, перпендикулярную данной плоскости П
A3 x + B3 y + C3 z + D3 = 0 .
(14.4)
Рис. 14.9
Для этого представим уравнение пучка в виде
( A1 + λA2 )x + (B1 + λB2 ) y + (C1 + λC2 )z + (D1 + λD2 ) = 0 . |
(14.5) |
98

Из перпендикулярности плоскостей (14.4) и (14.5) следует, что их нормальные векторы взаимно перпендикулярны, т.е.
( A1 + λA2 ) A3 + ( B1 + λB2 ) B3 + (C1 + λC2 ) C3 = 0 .
Отсюда находим значение λ, соответствующее искомой плоскости.
Задача 7. Написать уравнение плоскости, проходящей через заданную точку M 1 ( x1 , y1 , z1 ) и прямую.
Если прямая задана каноническими уравнениями
L : |
x − x0 |
= |
y − y0 |
= |
z − z0 |
, |
|
m |
n |
|
|
||||
|
|
|
p |
|
|||
то задача сводится к предыдущей, если в качестве вектора b взять |
|||||||
|
|
|
|
|
|
R |
= M 0 M1 . |
направляющий вектор прямой, а в качестве другого – вектор a |
|||||||
N
|
|
R |
= { m, n, p } |
M |
0 |
s |
|
|
|
||
|
M1 |
|
|
|
|
|
|
Рис. 14.6
Если же прямая задана как пересечение двух плоскостей
A1 x + B1 y + C1 z + D1 = 0
A2 x + B2 y + C2 z + D2 = 0 ,
то естественнее воспользоваться уравнением пучка плоскостей «порождённых» этой прямой
( A1 x + B1 y + C1 z + D1 ) + λ ( A2 x + B2 y + C2 z + D2 ) = 0 .
Неизвестное значение λ определяется из условия прохождения одной из плоскостей этого пучка через данную точку (см. рис. 14.7).
99
