Линейные дифференциальные уравнения высших порядков.

Рекомендуемая литература:

1. Письменный Д.Т. Конспект лекций по высшей математике. Полный курс. М. 2004.

2. Демидович б.П. Краткий курс высшей математики. М. 2004.

Учебные вопросы:

1. Линейные дифференциальные уравнения высших порядков. Структура общего

решения ЛОДУ.

2. ЛОДУ с постоянными коэффициентами.

1). Линейные дифференциальные уравнения высших порядков. Структура общего решения лоду.

Определение. Функции называются линейно независимыми на , если соотношение

(1) выполняется только при всех (т.е. если это соотношение не выполняется для отличных от нуля чисел ).

Определение. Система функций называется линейно зависимой на , если существует числа , не все равные нулю, такие, что выполняется соотношение (1).

Примеры: 1. Функции , линейно зависимы, т.к. , , .

2. Функции , , , линейно независимы.

Допустим противное – пусть они линейно зависимы. Тогда для не равных одновременно нулю, выполняется

. (2) Но, как известно, кубическое уравнение имеет только три решения . Поэтому соотношение (2) может выполняться только для трех точек, а не для . Следовательно, линейно независимы. Пусть .

Определение. Функциональный определитель вида

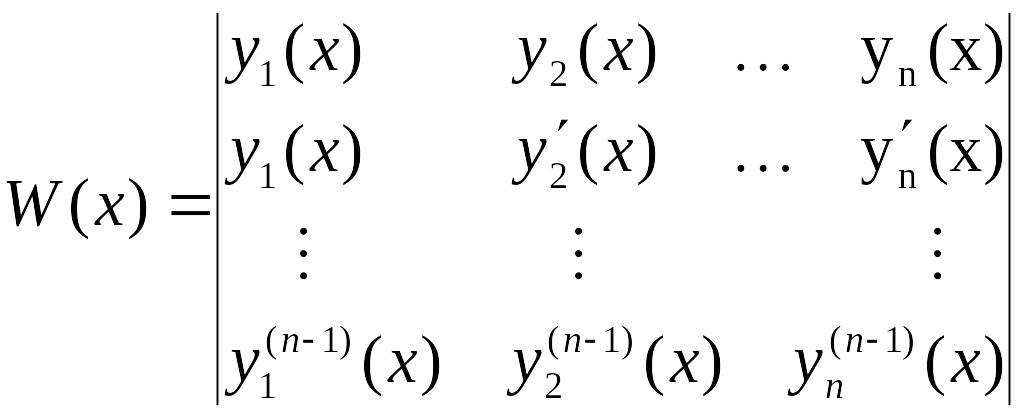
называется определителем Вронского -го порядка (вронскианом -го порядка).

Теорема (необходимое условие линейной зависимости). Если система функций линейно зависима на , то вронскиан, составленный их этих функций, равен нулю.

Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Рассмотрим однородное ЛДУ -го порядка

, (3) где . Будем искать его решение в виде

, (4) где - пока неизвестное постоянное число. Такая замена называется подстановкой Эйлера и используется потому, что при дифференцировании сохраняется ее форма. Для того, чтобы найти неизвестное число , продифференцируем раз:

- - - - - - -

и подставим в уравнение (3)

.

Внесем за скобку и сократим на него, так как

. (5) Относительно неизвестной получили алгебраическое уравнение -ой степени. Уравнение (5) называется характеристическим уравнением для ЛДУ (3). В силу основной теоремы алгебры характеристическое уравнение (5) имеет ровно корней (различных, кратных, комплексных). Поэтому рассмотрим отдельно каждый случай.

а) Корни характеристического уравнения действительные, различные . Тогда общим решением однородного уравнения (3) является

(6) Пример: Найти общее решение уравнения .

Ему соответствует характеристическое уравнение

,

имеющее корни , , . Общим решением является

.

б) Пусть у характеристического уравнения (5) корни действительные, среди них есть кратные. Пусть есть корень кратности - . Тогда этому корню соответствует решений из ФСР вида .

Пример. Найти общее решение ;

Его характеристическое уравнение ; ; ; .

Тогда .

в) Пусть некоторые корни являются комплексными. Предположим, что один некратный корень равняется . Тогда, как известно, вторым корнем будет сопряженное число . Тогда ему соответствует пара решений ФСР , .

Пример. Найти общее решение однородного ЛДУ .

Его характеристическое уравнение .

Нетрудно заметить, что один корень тогда, разделив уравнение на , получим квадратное уравнение .

Его корни , т.е. , .

Значит, общим решением исходного уравнения является функция

.

г) Пусть корни характеристического уравнения (5) комплексные кратные. Предположим, что корень есть кратности . Тогда также является корнем кратности . В этом соответствующая часть общего решения однородного ЛДУ (3) имеет вид

.

Пример. Решить уравнение .

Характеристическое уравнение или .

Корнями будут комплексные числа кратности 2: ; .

И общим решением является функция .

Сформулируем теорему, описывающую общее решение однородного ЛДУ в наиболее часто встречающемся в приложениях случае .

Теорема. Пусть и - корни характеристического уравнения для ЛДУ с постоянными коэффициентами .

Тогда возможны три случая.

1) Если и -действительные и различные - то общее решение ЛДУ есть .

2) Если , то .

3) Если , то .

Рассмотрим теперь методы нахождения частного решения неоднородного ЛДУ.

Метод Лагранжа (метод вариации произвольных постоянных)

Пусть дано неоднородное ЛДУ -го порядка

, (7) .

Предположим, что найдена или известна фундаментальная система решений однородного уравнения

. (8) Решением уравнения (7) будем искать в виде

, (9) т.е. предполагая не постоянными, а переменными и дифференцируемыми на величинами. Эти функции пока неизвестные произвольные, для нахождения их нужно иметь условий. Продифференцируем еще раз

.

Предполагая каждый раз, что сумма в квадратных скобках также равна нулю, найдем производную

.

Полагая выражение в квадратных скобах равным нулю, продифференцируем

.

Подберем так, чтобы функция (9) являясь решением уравнения (7). Подставляя функцию (9) и ее производные левую часть линейного дифференциального уравнения (7), получим

.

Так как - частные решения однородного ЛДУ, то получим последнее условие относительно . Таким образом, для нахождения неизвестных функций получили систему линейных алгебраических уравнений

(10) Решая ее методом Крамера (что можно сделать, т.к. главный определитель системы равен вронскиану , ибо - ФСР), имеем

, ,

где определители получаются из главного заменой элементов -го столбца свободными членами системы.

Метод неопределенных коэффициентов

Метод вариации можно использовать для любых линейных дифференциальных уравнений с любой непрерывной правой частью. А метод неопределенных коэффициентов можно применять только для уравнений с постоянными коэффициентами и только с правой частью определенных видов. Преимущество этого метода в том, что можно находить частное решение неоднородного уравнения, не прибегая к операции интегрирования.