1.6.7. Мінімізація логічних функцій

Метою мінімізації є зменшення вартості технічної реалізації логічних функцій незалежно від використовуваних апаратних засобів.

Логічні функції апаратно реалізуються за допомогою мікросхем, орієнтованих на виконання тих чи інших операцій. Мікросхеми загального використання здебільшого можуть реалізовувати декілька простих одиночних операцій. З цієї причини справедливо стверджувати, що чим простішою є аналітична форма запису логічної функції, тим менше використовується логічних елементів і, як результат, тим менше мікросхем необхідно для її реалізації. Складність логічних функцій визначається кількістю логічних змінних, що входять до їх складу в прямому і інверсному виді, та кількістю простих логічних операцій над ними. Будь-яка логічна функція може бути записана різними аналітичними виразами різного рівня складності. Серед них можна знайти такі, які містять мінімальну кількість логічних змінних і операцій над ними. Задача знаходження таких аналітичних виразів називається мінімізацією логічних функцій. Звідси витікає, що мінімізація логічної функції – це заміна логічної функції, що представлена у вигляді логічної суми мінтермів або логічного добутку макстермів, іншою логічною функцією з мінімальною кількістю логічних змінних та операцій над ними.

Задача мінімізації – це задача неоднозначна, і різними шляхами можна отримати різні вирази мінімізованої функції, які відрізнятимуться між собою кількістю змінних і операцій над ними.

Аналітичний спосіб мінімізації. Для зменшення складності логічних функцій здебільшого використовуються операції склеювання:

та поглинання:

Як приклад, розглянемо процедуру спрощення наступної функції:

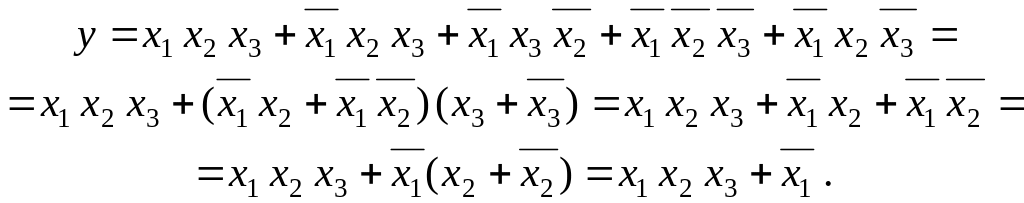
Одержана ДНФ має мінімальну складність.

Мінімізація за допомогою карт Карно (діаграм Вейча). Метод, оснований на використанні карт Карно, характеризується своєю простотою і наочністю. Зображення функції в площині координат її параметрів, подібно до алгебраїчних функцій, дозволяє наглядно встановити взаємозв’язки між її змінними і, як результат, виділити ті змінні, які є домінуючими в її визначенні.

Для пояснення методу перш за все сформулюємо основні властивості карт Карно:

• клітини карти, координати яких відрізняються лише параметрами однієї змінної, називаються сусідніми;

• сусідні клітини, значення функцій в яких або тільки істинні, або тільки хибні, можуть об’єднуватися в групи по 2^m клітин, де m – ціле число (m = 0, 1, 2, 3, …);

• при переході до аналітичної форми запису логічної функції з карти Карно вона може записуватись незмінними координатами об’єднаних груп клітин;

• у випадку неповністю визначеної функції невизначені клітини можуть бути довизначеними, виходячи з умови одержання більшої кількості об’єднаних клітин;

• одна клітина може об’єднуватись у декілька груп.

Використання карт Карно для мінімізації логічних функцій базується на наглядному використанні операції склеювання. Дійсно, дві сусідні клітки відрізняються лише однією змінною. Тому, об’єднуючи їх, ми записуємо лише незмінні координати, тобто виносимо їх за дужки. У дужках залишаються змінні координати, які об’єднуються в одну операцією склеювання. Для отримання мінімального значення функції, представленого картою Карно, окрім правил, викладених вище, необхідно користуватись загальним правилом: одиниці або нулі повинні об’єднуватись мінімальним числом найбільших контурів.

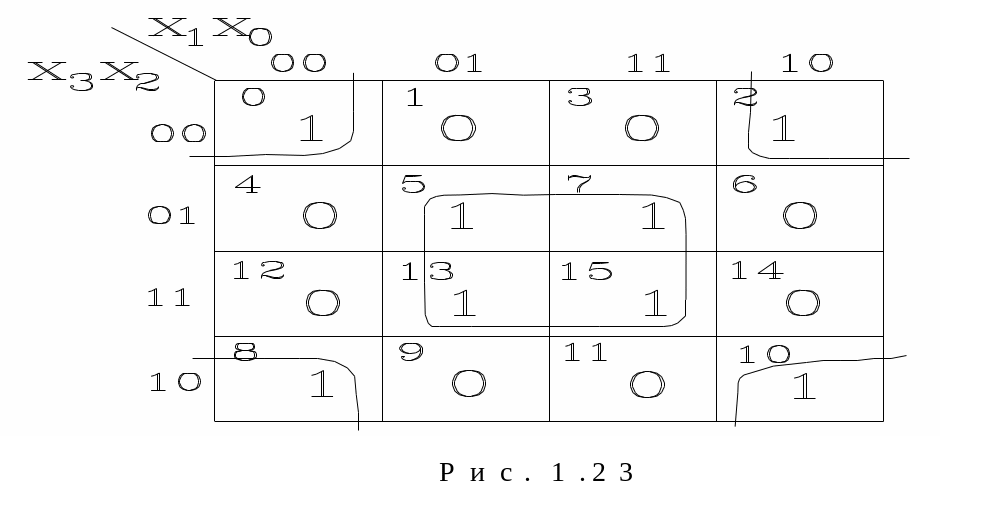
Приклад 1.33. Мінімізувати логічну функцію, що представлена у вигляді карти Карно (рис. 1.23).

Розв’язання. Об’єднуючи сусідні клітини з істинними значеннями функції (тобто клітини 0, 2, 8, 10 та клітини 5, 7, 13, 15), записуємо їх незмінні координати:

• для центральних клітин: ;

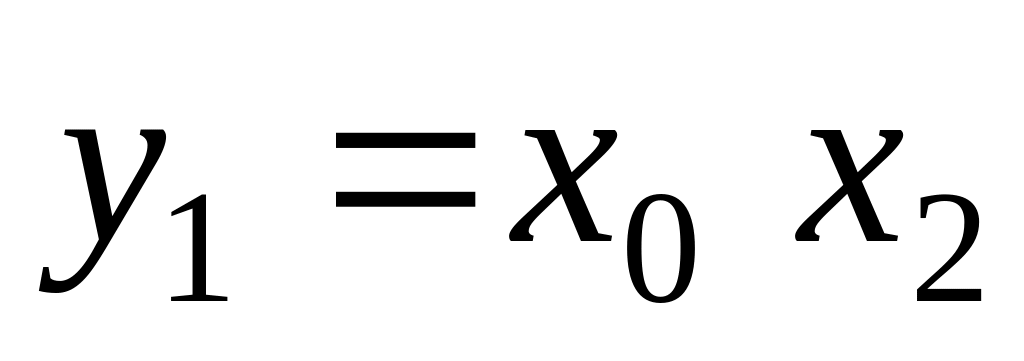• для крайніх клітин: .

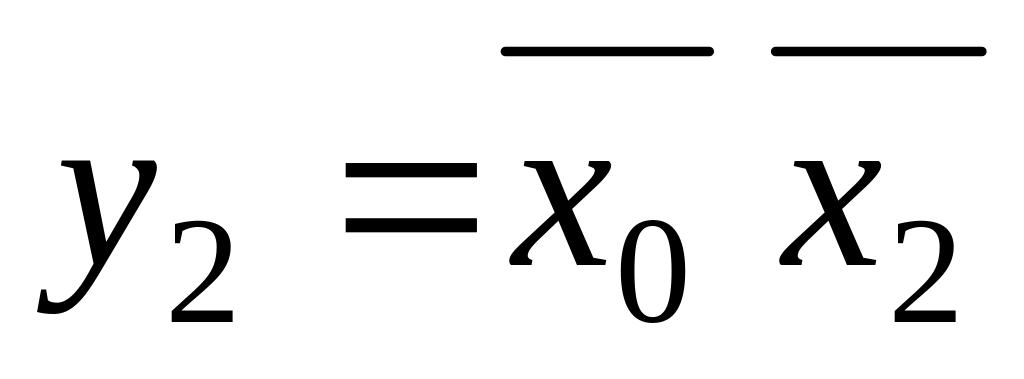Мінімізована логічна функція має вигляд:

.

Аналогічний результат буде одержаний і при об’єднанні клітин з нулями. Продемонструємо це.

Для вертикальної групи клітин (клітини 1, 3, 9, 11) знаходимо: .

Для групи горизонтальних клітин (клітини 4, 6, 12, 14): .

Мінімізована функція

операцією інверсії та теоремою де Моргана зводиться до отриманої раніше.

За допомогою карт Карно легко вирішуються задачі мінімізації функцій з кількістю змінних до шести включно. При більшій кількості змінних пошук мінімальних форм запису функцій значно ускладнюється і наочність карт Карно втрачається.

Мінімізація на основі використання кубічних комплексів. Кубічна форма зображення логічних функцій дає можливість просто і наглядно, за аналогією з використанням карт Карно, розв’язувати задачі мінімізації. Особливість такого способу мінімізації полягає в тому, що з кубічного комплексу K(у) завжди можна виділити множину кубів П(у) таких, що кожний член комплексу K₀ , тобто вершини куба (мінтерми), буде включеним по крайній мірі в один куб множини П(у). Множина кубів П(у) називається покриттям комплексу K(у), або покриттям логічної функції. Зрозуміло, що для будь-якої логічної функції існує декілька її покриттів. У той же час, кожному покриттю П(у) відповідає своя диз’юнктивна нормальна форма, отримана як сума логічних добутків відповідно виділеним кубам логічної функції.

Приклад 1.34. Для кубічного комплексу з прикладу 1.31 знайти покриття логічної функції.

Розв’язання. Кубічний комплекс логічної функції має вигляд:

K(у) = (011; 100; 101; 110; 111; -11; 11-; 1-1; 10-; 1-0; 1--).

Нульовий кубічний комплекс включає всі вершини куба, тому створює покриття функції:

П₁(у) = K₀ = (011; 100; 101; 110; 111).

Усі вершини куба включаються також в одиничний кубічний комплекс K₁ , тому він також створює покриття логічної функції:

П₂(у) = K₁ = (-11; 11-; 1-1; 10-; 1-0).

Перебираючи комбінації кубів різних рангів, можна отримати покриття логічної функції:

П₃(у) = K₂ = (011; 11-; 10-);

П₄(у) = K₃ = (-11; 1-1; 1-0);

П₅(у) = K₄ = (011; 1--);

П₆(у) = K₅ = (-11; 1--)

і т.п.

Відповідні вказаним покриттям логічні функції мають вигляд:

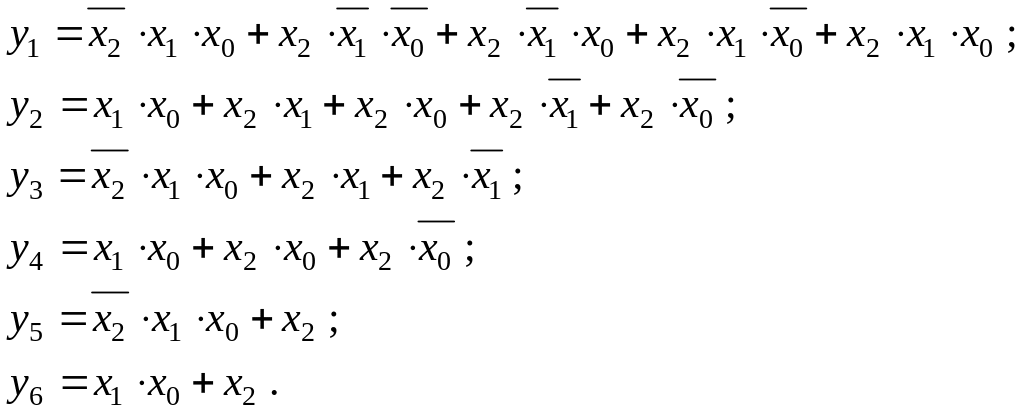
Складність отриманої таким шляхом логічної функції прийнято характеризувати поняттям “ціна покриття” (Ц_П). Ціна покриття дорівнює сумі цін всіх кубів, які складають дане покриття П(у):

Ц_П = Ц_К.

У свою чергу, ціна одного r-куба логічної функції n змінних визначається як різниця повного числа вхідних змінних і рангу відповідного куба, тобто дорівнює числу змінних у відповідній диз’юнкції:

Ц_К = n – r .

Так, для логічної функції трьох змінних ціна 0-куба дорівнює трьом, а 2-куба – одиниці.

У відповідності до сказаного, задача мінімізації логічних функцій зводиться до пошуку покриття П(у) кубічного комплексу K(у), що має мінімальну ціну.

Покриття П(у) комплексу K(у), що має мінімальну ціну, називається покриттям Квайна, а відповідна цьому покриттю логічна функція – мінімальною диз’юнктивною нормальною формою.

Мінімізація неповністю визначених логічних функцій. Серед логічних функцій зустрічаються такі, досконалі форми яких містять невизначені мінтерми (макстерми). З точки зору інженерної практики це означає, що електронна апаратура, яка розробляється, повинна бути байдужою до відповідних комбінацій логічних змінних. Зустрічаються й інші ситуації, при яких в деяких комбінаціях змінних має місце неоднозначність логічної функції. В обох випадках наявність неоднозначності використовується з метою забезпечення мінімальної форми логічної функції.

Розглянемо приклад логічної функції, що приведена на рис. 1.24.

Невизначеність її значень, що відображена у клітинах 5 та 6, може бути використана для мінімізації. Підстановка в указані клітини значень “1” дає можливість об’єднати групи клітин 1, 3, 5, 7 і 4, 5, 6, 7 та одержати мінімізовану функцію:

.

Слід зазначити, що для більш складних функцій можуть використовуватись декілька різних способів довизначення, в результаті можна отримувати мінімальні функції різної складності.

Недовизначені функції часто зустрічаються при реалізації перетворювачів кодів.

Сумісна мінімізація декількох логічних функцій. У практичних задачах цифрової електроніки дуже часто зустрічаються ситуації, коли використовується декілька різних функцій з однаковими змінними. Як приклад, розглянемо дві наступні функції:

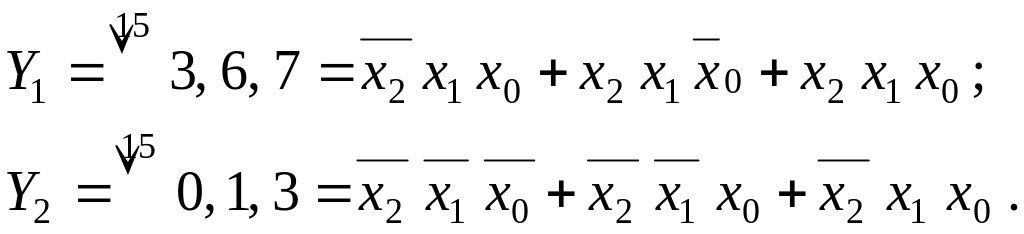
Кожну з них можна мінімізувати окремою. При такій мінімізації маємо:

Обидві функцій можуть реалізовуватись окремо. Але, порівнюючи приведені функції, бачимо, що в обох з них є загальний мінтерм. Це дає підставу окремо реалізувати загальний мінтерм, а решту мінімізовувати незалежно для кожної з функцій. У такому випадку маємо:

При побудові схеми окремо реалізуються всі терми, а потім виконується їх об’єднання через функцію АБО.

Мінімізація логічних функцій з великою кількістю змінних. Практичні комбінаційні схеми можуть мати десятки-сотні входів і виходів і описуватись сотнями-тисячами термів. У таких випадках для мінімізації широко використовується метод декомпозиції. Він полягає у наступному. Логічна функція з великою кількістю змінних – наприклад,

,

розбивається на декілька підлеглих функцій виду:

При виборі функцій f₀ , f₁ , f₂ схемотехніки використовують власний досвід, але при їх вдалому виборі апаратна реалізація мінімізованої функції може бути значно економнішою, ніж будь-які способи прямої реалізації.

Слід зазначити, що інтенсивний розвиток мікросхемотехніки, у тому числі програмованих логічних інтегральних схем (ПЛІС), постійних запам’ятовуючих пристроїв (ПЗП), а також ряду функціональних мікросхем змінив акценти в задачах мінімізації. Широке використання ПЛІС привело до розвитку методів їх програмування, які одночасно використовують і алгоритмічні засоби мінімізації кількості логічних елементів, що використовуються. Одним з таких алгоритмічних методів є метод Квайна – Мак-Класкі.

Мінімізація логічних функцій на ЕОМ за допомогою метода Квайна – Мак-Класкі. Метод використовується при необхідності мінімізації логічних функцій з великою кількістю змінних. Він, як і інші подібні методи, що мають властивість однозначності алгоритму, широко використовується і розвиваються розробниками програмних засобів для ПЛІС. Здебільшого це фірми-виробники програмованих логічних матриць (наприклад, ALTERA, XILLINХ та інші).

Алгоритм пошуку мінімальних диз’юнктивних форм зводиться до наступного:

1. Знаходиться покриття П(у) заданої функції. Для цього формується кубічний комплекс логічної функції і в кожному і-му кубічному комплексі відмічають куби (імпліканти), які не утворили (і + 1)-й кубічний комплекс. Відмічені імпліканти, які називаються простими, створюють покриття заданої логічної функції;

2. Будують таблицю покриттів матриці Квайна. Рядки вказаної таблиці відповідають простим імплікантам, а стовбці – 0-кубам (конституєнтам одиниці) логічної функції. На перетині і-го рядку та j-го стовбця ставиться мітка, якщо імпліканта і покриває конституєнту j (імпліканта і покриває конституєнту j в тому випадку, якщо вона відрізняється від неї незалежними аргументами);

3. Визначають покриття мінімальної вартості. Для цього:

   • виділяють ядро Квайна. Якщо 0-куб заданої логічної функції покривається лише однією простою імплікантою, то остання є суттєвою та входить в ядро Квайна і, відповідно, у покриття мінімальної вартості;

   • з таблиці викреслюються стовбці і рядки, які покриті імплікантами ядра Квайна. Якщо в отриманій після викреслювання таблиці містяться прості імпліканти, вони також включаються в ядро Квайна з послідуючим викресленням відповідних рядків і стовбців;

   • стискається таблиця по стовбцях, для чого з неї викреслюються стовбці, які повністю включаються в будь-який з решти стовбців;

   • стискається таблиця по рядках, для чого з неї викреслюються рядки, які повністю включаються в будь-яку з решти рядків.

Послідовно стискаючи таблицю по рядках і стовбцях, отримують циклічну таблицю, імпліканти якої повинні входити в покриття логічної функції мінімальної вартості.