Лекция 3.6. Задачи, приводящие к определенному интегралу. Общие идеи интегрального исчисления. Различные типы Определенных интегралов. Теорема существования, свойства

3.6.1. Задачи, приводящие к понятию общего интеграла

При решении целого ряда технических и физических задач приходится суммировать бесконечно большое число бесконечно малых величин. Вычисление этих сумм привело к одному из центральных понятий математики, к понятию определенного интеграла. Рассмотрим одну из таких задач.

Задача. Найти массу пяти неоднородных тел различной формы с известными размерами: прямолинейного тонкого стержня, тонкого изогнутого стержня (обозначим его буквой L) длиной ℓ лин. ед., тонкой пластины D с площадью S кв.ед., тонкой изогнутой пластины q размером σ кв.ед., и наконец некоторого объемного тела W с объемом V куб.ед.

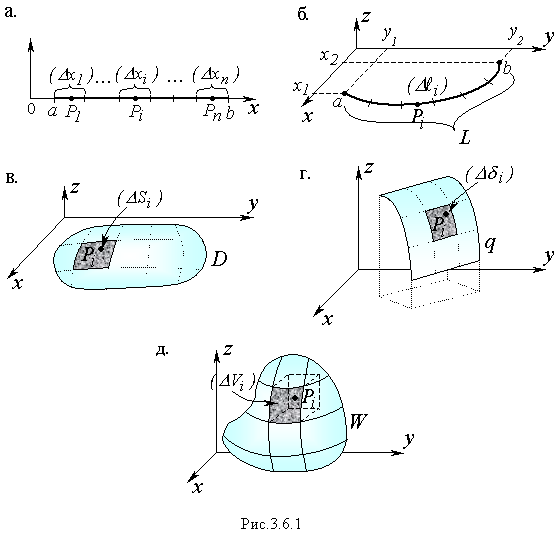
Чтобы решить данную задачу, расположим все тела определенным образом в декартовой системе координат. Прямолинейный тонкий стержень примем за отрезок прямой и поместим его на ось Ох между точками х = α и х = b, тогда длина его будет равна (b – α) (рисунок 3.6.1а).

Изогнутый стержень, длиной ℓ, можно считать частью кривой линии L, расположенной в плоскости xОy между точками α(x_1,y₁) и b(x_2,y₂), (рисунок 3.6.1б).

Тонкую пластину D площадью S кв.ед., примем за плоскую область D на координатной плоскости xОy, (рисунок 3.6.1в).

Тонкую изогнутую пластину, размером σ кв.ед., будем считать частью некоторой поверхности q в декартовой системе координат (рисунок 3.6.1 г), и наконец, тело произвольной формы, с объемом V куб.ед., – это некоторая область W, расположенная определенным образом в выбранной системе отсчета (рисунок 3.6.1.д).

Предположим, что при таком расположении тел значения плотности массы ρ во всех точках каждого из них известно, т.е. известен закон распределения плотности массы, или дана функция:

ρ = ρ(Р)

где Р – точки, принадлежащие телам.

У прямого и кривого стержней этой функцией будем считать линейную плотность, которую находят по формулам:

Для полоской и изогнутой пластин будем предполагать, что плотность массы поверхностная, т.е. равна пределам:

Для объемного тела W ее находят, как обычно:

Известно, что масса однородных тел, у которых ρ(Р) = const, равна произведению плотности массы на размер тела. Если бы тела были однородными, то их массу мы могли бы найти по формулам:

Но так как тела не однородные, поступим так же, как в первых двух задачах.

Разобьем каждое тело на n малых частей произвольным образом. Прямой стержень – на частичные интервалы: , длину которых мы обозначим без круглых скобок:

Изогнутый стержень L – на частичные линии с длинами , i = 1,2,…n.

Плоскую и изогнутую пластины D и q – на элементарные части и площадью и соответственно, i = 1,2,…n; и наконец, тело W – на элементарные части с объемами .

На прямом стержне (b – α) внутри каждого частичного интервала произвольным образом возьмем точку (рисунок 3.6.1.а). В выбранных точках найдем значение плотности массы:

Аналогичную операцию проделаем для всех остальных тел (рисунок 3.6.1). Если плотность массы ρ(Р) – непрерывная функция и все тела разбиты на достаточно малые кусочки, то в пределах одной элементарной части всех тел плотность массы будет меняться незначительно и ее приближенно можно считать постоянной, равной значению в выбранной точке.

Поэтому массу i-ой части каждого тела можно найти приближенно, как произведение плотности ρ(Р_i) на размеры части:

Для прямого стержня [α,b]:

Для изогнутого стержня L:

Для плоской пластины D:

Для изогнутой пластины q:

Для тела W:

Масса каждого из пяти тел будет равна сумме масс элементарных частей, на которые они были разбиты. Заменяя элементарные массы их приближенными значениями, получим:

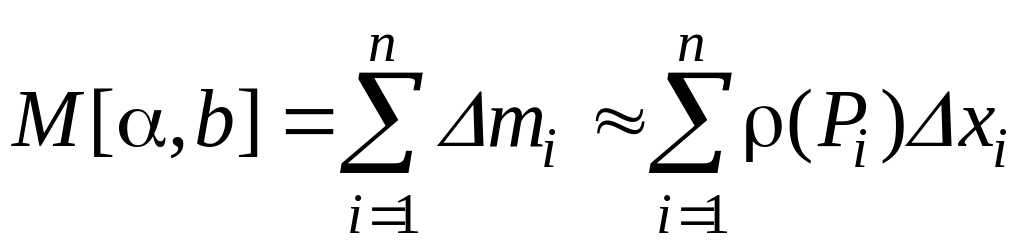
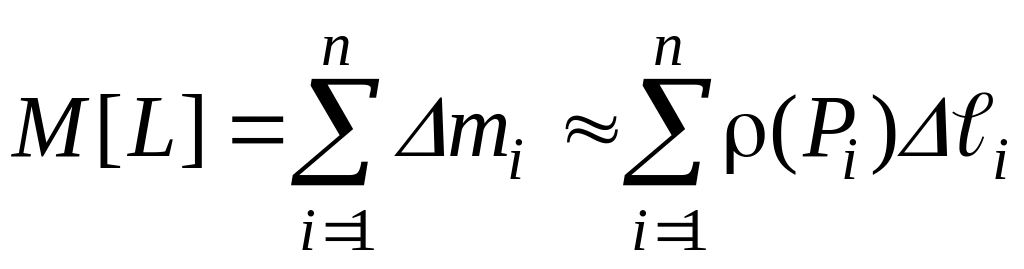
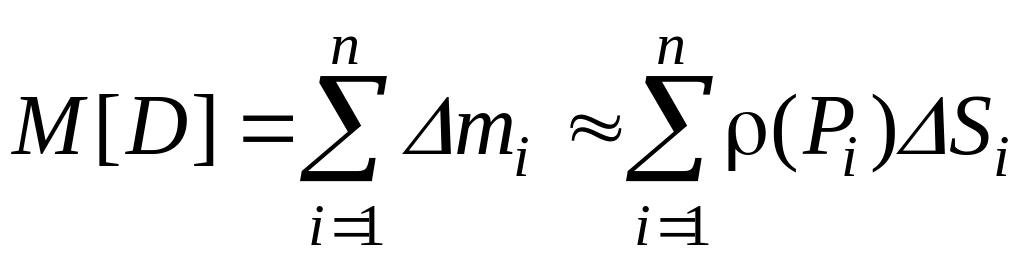
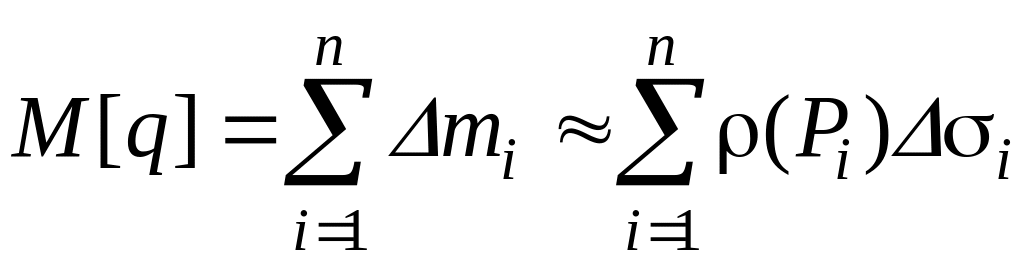
Назовем диаметром элементарной части максимальное из расстояний между двумя ее точками. Очевидно, что массы тел, вычисленные с помощью найденных сумм, будут тем точнее, чем мельче их разбиение на отдельные части. При n → ∞, или при стремлении к нулю наибольшего из диаметров элементарных кусочков, т.е. при переходе к пределу, мы получим точное значение для масс всех тел:

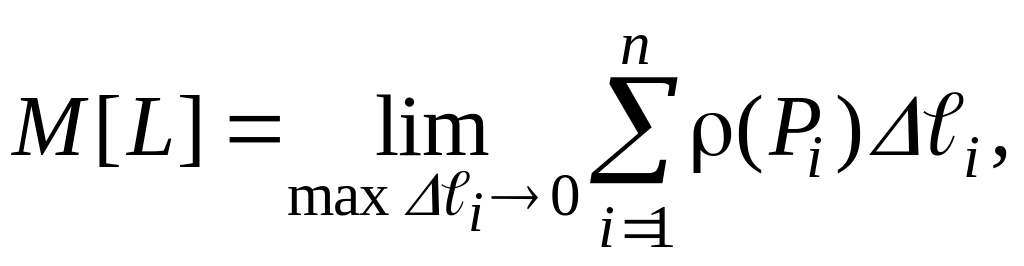
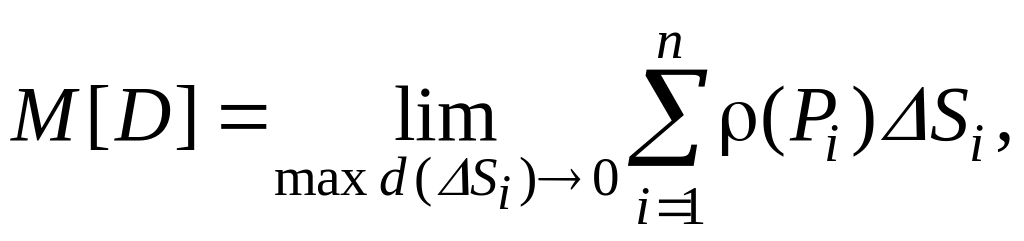
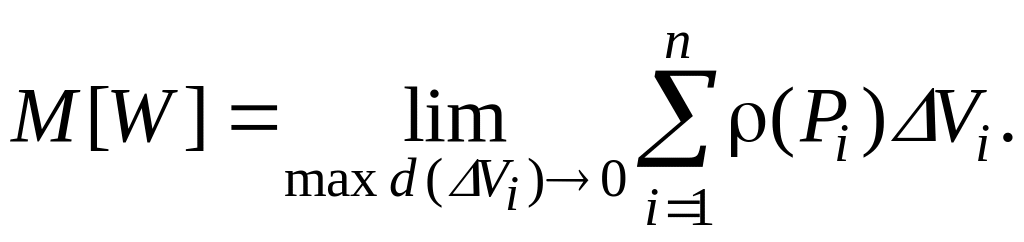
Из приведенного примера следует, что когда распределение значений различных физических величин неравномерное, решение довольно широкого класса задач сводится к одинаковым математическим операциям, а именно к составлению суммы одного и того же вида и вычислению ее предела.