Часть III Динамика Классификация сил. Динамика материальной точки.

Силу оценивают по движению, которое она вызывает или стремится вызвать в рассматриваемой системе координат, которую мы условились считать неподвижной (инерциальной).

а) Потенциальные силы – силы, которые могут быть выражены через некоторую скалярную функцию от положения точки, называемой потенциальной энергией.

Работа на конечном перещении точки из положения в положение равна определенному интегралу

,

т.е. не зависит от формы траектории, является только функцией начального и конечного положения.

б) Гироскопические силы - линейно зависят от скорости точки и всегда направлены перпендикулярно этой скорости, работа гироскопических сил, очевидно, всегда равна нулю (примеры – сила инерции Кориолиса, магнитная часть силы Лоренца).

в) Диссипативные силы - направлены всегда противоположно скорости тела относительно среды, вызывающей торможение.

,

где k – положительная скалярная функция, которая может зависеть от положения и скорости тела. Всегда A(F^d) < 0 – работа диссипативных сил (сил сопротивления) всегда отрицательна.

Вся динамика построена на предположении о том, что в природе существуют инерциальные системы отсчета (ИСО) (неподвижные или движущиеся равномерно и прямолинейно).

Законы Ньютона

1. Каждое тело пребывает в состоянии покоя или равномерного прямолинейного движения до тех пор, пока действующие на тело силы не заставят его изменить движение (причиной изменения движения является сила).

2. Ускорение пропорционально приложеной силе и направлено по прямой, по которой действует сила: (количественная мера действия силы)

3. Силы взаимодействия двух материальных точек равны по величине и противоположны по направлению (сила всегда имеет материальный источник, который испытывает обратное действие объекта, к которому приложена сила)

Динамика является наукой об ускоряющих силах и о тех движениях, которые эти ускоряющие силы могут вызвать.

2-й закон Ньютона

Сила может быть функцией . Эти три дифференциальных уравнения 2^го порядка имеют общее решение, зависящее от шести произвольных постоянных, определяемых из начальных условий.

Аксиома о суперпозиции сил.

При одновременном действии на материальную точку нескольких сил ускорение точки относительно ИСО от действия каждой отдельной силы не зависит от наличия других приложенных к точке сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.

Между силами нет взаимного влияния друг на друга в создании ускорения точки:

;

;

;

Все это справедливо для небольших скоростей.

Размерностью силы является в системе СИ ньютон ([F]=н). Сила в 1н равна силе, сообщающей телу массой 1 кг ускорение, равное 1 м/с².

Дифференциальные уравнения движения материальной точки. Две основные задачи динамики точки.

- равнодействующая,

Декартова система координат:

Естественная система координат:

Второе уравнение можно преобразовать:

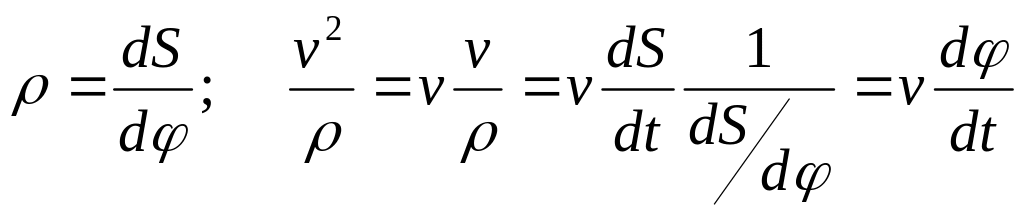
Получаем для естественной системы координат:

Первая (прямая) задача динамики точки: зная массу точки и ее закон движения, можно

найти действующую на точку силу.

Зная проекции силы на координатные оси, легко определить модуль силы и косинусы углов силы с осями координат.

Пример: x=aCoskt; y=bSinkt, точка массы m.

- эллипс с полуосями a, b

F_x= -mk²aCoskt; F_y= -mk²bSinkt или F_x= -mk²x; F_y= -mk²y

(r-радиус-вектор точки)

Косинусы углов силы F с осями координат:

Отсюда можно заключить, что сила F имеет направление, противоположное вектору r.

Окончательно

Вторая (обратная) задача динамики точки: по заданой массе и действующей на точку

силе необходимо определить движение (закон движения) точки,

В некоторых случаях силы могут зависеть и от ускорений.

Для нахождения уравнений движения точки в декартовых координатах необходимо проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка. Решение системы содержит шесть произвольных постоянных С₁,C₂,C₃,C₄,C₅,C₆.

Каждая из координат x,y,z движущейся точки после интегрирования системы зависит от времени и всех шести постоянных

x=f₁(t, С₁,C₂,C₃,C₄,C₅,C₆); y=f₂(t, С₁,C₂,C₃,C₄,C₅,C₆); z=f₃(t, С₁,C₂,C₃,C₄,C₅,C₆)

Если продифференцировать решения, то для скоростей будем иметь:

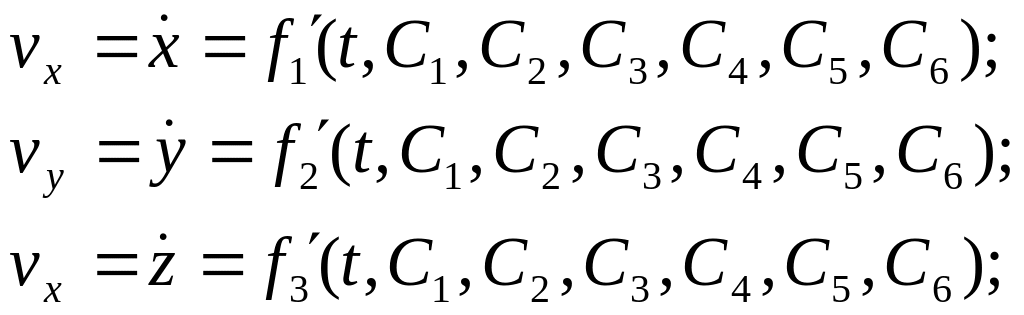
Таким образом, действующая сила однозначно определяет только ускорение точки и задает целый класс движений, траектории которых и скорости зависят от начального положения и скорости.

Для определения конкретного вида движения необходимо задать начальные условия:

в некоторый момент времени t₀ (t=0).

Используя эти условия получаем шесть уравнений для определения произвольных постоянных:

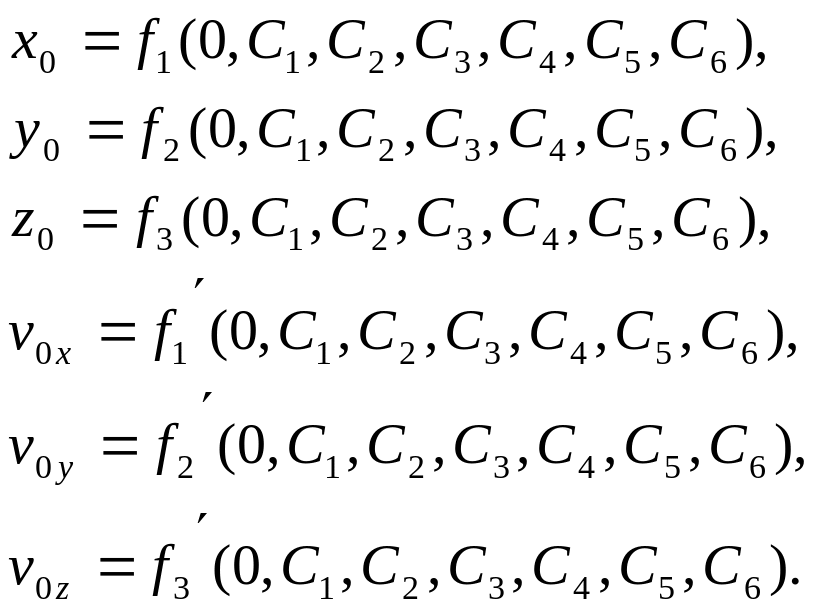
Начальные условия определяют единственное решение системы дифференциальных уравнений.

При движении точки в плоскости Oxy имеется два дифференциальных уравнения движения. В решения этих уравнений входят четыре произвольные постоянные, которые определяются из начальных условий:

Для прямолинейного движения имеется только одно уравнение и в его решение входят две произвольные постоянные, определяемые из начальных условий:

Задача интегрирования системы дифференциальных уравнений в общем случае является довольно трудной. Даже для одномерного случая решение удается выразить точно в квадратурах лишь при определенной зависимости силы от t, x и v.