5.6. Построение кривых переходного процесса

Теоретически кривая переходного процесса получается при решении дифференциального уравнения операторным методом, путем отыскания оригинала выходного сигнала при заданном типовом воздействии. График решения дифференциального уравнения и является кривой переходного процесса.

В курсе рассматриваются следующие методы построения кривой переходного процесса:

- метод трапецеидальных вещественных частотных характеристик (самостоятельно);

- на основе разностных уравнений.

5.6.1. Разностные уравнения

Построение кривой переходного процесса на основе разностных уравнений предполагает дискретизацию непрерывных (аналоговых) уравнений.

Процесс дискретизации можно представить в виде работы следующего элемента (ключа) (рис. 5.9), где t – шаг дискретизации.

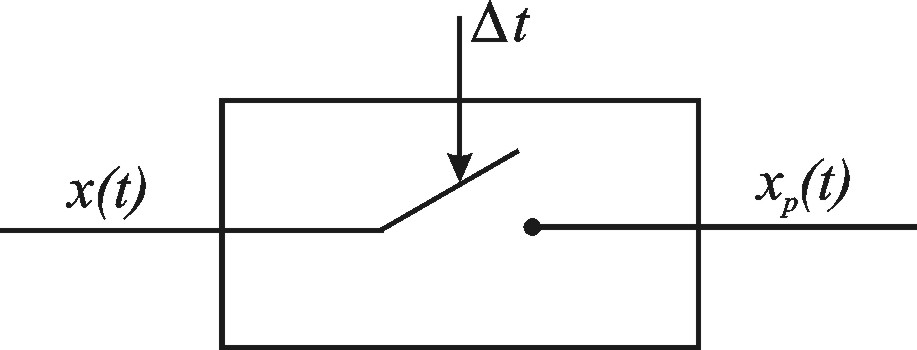
Рис. 5.9. Схема дискретизации переменной

Пусть x(t) – входной сигнал элемента представляет собой решение дифференциального или интегро-дифференциального уравнения (рис. 5.10а). На выходе ключа имеем сигнал x_p(t), представленный на рис. 5.10б, т.е. последовательность импульсов длительностью h, где h – время замыкания ключа. Если h<<t, то временем замыкания ключа можно пренебречь, что показано на рис. 5.10в.

Математически этот сигнал записывается в виде:

. (5.16)

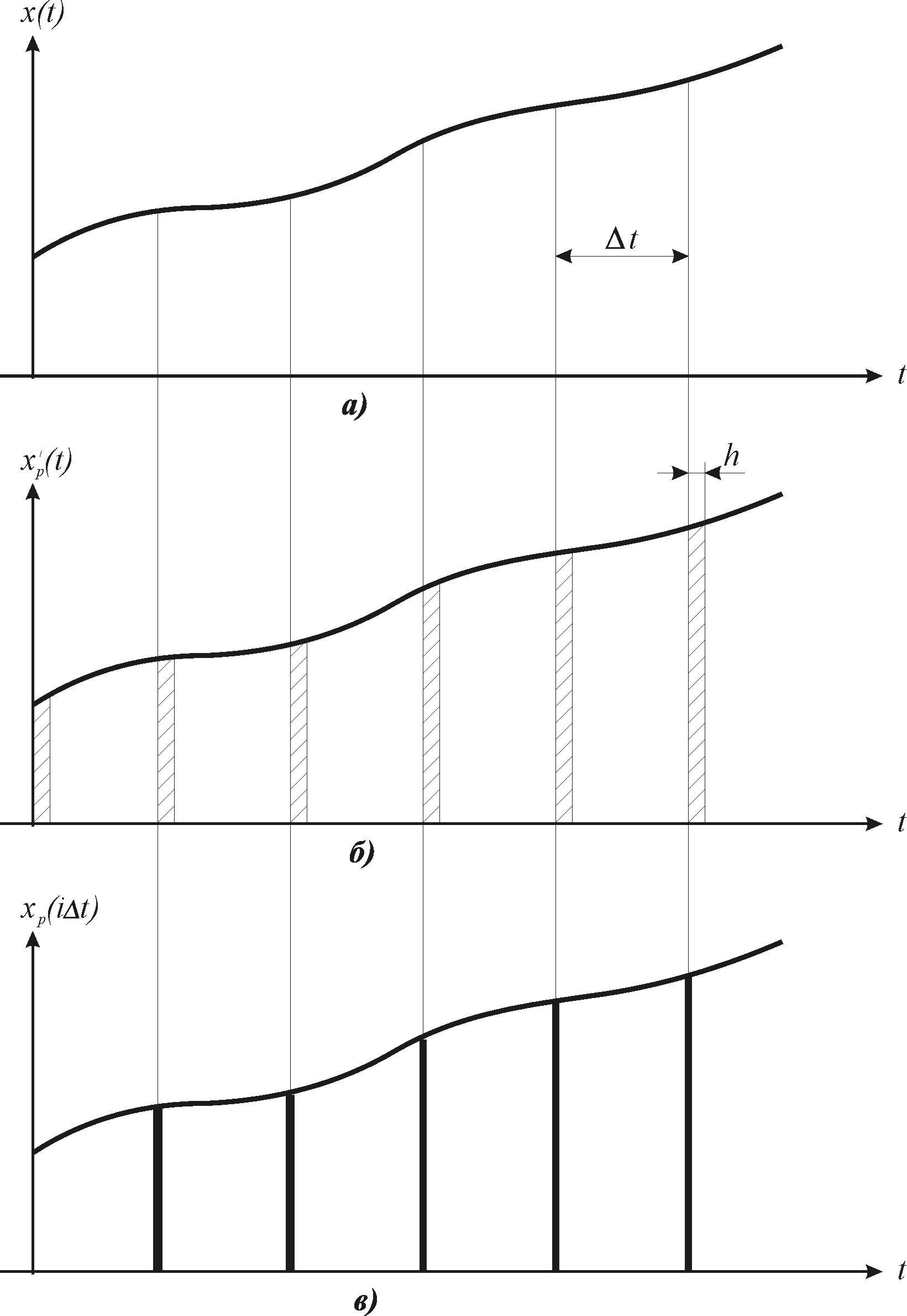
Рис. 5.10. Процесс дискретизации сигнала

и называется такой сигнал дискретным или решетчатым. Время t_i=it называется дискретным временем. Если шаг дискретизации постоянный (t=const), то вместо дискретного времени t_i=it используют аналог дискретного времени i, представляющий собой целое число. Тогда дискретный сигнал записывается в виде x(i), т.е.

x(i)= x_р(it). (5.17)

Для получения дискретного сигнала x(i) на основе непрерывного x(t), представляющего собой решение дифференциального или интегро-дифференциального уравнения, достаточно последний дискретизировать с шагом t в соответствии с выражением (5.17). Например:

, то .

Дискретный сигнал x(i) можно получить и путем дискретизации непрерывных (дифференциальных или интегро-дифференциальных) уравнений, т.е. путем перехода к разностным уравнениям. Для получения разностного уравнения достаточно любую дискретную функцию, зависящую от другой дискретной функции представить в рекуррентной форме.

Линейное разностное уравнение n-го порядка записывается в виде:

, (5.18)

где i – аналог дискретного времени; a₀, a₁,…,a_n, b₀, b₁,…,b_m – коэффициенты разностного уравнения.

Выразив y(i) из уравнения (5.18), получим рекуррентную формулу вида:

(5.19)

где

5.6.2. Получение разностного уравнения на основе интегрального уравнения

Пусть интегральное уравнение имеет вид:

. (5.20)

По определению интеграл представляет собой площадь криволинейной трапеции (рис. 5.11). При использовании метода прямоугольников для численного интегрирования получаем следующую сумму

, (5.21)

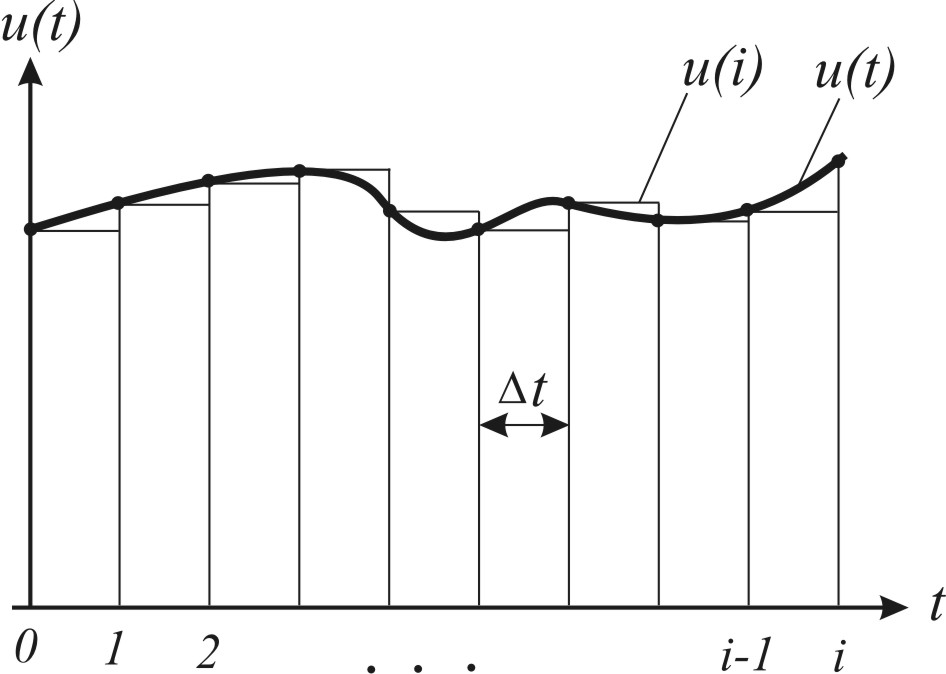
Рис.5.11. Дискретизация интегрального уравнения методом прямоугольников

т.е. площадь криволинейной трапеции заменяется приближенно суммарной площадью прямоугольников с основанием t и высотой u(i). Тогда для i-1-го шага, т.е. предыдущего отчета имеем:

. (5.22)

Вычтя выражение (5.22) из (5.21) получим уравнение вида:

,

т.е. разностное уравнение вида:

, (5.23)

где а₁=-1; b₁=t /T.

Отсюда

, (5.24)

где ₁=b₁.