
- •Содержание
- •Введение
- •Краткий теоретический курс отс
- •1. Предмет и метод
- •2. Статистическое наблюдение
- •3. Статистические показатели
- •Виды обобщающих показателей
- •4. Статическая сводка, группировка
- •5. Статистические графики и таблицы Статистические графики
- •Статистические таблицы
- •Классификация статистических таблиц
- •Основные правила составления и оформления таблиц
- •6. Средние величины и показатели вариации Средние величины
- •Основные свойства средней арифметической
- •Средняя геометрическая:
- •Показатели вариации
- •Основные свойства дисперсии
- •Показатели вариации альтернативного признака
- •Показатели вариации для сгруппированных признаков
- •Моменты распределения
- •Показатели асимметрии и эксцесса
- •7. Статистический анализ динамических рядов Показатели динамического ряда
- •1. Если динамический ряд обозначить как , то:
- •1. Если динамический ряд обозначить как , то:
- •Методы выявления тренда в динамических рядах.
- •Выделение тренда динамического ряда
- •Аналитическое выравнивание по прямой
- •Аналитическое выравнивание по параболе второго порядка
- •Статистический анализ случайной величины.
- •Анализ сезонных колебаний ряда динамик
- •Метод абсолютных и относительных разностей.
- •Расчет индексов сезонности.
- •Если тренд отсутствует, то
- •8. Статистические индексы
- •9. Выборочное наблюдение
- •Методы и способы отбора, обеспечивающие репрезентативность выборки
- •Ошибки выборочного наблюдения
- •Определение средней ошибки выборочного наблюдения.
- •Определение предельной ошибки выборочного наблюдения.
- •Определение необходимой численности выборки
- •Способы распространения характеристик выборки на генеральную совокупность
- •Распределение вероятности в малых выборках в зависимости от значения коэффициента доверия и численности выборки
- •10. Корреляционно-регрессионный анализ
- •Общие положения по выполнения контрольной работы
- •Правила оформления контрольной работы
- •Правила оформления иллюстраций, графиков, диаграмм
- •Титульный лист
- •Выбор варианта контрольной работы
- •Контрольные вопросы Предмет и метод статистики
- •Статистическое наблюдение
- •Статистические показатели
- •Статистическая сводка, группировка
- •Статистические графики, таблицы
- •Средние величины и показатели вариации
- •Статистический анализ динамических рядов
- •Статистические индексы
- •Выборочное наблюдение
- •Корреляционно-регрессионный анализ
- •Задачи Статистические показатели
- •Средние величины и показатели вариации
- •Статистический анализ динамических рядов
- •Статистические индексы
- •Выборочное наблюдение
- •Корреляционно-регрессионный анализ
- •Варианты контрольных заданий
- •Вопросы к тестам
- •Коэффициент эластичности показывает;
- •Коэффициент регрессии рассчитывается как:
- •Коэффициент эластичности рассчитывается как:
- •Ответы на вопросы к тестам
- •Приложения
- •(Наименование дисциплины)
- •(Обозначение документа)
- •Приложение 2
- •Греческий алфавит
- •Список литературы в основу работы положены следующие учебные и справочные пособия:
Основные свойства средней арифметической
Средняя арифметическая постоянной величины равна этой постоянной.
Если каждую варианту
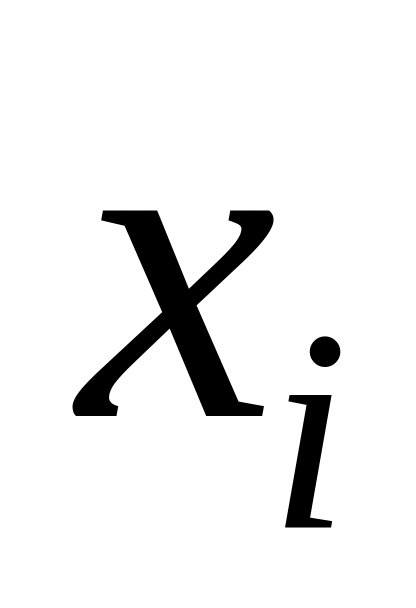 увеличить или уменьшить на одно и то
же постоянное число, то новая средняя
увеличится или уменьшится на это же
число.
увеличить или уменьшить на одно и то
же постоянное число, то новая средняя
увеличится или уменьшится на это же
число.Если каждую варианту умножить или разделить на одно и то же постоянное число, то новая средняя увеличится или уменьшится во столько же раз.
Сумма всех отклонений вариантов от средней (как простой, так и взвешенной) всегда равна нулю:
![]() и
и
![]() ,
(6.5)
,
(6.5)
Сумма всех квадратов отклонений вариантов от средней (как простой так и взвешенной) всегда меньше суммы квадратов отклонений от любой другой произвольной величины:
![]() ,
(6.6)
,
(6.6)
Если все частоты разделить (умножить) на одно и то же постоянное число, средняя от этого не изменится.
Средняя многочлена равна многочлену средних:
![]() .
(6.7)
.
(6.7)
Средняя
гармоническая
применяется при обобщении обратных
![]() значениях изучаемого явления.
значениях изучаемого явления.
Прямые значения
признака
![]()
такие значения, которые увеличиваются
при увеличении определяющего показателя
и характеризуемых ими явлений и
уменьшаются при уменьшении.
такие значения, которые увеличиваются
при увеличении определяющего показателя
и характеризуемых ими явлений и
уменьшаются при уменьшении.
Обратные
значения признака
![]()
такие значения, которые увеличиваются
при уменьшении определяющего показателя
и характеризуемых ими явлений и
уменьшаются при увеличении.
такие значения, которые увеличиваются
при уменьшении определяющего показателя
и характеризуемых ими явлений и
уменьшаются при увеличении.
Средняя гармоническая простая:
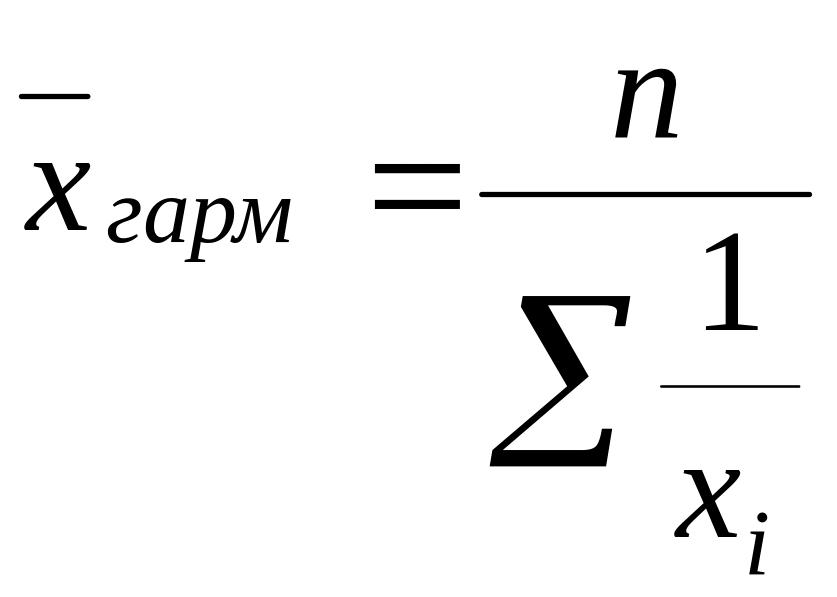 ,
(6.8)
,
(6.8)
Средняя гармоническая взвешенная:
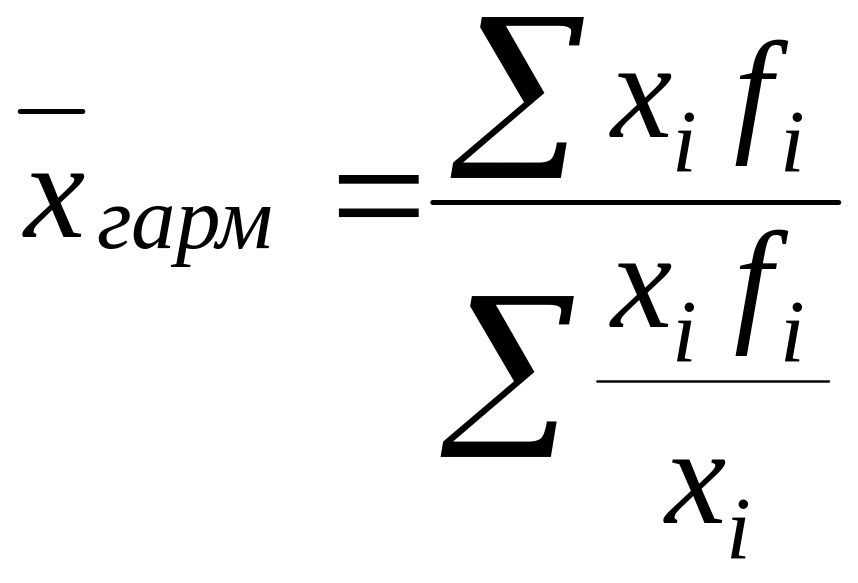 ,
(6.9)
,
(6.9)
Средняя квадратическая простая:
![]() ,
(6.10)
,
(6.10)
Средняя квадратическая взвешенная:
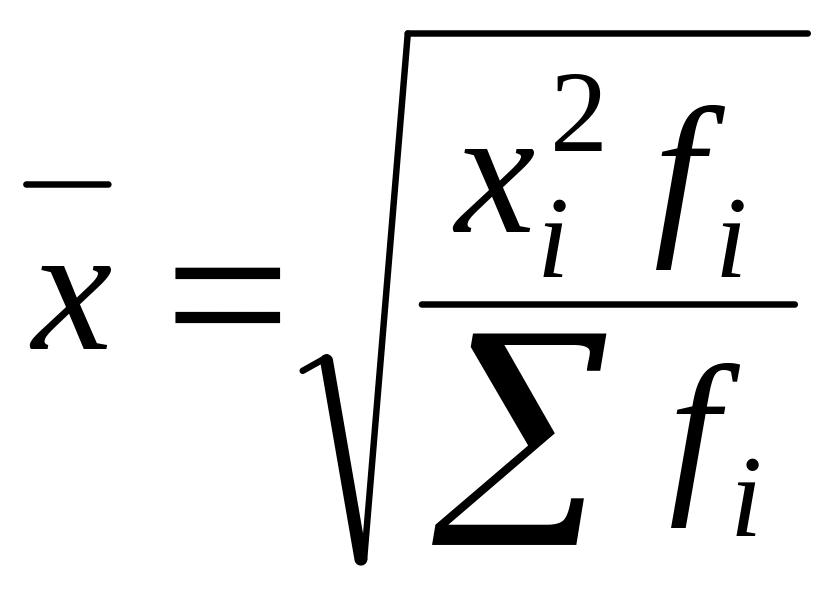 ,
(6.11)
,
(6.11)
Средняя кубическая простая:
![]() ,
(6.12)
,
(6.12)
Средняя квадратическая взвешенная:
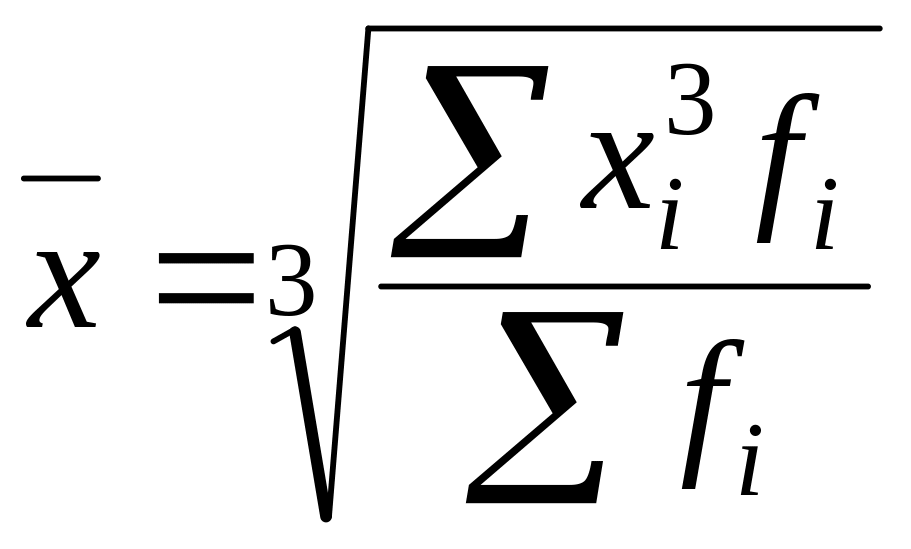 .
(6.13)
.
(6.13)
Средняя геометрическая:
![]() ,
,
![]() ,
(6.14)
,
(6.14)
где – число значений признака;
![]() – знак перемножения;
– знак перемножения;
![]() – варианта признака.
– варианта признака.
Мода – наиболее часто встречающееся значение признака в исследуемой совокупности.
Медианой называется такое значение признака, которое стоит в середине ряда вариант расположенных по порядку возрастания или убывания (ранжированный ряд). Медиана делит ранжированный ряд пополам, в результате чего у половины единиц совокупности значение признака меньше медианы, а у половины больше медианы.
Мода в дискретном вариационном ряду определяется частотой появления той или иной величины варианты, варианта с наибольшей частотой – мода.
Мода в вариационном интервальном ряду рассчитывается по формуле:
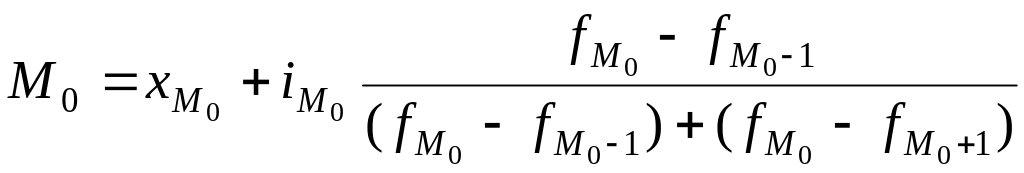 ,
(6.15)
,
(6.15)
где
![]()
минимальная граница модального интервала;
минимальная граница модального интервала;
![]() величина
модального интервала;
величина
модального интервала;
![]() частота интервала
предшествующая модальному интервалу;
частота интервала
предшествующая модальному интервалу;
![]() частота следующего
за модальным интервалом;
частота следующего
за модальным интервалом;
![]()
частота модального
интервала.
частота модального
интервала.
Модальный интервал это интервал, содержащий моду (имеющий наибольшую частоту).
Медиана в дискретном вариационном ряду рассчитывается в зависимости от того, четное или нечетное количество элементов содержит ряд.
При нечетном
количестве единиц
определяется
номер варианты![]() ,
которому соответствует медиана:
,
которому соответствует медиана:
![]() ,
(6.16)
,
(6.16)
При четном количестве единиц:
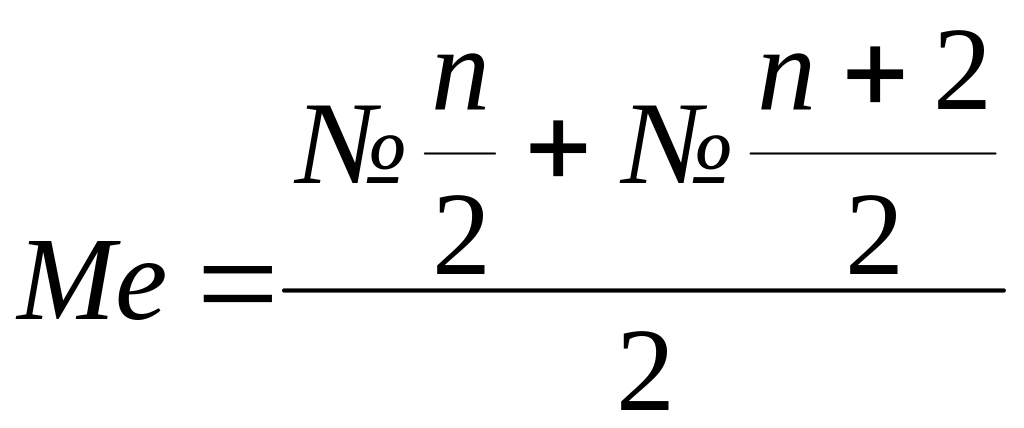 ,
(6.17)
,
(6.17)
Медиана в интервальном вариационном ряду рассчитывается по формуле:
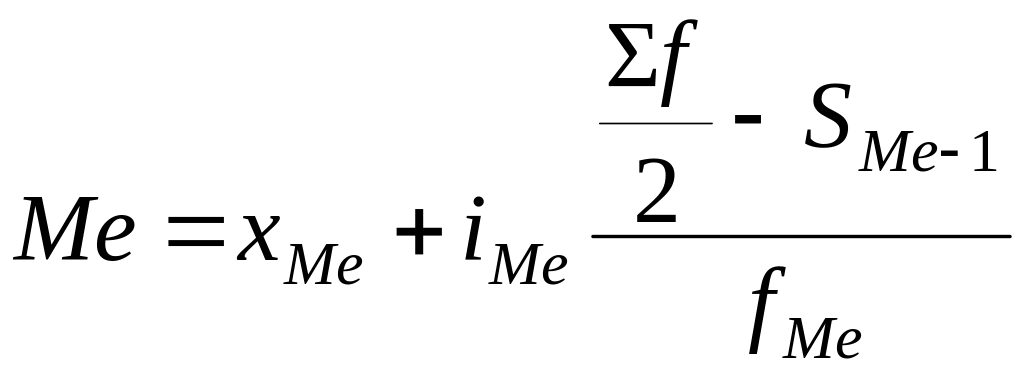 ,
(6.18)
,
(6.18)
где
![]()
начальное значение медианного интервала;
начальное значение медианного интервала;
![]() величина
медианного интервала;
величина
медианного интервала;
![]()
сумма частот ряда;
сумма частот ряда;
![]() сумма накопленных
частот, всех интервалов, предшествующих
медианному;
сумма накопленных
частот, всех интервалов, предшествующих
медианному;
![]() – частота медианного
интервала.
– частота медианного
интервала.
Медианный интервал это интервал, кумулятивная (накопленная) частота которого равна или превышает половину суммы частот.
Квартиль
делит ряд
на четыре одинаковые части. Второй
квартиль равен медиане. Расчет первого
![]() и третьего
и третьего
![]() осуществляется по формулам:
осуществляется по формулам:
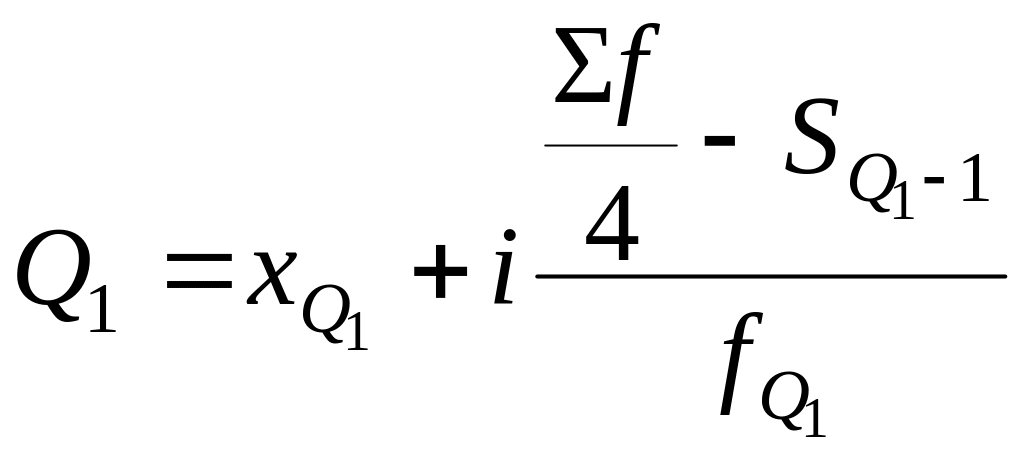 ,
(6.19)
,
(6.19)
Вместо медианного интервала при расчете берется интервал, в котором находится варианта, отсекающая ¼ численности частот:
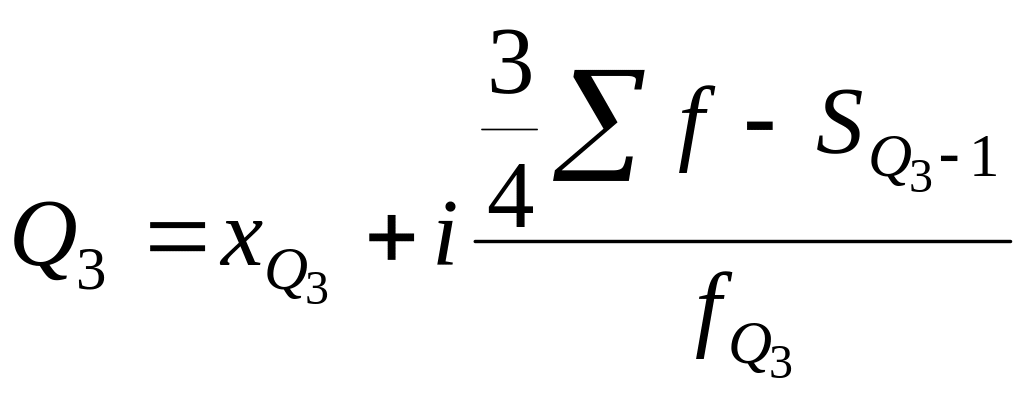 ,
(6.20)
,
(6.20)
Вместо медианного
интервала при расчете
![]() берется интервал, в котором находится
варианта, отсекающая ¾ численности
частот.
берется интервал, в котором находится
варианта, отсекающая ¾ численности
частот.
Дециль делит ранжированный ряд на 10 равных частей.
