
6.4. Вихревой характер магнитного поля. Теорема Гаусса для магнитного поля
Теоретический расчет индукции магнитного поля прямолинейного провода с током показал, что линии индукции магнитного поля замкнуты сами на себя. Теория электромагнетизма и экспериментальные данные указывают, что замкнутость линий индукции является общим свойством любого магнитного поля. Заметим, что линии напряженности электростатического поля начинаются на положительных электрических зарядах, а заканчиваются на отрицательных зарядах
Для электростатического поля закон Кулона в дифференциальной форме записывается как
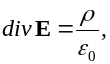 (1.60)
(1.60)
где
величина
![]() характеризует мощность источников поля
характеризует мощность источников поля
![]() в каждой точке, которая пропорциональна
объемной плотности электрического
заряда.
в каждой точке, которая пропорциональна
объемной плотности электрического
заряда.
В силу отсутствия магнитных зарядов мощность источников магнитного поля равна нулю, и вместо (1.60) для магнитного поля получим
![]() (6.10)
(6.10)
Понятие магнитного потока введем по аналогии с понятием потока линий напряженности электрического поля. Магнитный поток через поверхность с единичной нормалью выражается как поверхностный интеграл от индукции магнитного поля:
![]() (6.11)
(6.11)
Из (6.11) следует другое название для магнитной индукции - плотность магнитного потока, как магнитный поток в расчете на единицу площади поверхности.
Пусть теперь поверхность - замкнутая, для которой нормаль выбрана внешней. Для магнитного поля применим формулу Гаусса-Остроградского, которая связывает мощность источников поля с потоком порождаемого ими векторного поля:
![]() (6.12)
(6.12)
С учетом (6.10) вместо (6.12) получаем, что магнитный поток через любую замкнутую поверхность равен нулю:
![]() (6.13)
(6.13)
Формула (6.13) выражает теорему Гаусса для магнитного поля.
6.5. Формула полного тока
Обратимся
к формуле (6.6) и рис. 6.5, которые отражают
результаты расчета магнитного поля
прямолинейного провода с постоянным
током. Выразим циркуляцию индукции
магнитного поля
![]() вдоль контура, совпадающего с выделенной
линией индукции магнитного поля
(окружностью на рис. 6.5). Обозначим
- радиус окружности. Так как величина
остается постоянной вдоль этой окружности,
а вектор
- касательный к окружности в каждой
точке, то
вдоль контура, совпадающего с выделенной
линией индукции магнитного поля
(окружностью на рис. 6.5). Обозначим
- радиус окружности. Так как величина
остается постоянной вдоль этой окружности,
а вектор
- касательный к окружности в каждой
точке, то
![]()
или, с учетом (6.6),
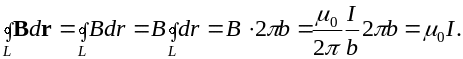 (6.14)
(6.14)
Можно
показать (см. Матвеев А.Н.), что формула
(6.14) остается справедливой, если в
качестве контура интегрирования выбрать
не линию индукции магнитного поля, а
произвольный замкнутый контур,
охватывающий провод с током. В частности,
если контур не охватывает провод с
током, то в (6.14) надо положить
![]() .
Тогда циркуляция
.
Тогда циркуляция
![]() .
.
Силу
тока в проводе выразим как интеграл от
плотности тока
![]() по поверхности
(см. рис. 1.19)):
по поверхности
(см. рис. 1.19)):
![]() (6.15)
(6.15)



Рис. 1.19. К формуле Стокса
Поверхность опирается на контур . Для постоянного тока величина интеграла в (6.15) не зависит от выбора формы поверхности в силу закона сохранения электрического заряда.
Подставим (6.15) в (6.14), найдем
![]() (6.16)
(6.16)
Из теории электромагнетизма следует, что формула (6.16) остается справедливой не только в случае прямолинейного тока, но и для произвольного распределения плотности постоянного тока на поверхности .
Пусть
имеется система токов, распределенных
в пространстве с плотностями
![]() ,
,
![]() .
Обозначим
.
Обозначим
![]() - индукция магнитного поля, созданного
- индукция магнитного поля, созданного
![]() ым
током. По принципу суперпозиции, индукция
результирующего поля
ым
током. По принципу суперпозиции, индукция
результирующего поля
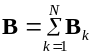 ,
а плотность результирующего тока
,
а плотность результирующего тока
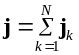 .
Применяя формулу (6.16) для
ого
тока, имеем:
.
Применяя формулу (6.16) для
ого
тока, имеем:
![]() (6.17)
(6.17)
где
![]() - сила тока
ой
компоненты через поверхность
,
- сила тока
ой
компоненты через поверхность
,
![]()
![]() (6.18)
(6.18)
Алгебраически
суммируя равенства (6.17) по
от
![]() до
до
![]() ,
получим
,
получим
![]() (6.19)
(6.19)
где
сила полного тока через поверхность
,
равная
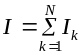 .
.
Равенство (6.19) выражает формулу полного тока в интегральной форме.
Применим
формулу Стокса для магнитного поля:
поток
вихря
![]() векторного поля
через кусочно-гладкую поверхность
,
ограниченную замкнутым контуром
,
равен циркуляции вектора
по этому контуру.
векторного поля
через кусочно-гладкую поверхность
,
ограниченную замкнутым контуром
,
равен циркуляции вектора
по этому контуру.
![]() (6.20)
(6.20)
Подставим (6.16) в (6.20), найдем
![]()
откуда в силу произвольности выбора поверхности следует
![]() (6.21)
(6.21)
Равенство
(6.21) выражает формулу полного тока в
дифференциальной форме. Из (6.21) следует,
что в области, где нет токов (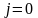 )
имеем:
)
имеем:
 .
Аналогично условию
.
Аналогично условию
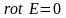 для электростатического поля равенство
выражает условие потенциальности
постоянного магнитного поля в области,
где нет токов.
для электростатического поля равенство
выражает условие потенциальности
постоянного магнитного поля в области,
где нет токов.
Применим
формулу полного тока (6.19) для расчета
магнитного поля внутри тороидальной
катушки, показанной на рис. 6.7. По виткам
катушки течет постоянный ток силой
.
Пунктирная окружность радиуса
![]() ,
имеющая общий центр с катушкой,
соответствует одной линий индукции
магнитного поля катушки. Внутренний
радиус катушки
,
имеющая общий центр с катушкой,
соответствует одной линий индукции
магнитного поля катушки. Внутренний
радиус катушки
![]() ,
а внешний -
,
а внешний -
![]() .
В силу симметрии катушки индукция
магнитного поля постоянна по величине
вдоль пунктирной окружности. Значит
циркуляция индукции вдоль этой линии
индукции
.
В силу симметрии катушки индукция
магнитного поля постоянна по величине
вдоль пунктирной окружности. Значит
циркуляция индукции вдоль этой линии
индукции
![]() .
Та же окружность охватывает ток силой
.
Та же окружность охватывает ток силой
![]() ,
где
- число витков катушки. По формуле полного
тока имеем:
,
где
- число витков катушки. По формуле полного
тока имеем:
![]() .
Значит, индукция магнитного поля
тороидальной катушки на расстоянии
от ее центра равна
.
Значит, индукция магнитного поля
тороидальной катушки на расстоянии
от ее центра равна
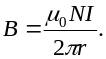

Рис. 6.7. Тороидальная катушка
Будем
неограниченно увеличивать радиус
тороида. Тогда отношение
![]() ,
и поле стремится к однородному. Любой
отрезок тороида стремится по форме к
прямолинейной катушке – соленоиду.
Заметим, что
,
и поле стремится к однородному. Любой
отрезок тороида стремится по форме к
прямолинейной катушке – соленоиду.
Заметим, что
![]() - число витков на единицу длины соленоида,
что дает выражение индукции магнитного
поля соленоида:
- число витков на единицу длины соленоида,
что дает выражение индукции магнитного
поля соленоида:
![]()
