
- •1.1. Событие и эксперимент. Соотношения между событиями. Пространство элементарных исходов
- •1.2. Относительная частота и вероятность события. Статистическое определение вероятности
- •1.3. Классическое определение вероятности
- •1.4. Геометрическое определение вероятности
- •1.5. Аксиоматика теории вероятностей
- •1.6. Условная вероятность. Независимость событий. Теорема умножения вероятностей
- •1.7. Теорема сложения вероятностей
- •1.8. Формула полной вероятности
- •1.9. Формула Байеса
- •1.10. Вычисление вероятностей в схеме повторных независимых испытаний
- •2.1. Понятие случайной величины. Дискретные и непрерывные величины
- •2.2. Ряд и многоугольник распределения дискретной св
- •2.3. Функция распределения св и её свойства
- •2.4. Плотность распределения непрерывной св и её свойства
- •2.5. Математическое ожидание, мода и медиана св
- •2.6. Моменты, дисперсия и среднее квадратическое отклонение св
- •2.7. Биномиальное распределение
- •2.8. Распределение Пуассона
- •3.2. Ряд, функция и плотность распределения случайного вектора
- •3.3. Условные законы распределения
- •3.4. Независимость случайных величин
- •3.5. Коррел-й момент и коэффициент корреляции системы двух св
- •4.1. Закон распределения функции случайного аргумента
- •4.2. Математическое ожидание и дисперсия функции св
- •4.3. Основные свойства математического ожидания
- •4.4. Основные свойства дисперсии
- •5.1. Закон больших чисел
- •5.2. Центральная предельная теорема
- •6.1. Основные понятия теории случайных процессов
- •6.2. Основные характеристики случайных процессов
- •6.3. Стационарные случайные процессы
4.1. Закон распределения функции случайного аргумента
Пусть имеется СВ Х с заданным законом
распределения. Другая СВ Y связана с СВ
Х зависимостью
![]() ,
где
,
где
![]() ‑ задана.
‑ задана.
Х – дискретная СВ с возможными значениями
и их вероятностями
.
Определим
![]() и построим ряд распределения СВ Y.
и построим ряд распределения СВ Y.
Теорема. Пусть Х – непрерывная СВ
с плотностью вероятности
,
а
![]() – дифференцируемая строго монотонная
(возрастающая или убывающая) функция.
Тогда плотность вероятности
– дифференцируемая строго монотонная
(возрастающая или убывающая) функция.
Тогда плотность вероятности
![]() СВ Y определяется равенством
СВ Y определяется равенством
![]() ,
,
где
![]() – функция, обратная к
.
– функция, обратная к
.
4.2. Математическое ожидание и дисперсия функции св
Пусть имеется СВ Х с заданным законом распределения. Другая СВ Y связана с СВ Х зависимостью , где – заданная функция.
Если Х – дискретная СВ с возможными значениями и их вероятностями , то математическое ожидание и дисперсия СВ Y определяются по формулам
![]() ,
,
![]() .
.
Если Х – непрерывная СВ с плотностью вероятности , то
![]() ,
,
![]() .
.
Пусть
– случайный вектор, а СВ Z связана с Х и
Y зависимостью
![]() ,
где
,
где
![]() – заданная функция. Тогда если Х и Y –
дискретные СВ с возможными значениями
– заданная функция. Тогда если Х и Y –
дискретные СВ с возможными значениями
![]() и
и
![]() и известны вероятности
и известны вероятности
![]() ,
,
![]() ,
,
то
,
,
то
![]() ,
,
![]() .
.
Если Х и Y – непрерывные СВ и известна плотность , то
![]() ,
,
![]() .
.
4.3. Основные свойства математического ожидания
1. Если с – константа, то
![]() .
.
2. Если с – константа, Х – СВ, то
![]() .
.
3. Если Х и Y – две СВ, то
![]() .
.
по индукции можно получить равенство
 .
.
4. Если Х и Y – две СВ, то
![]() .
.
Если Х и Y не коррелированны, то
![]() .
Если
– независимые СВ, то
.
Если
– независимые СВ, то
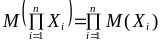 .
.
4.4. Основные свойства дисперсии
1. Если с – константа, то
![]() .
.
2. Если с – константа, Х – СВ, то
![]() .
.
3. Если Х и Y – произвольные СВ, то
![]() ,
,
![]() .
.
Если Х и Y не коррелированные, то
![]() .
Или
– независимые СВ, то
.
Или
– независимые СВ, то
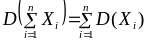 .
.
5.1. Закон больших чисел
Если Х – СВ с математическим ожиданием
![]() и дисперсией
и дисперсией
![]() ,
то
,
то
![]() (
неравенство Чебышева).
(
неравенство Чебышева).
Теорема Чебышева. Если
– случайные величины, которые независимы,
одинаково распределены и имеют
математическое ожидание m и дисперсию
D, то при неограниченном увеличении
n случайная величина
![]() сходится по вероятности к константе m,
т.е.
сходится по вероятности к константе m,
т.е.
![]() .
.
Доказательство. Рассмотрим СВ
![]() .
В силу свойств математического ожидания
и дисперсии и независимости
имеем
.
В силу свойств математического ожидания
и дисперсии и независимости
имеем
![]() и
и
![]() ,
поэтому неравенство Чебышева для СВ
,
поэтому неравенство Чебышева для СВ
![]() при произвольном
при произвольном
![]() будет иметь вид
будет иметь вид
![]() .
Правая часть при увеличении n
стремится к нулю, откуда следует
справедливость утверждения теоремы.
.
Правая часть при увеличении n
стремится к нулю, откуда следует
справедливость утверждения теоремы.
Теорема Бернулли. Если
![]() – относительная частота появления
некоторого события А в n независимых
испытаниях, в каждом из которых событие
А появляется с некоторой вероятностью
р, то при неограниченном увеличении
n относительная частота
сходится по вероятности к константе p,
т.е.
– относительная частота появления
некоторого события А в n независимых
испытаниях, в каждом из которых событие
А появляется с некоторой вероятностью
р, то при неограниченном увеличении
n относительная частота
сходится по вероятности к константе p,
т.е.
![]() .
.
Пусть через
![]() число появлений события А в i-м
испытании. Очевидно,
,
число появлений события А в i-м
испытании. Очевидно,
,
![]() – дискретные СВ с возможными значениями
0 и 1, при этом
– дискретные СВ с возможными значениями
0 и 1, при этом
![]() ,
,
![]() ,
.
В силу независимости испытаний, СВ
независимы, при этом
,
.
В силу независимости испытаний, СВ
независимы, при этом
![]() ,
,
![]() ,
,
![]() и
и
![]() Применяя теорему Чебышева к СВ
,
получим утверждение теоремы Бернулли.
Применяя теорему Чебышева к СВ
,
получим утверждение теоремы Бернулли.
5.2. Центральная предельная теорема
Теорема Ляпунова. Если
– случайные величины, которые независимы,
одинаково распределены и имеют
математическое ожидание m и среднее
квадратическое отклонение ,
то при неограниченном увеличении n
случайная величина
![]() сходится по распределению к величине
сходится по распределению к величине
![]() ,
т.е.
,
т.е.
![]() .
.
Замечание. При условиях, сформулированных
в теореме, закон распределения СВ
![]() при увеличении n приближается к
при увеличении n приближается к
![]() ,
а закон распределения СВ
,
а закон распределения СВ
![]() – к
– к
![]() ,
т.е.
,
т.е.
![]() .
.
При большом числе независимых измерений СВ Х закон распределения суммы и среднего арифметического результатов измерений близок к нормальному.
Теорема Лапласа. Если
![]() – число появлений некоторого события
А в n независимых испытаниях, в каждом
из которых это событие появляется с
вероятностью р, то при неограниченном
увеличении n случайная величина
– число появлений некоторого события
А в n независимых испытаниях, в каждом
из которых это событие появляется с
вероятностью р, то при неограниченном
увеличении n случайная величина
![]() сходится по распределению к случайной
величине
.
сходится по распределению к случайной
величине
.
Замечание. Из теоремы следует, что закон
распределения СВ
![]() при увеличении n приближается к
при увеличении n приближается к
![]() ,
а закон распределения относительной
частоты
,
а закон распределения относительной
частоты
![]() – к
– к
![]() ,
т.е.
,
т.е.
![]() ,
где
.
,
где
.
