3.2. Ряд, функция и плотность распределения случайного вектора

Рассмотрим дискретный случайный вектор . Пусть и – возможные значения СВ Х и Y соответственно, при этом и . Пусть , , , где . Ряд распределения случайного вектора .

Х Y			. . .
			. . .
			. . .
. . .	. . .	. . .	. . .	. . .
			. . .

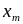
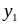
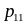
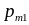
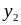
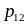
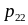
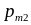
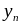
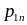
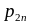
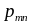
Вероятности отдельных значений каждой из СВ Х и Y определяются так:

; .

Пусть – произвольный случайный вектор. Тогда функция называется функцией распределения случайного вектора .

Пусть, далее, – непрерывный случайный вектор. ‑ плотность распределения вектора. Если известна плотность вероятности , то , а вероятность попадания в двумерную область D вычисляется по формуле .

, ,

,

Случай n-мерного случайного вектора :

, .

3.3. Условные законы распределения

ДСВ ‑ . Если у – одно из возможных значений СВ Y, то условным законом распределения СВ Х при называется совокупность условных вероятностей , , где – возможные значения СВ Х, – возможные значения СВ Y

, , ,

где , и , . Из этих равенств вытекают , , , .

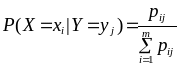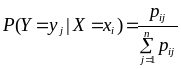– произвольный случайный вектор, а у – одно из возможных значений СВ Y. Условная функция распределения СВ Х при

, Y – дискретная СВ, и функция

,

Y – непрерывная СВ. Аналогично определяется .

– непрерывный случайный вектор и у – одно из возможных значений СВ Y. называется условной плотностью распределения СВ Х при . Теорема умножения плотностей распределения.

,

3.4. Независимость случайных величин

СВ Х называется независимой от СВ Y, если закон распределения СВ Х не зависит от того, какое значение принимает СВ Y, . Если – дискретный случайный вектор, то будут также справедливы равенства , , , а если непрерывный вектор – равенство . В противном случае СВ Х называется зависимой от СВ Y. Зависимость (независимость) СВ всегда взаимна.

Теорема. Случайные величины Х и Y независимы в том и только в том случае, если выполняется равенство .

Следствие 1. Дискретные СВ Х и Y независимы в том и только в том случае, если выполняются равенства

, , .

Следствие 2. Непрерывные СВ Х и Y независимы в том и только в том случае, если выполняется равенство .

3.5. Коррел-й момент и коэффициент корреляции системы двух св

Пусть – система двух СВ. называется корреляционным моментом СВ Х и Y.

Для дискретных СВ ,

для непрерывных .

Если , то величины Х и Y называются положительно коррелированными, если – отрицательно коррелированными, если – некоррелированными.

Теорема 1. Если СВ Х и Y независимы, то они не коррелированны.

Утверждение, обратное данному, не всегда верно: из некоррелированности двух СВ в общем случае не следует их независимость.

Нормированный корреляционный момент , где и .

Теорема 2. Для любых двух СВ Х и Y имеет место , причём в том и только в том случае, если одна из этих СВ является линейной функцией от другой.