
- •1.1. Событие и эксперимент. Соотношения между событиями. Пространство элементарных исходов
- •1.2. Относительная частота и вероятность события. Статистическое определение вероятности
- •1.3. Классическое определение вероятности
- •1.4. Геометрическое определение вероятности
- •1.5. Аксиоматика теории вероятностей
- •1.6. Условная вероятность. Независимость событий. Теорема умножения вероятностей
- •1.7. Теорема сложения вероятностей
- •1.8. Формула полной вероятности
- •1.9. Формула Байеса
- •1.10. Вычисление вероятностей в схеме повторных независимых испытаний
- •2.1. Понятие случайной величины. Дискретные и непрерывные величины
- •2.2. Ряд и многоугольник распределения дискретной св
- •2.3. Функция распределения св и её свойства
- •2.4. Плотность распределения непрерывной св и её свойства
- •2.5. Математическое ожидание, мода и медиана св
- •2.6. Моменты, дисперсия и среднее квадратическое отклонение св
- •2.7. Биномиальное распределение
- •2.8. Распределение Пуассона
- •3.2. Ряд, функция и плотность распределения случайного вектора
- •3.3. Условные законы распределения
- •3.4. Независимость случайных величин
- •3.5. Коррел-й момент и коэффициент корреляции системы двух св
- •4.1. Закон распределения функции случайного аргумента
- •4.2. Математическое ожидание и дисперсия функции св
- •4.3. Основные свойства математического ожидания
- •4.4. Основные свойства дисперсии
- •5.1. Закон больших чисел
- •5.2. Центральная предельная теорема
- •6.1. Основные понятия теории случайных процессов
- •6.2. Основные характеристики случайных процессов
- •6.3. Стационарные случайные процессы
1.6. Условная вероятность. Независимость событий. Теорема умножения вероятностей
Пусть А и В – два произвольных события.
Относительные частоты событий А, В и
в n повторения испытания выражаются
отношениями
,
![]() и
и
![]() ,
где
,
где
![]() – число появлений события
в n испытаниях. Обозначим через
– число появлений события
в n испытаниях. Обозначим через
![]() относительную частоту события А в тех
испытаниях, где появилось событие В, а
через
относительную частоту события А в тех
испытаниях, где появилось событие В, а
через
![]() – вероятность события А, вычисленная
при условии, что событие В произошло.
Поскольку
– вероятность события А, вычисленная
при условии, что событие В произошло.
Поскольку
![]() ,
,
то естественно положить
![]() и
и
![]() .
.
![]() ‑ произвольные событий А и В.
Независимость событий всегда взаимна.
‑ произвольные событий А и В.
Независимость событий всегда взаимна.
Теорема. Вероятность произведения
произвольных событий
вычисляется по формуле
![]()
![]() .
(математической индукцией).
.
(математической индукцией).
1.7. Теорема сложения вероятностей
Теорема. Вероятность суммы двух
произвольных событий А и В вычисляется
по формуле
![]() .
.
Если
то
![]() .
(Индукция)
.
(Индукция)
Доказательство.
![]() ,
,
![]() ,
,
![]() .
.
1.8. Формула полной вероятности
Пусть требуется найти вероятность
некоторого события А, которое может
произойти только совместно с одним из
событий
![]() ,
образующих полную группу попарно
несовместных событий (гипотез). Тогда
искомая вероятность вычисляется по
формуле
,
образующих полную группу попарно
несовместных событий (гипотез). Тогда
искомая вероятность вычисляется по
формуле
![]() ,
,
называемой формулой полной вероятности.
1.9. Формула Байеса
Пусть имеется полная группа попарно
несовместных событий (гипотез)
.
Вероятности этих гипотез до опыта
известны и равны
![]() .
Проведён опыт, в результате которого
произошло событие А. Требуется найти
условную вероятность
.
Проведён опыт, в результате которого
произошло событие А. Требуется найти
условную вероятность
![]() гипотезы
гипотезы
![]() после того как произошло событие А.
после того как произошло событие А.
Справедлива следующая формула, называемая формулой Байеса:
![]() ,
,
где .
Вероятность
![]() называется априорной вероятностью
гипотезы
,
а
– апостериорной вероятностью этой
гипотезы.
называется априорной вероятностью
гипотезы
,
а
– апостериорной вероятностью этой
гипотезы.
1.10. Вычисление вероятностей в схеме повторных независимых испытаний
Пусть есть событие А,
![]() ,
,
![]() .
Испытания повторяются независимо друг
от друга при неизменных условиях n
раз. Требуется найти вероятность
.
Испытания повторяются независимо друг
от друга при неизменных условиях n
раз. Требуется найти вероятность
![]() того, что при n повторениях испытания
событие А произойдёт ровно m раз
(
того, что при n повторениях испытания
событие А произойдёт ровно m раз
(![]() ).
Рассмотрим
).
Рассмотрим
![]() ,
где
,
где
![]() ,
,
![]() ,
. . . ,
,
. . . ,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
где
,
где
![]() .
.
![]() .
.
2.1. Понятие случайной величины. Дискретные и непрерывные величины
Случайной величиной (СВ) называется такая величина, которая в результате опыта может принять одно и только одно значение из некоторого подмножества числовой прямой.
Случайная величина Х называется дискретной, если она принимает только отдельные изолированные друг от друга значения с определёнными вероятностями. Множество возможных значений дискретной СВ может быть конечным или счётным.
Случайная величина Х называется непрерывной, если множество её возможных значений – конечный или бесконечный промежуток числовой прямой, причём вероятность появления каждого отдельного значения равна нулю.
2.2. Ряд и многоугольник распределения дискретной св
Пусть Х – дискретная СВ, которая в
результате опыта принимает одно из
значений
![]() ,
а
,
а
![]() ,
,
![]() – вероятности появления этих значений.
События
– вероятности появления этих значений.
События
![]() ,
являются, очевидно, попарно несовместными
и образуют полную группу, поэтому
,
являются, очевидно, попарно несовместными
и образуют полную группу, поэтому
 .
.
Законом распределения дискретной СВ
называется любое соотношение,
устанавливающее связь между её возможными
значениями
![]() и их вероятностями
и их вероятностями
![]() .
Простейшей формой задания закона
распределения дискретной СВ с конечным
множеством значений является следующая
таблица, называемая рядом распределения:
.
Простейшей формой задания закона
распределения дискретной СВ с конечным
множеством значений является следующая
таблица, называемая рядом распределения:
-
Х
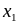

. . .
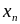
р
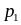
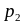
. . .
Предполагается, что
![]() .
Если множество возможных значений
.
Если множество возможных значений
![]() дискретной СВ счетное, то её ряд
распределения иногда удаётся представить
формулой вида
дискретной СВ счетное, то её ряд
распределения иногда удаётся представить
формулой вида
![]() ,
,
где р – некоторая функция и выполняется
условие
,
,
где р – некоторая функция и выполняется
условие
![]() .
.
