Энтропия и вероятность

Если макросистема находится в неравновесном состоянии, то она самопроизвольно будет переходить в состояние с большей вероятностью - равновесное. Вместе с тем, согласно второму началу термодинамики все самопроизвольные процессы в замкнутых макросистемах сопровождаются возрастанием энтропии. Поэтому можно ожидать, что между энтропией S макросистемы в каждом состоянии и вероятностью Р того же состояния должна существовать определенная связь. Эта идея, высказанная Больцманом, оправдалась и оказалась весьма плодотворной.

Для нахождения этой связи рассмотрим простой частный случай - необратимый процесс расширения идеального газа в пустоту. Пусть данный газ первоначально находился в объеме V₁ теплоизолированного сосуда объемом V₀. От остальной части сосуда он отделен перегородкой (рисунок). Перегородку практически мгновенно перемещают из положения 1 в 2, газ расширяется в пустоту до объема V₂ и приходит в равновесное состояние.

В данном случае работу газ не совершает (А = 0), переданное газу тепло Q = 0, следовательно, по первому началу приращение внутренней энергии U = 0, т.е. температура конечного и начального состояний одинакова.

Поскольку энтропия - функция состояния, то ее приращение в процессе V₁  V₂ можно вычислить по обратимому процессу, например, изотермическому. В изотермическом процессе Q = A = RT ln(V₂/V₁) и

S = Q/T = R ln(V₂/V₁) = kN ln(V₂/V₁)

где N - число молекул в газе.

Теперь обратимся к вероятностям. В рассмотренном процессе распределение по скоростям в начальном и конечном состояниях одинаково: оно зависит только от температуры Т, которая не изменилась. Пространственное же распределение молекул стало более «свободным», а значит и более вероятным. В самом деле, вероятность нахождения одной молекулы газа в объеме V₁ равна (V₁/V₀). Вероятность же всех N молекул собраться в объеме V₁ равна (V₁/V₀)^N. Обозначим эту вероятность как Р₁. Соответственно (V₂/V₀)^N - как Р₂. Тогда отношение этих вероятностей

Р₂/Р₁ = (V₂/V₁) ^N,

и приращение энтропии можно записать как

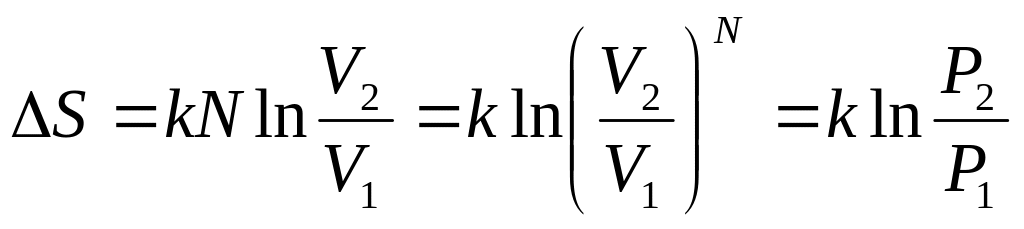
Поскольку вероятность состояния макросистемы пропорциональна ее статистическому весу, т.е. Р  , последнюю формулу представим так:

S = k ln(₂/₁)

и мы приходим к знаменитой формуле Больцмана

S = k ln

Приведенные выше рассуждения не претендуют на вывод этой формулы, а представляют собой скорее некоторые пояснения. Строгий вывод этой формулы дается в статистической физике. Можно доказать, что формула относится также и к неравновесным состояниям.

Теперь предположим, что макросистема состоит из двух практически не взаимодействующих подсистем, одна из которых находится в состоянии 1 с энтропией S₁ и статистическим весом ₁, а другая - в состоянии 2 с энтропией S₂ и статистическим весом ₂.

Число способов (микросостояний), которыми может реализоваться рассматриваемое состояние макросистемы, равно произведению числа способов, которыми могут быть осуществлены состояния каждой из подсистем в отдельности:

 = ₁₂

Отсюда следует, что S = k ln(₁₂) = k ln₁ + k ln₂ = S₁ + S₂, как и должно быть, поскольку энтропия - величина аддитивная.

Принцип возрастания энтропии со статистической точки зрения привел Больцмана к фундаментальному выводу:

все замкнутые макросистемы стремятся переходить от состояний менее вероятных к более вероятным.

Степень неопределенности состояния макросистемы, которая определяется числом микросостояний, которыми может реализоваться данное макросостояние, можно назвать степенью беспорядка в макросистеме.* Таким образом, энтропия S характеризует степень беспорядка в макросистеме: состояниям с большим беспорядком отвечает большая вероятность (или статистический вес ), чем у более упорядоченного состояния, а поэтому и большее значение энтропии.

Таким образом, реальные самопроизвольные тепловые процессы протекают так, что беспорядок в макросистеме увеличивается. С этим связан и тот факт, что любой вид энергии переходит в конце концов во внутреннюю энергию, т.е. в состояние, при котором «хаос» в макросистеме максимален. Это состояние является равновесным, его энтропия S = макс.

Каково бы ни было первоначальное состояние макросистемы (например, газа), будучи теплоизолированной она неизбежно переходит в состояние, при котором распределение молекул по скоростям будет максвелловским, а во внешнем поле еще и больцмановским.

*Вероятность какого-либо события может служить мерой его неожиданности. Качественно это довольно очевидно. Если вероятность мала, то событие осуществляется редко и, следовательно, относится к категории неожиданных. Наоборот, если вероятность близка к единице, то событие случается часто и с этой точки зрения относится к заурядным.

В теории информации за меру неожиданности события условились принимать натуральный логарифм его вероятности w, взятый с обратным знаком: ln w.

Выбранная таким образом мера неожиданности хорошо передает многие из наших интуитивных представлений о свойствах, которыми она должна обладать. Действительно, вероятность - величина, меньшая единицы, и, следовательно, ее логарифм, взятый со знаком минус, положителен, т.е. неожиданность - величина положительная. Если событие достоверно, то вероятность равна единице, а ее логарифм равен нулю, так что неожиданность достоверного события равна нулю. Наконец, если событие состоит из двух независимых простых, то, поскольку его вероятность равна произведению вероятностей, неожиданность сложного события равна сумме неожиданностей простых событий, из которых оно состоит.

Рассмотрим пример. Пусть в сосуде содержится три молекулы и в нем выделен объем, составляющий 0,1 от полного объема, т.е. V/V = 0,1. Какова неожиданность того, что в этом объеме окажутся все три молекулы? Вероятность такого события равна (V/V)³. Его неожиданность равна

ln (V/V)³ = 3 ln 10 = 6,9.

Этот же результат можно было получить несколько иначе. Рассматриваемое событие состоит в осуществлении трех независимых событий, а именно попадания каждой из трех молекул в V. неожиданность попадания одной молекулы равна ln w = ln 10 = 2,3. Неожиданность попадания трех молекул в три раза больше, т.е. получаем тот же результат.

Поскольку отношение V/V мало, то попадание молекул в V - маловероятное событие и поэтому гораздо менее удивительно, если все три молекулы окажутся вне V. Какова неожиданность этого события? Соответствующая вероятность равна (1  V/V)³ = 0,9³. Для неожиданности найдем

ln (1  V/V)³ = 0,3

Ее числовое значение в этом случае получилось значительно меньше, чем в предыдущем.

Пусть рассматривается некоторая полная группа несовместимых событий. Каждое из этих событий обладает своей неожиданностью, и возникает вопрос о характеристике, общей для всей системы. такая характеристика, называемая энтропией, вводится как среднее по всей системе значение неожиданностей, т.е. неожиданность каждого i-го события умножается на вероятность этого события W_i и все полученные результаты складываются. таким образом, обозначив энтропию S, можем записать математическое выражение, определяющее эту величину,

, где суммирование распространено на все события, составляющие полную группу (полная группа событий представляет собой все возможные исходы опыта. Сумма вероятностей таких событий равна единице). Энтропия характеризует степень неопределенности или хаотичности, которая имеет место в данной ситуации.

Рассмотрим пример, в котором молекула А может попасть или не попасть в объем V, находящийся в сосуде объема V.

Предположим вначале, что объем V очень мал по сравнению с V. Интуитивно ясно, что в этом случае неопределенность ситуации очень мала, так как почти наверняка молекула окажется вне V. Энтропия отражает это представление. Действительно, вероятность попадания в V есть W₁ = V/V, а вероятность непопадания W₂ = 1  (V/V). Для энтропии, следовательно, имеем

Предел этого выражения при V/V  0 равен 0 (неопределенность ноль на бесконечность в первом слагаемом можно раскрыть по правилу Лопиталя). Таким образом, при малом V/V значение энтропии мало.

Легко убедиться, что точно такое же положение имеет место, когда объем V стремится к V. В этом случае почти наверняка молекула А окажется в V. неопределенность такой ситуации мала, и значение энтропии оказывается снова близким к нулю.

Когда же достигается наибольшая неопределенность? Попытаемся ответить на этот вопрос, выяснив, при каких условиях энтропия достигает своего максимального значения, рассматривая ее как функцию вероятности W₁ = V/V. По общему правилу нахождения максимума функции продифференцируем S по вероятности и приравняем производную нулю, тогда получим

Отсюда W₁ = V/V = 1/2

Таким образом, наиболее неопределенное положение достигается тогда, когда V составляет половину объема V.

Итак, мерой неопределенности или хаотичности ситуации, характеризуемой некоторой полной группой несовместимых событий с вероятностями W₁, служит функция этих вероятностей

называемая информационной энтропией.