
- •Основные понятия теории вероятностей: испытание, событие. Классификация событий. Полная группа событий. Примеры.
- •Вероятность. Классическое определение вероятности. Использование формул комбинаторики. Примеры.
- •Статическое определение вероятности.
- •Формула полной вероятности. Формула Байеса. Примеры.
- •Повторение независимых испытаний. Формула Бернулли. Примеры.
- •Повторение независимых испытаний. Асимптотические формулы. Локальная и интегральная теоремы Лапласа. Примеры.
- •Дискретные случайные величины. Закон распределения. Полигон распределения. Примеры построения дискретной случайной величины.
- •Числовые хар-ки дискретной случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение. Примеры.
- •Свойства математического ожидания и дисперсии. Математическое ожидание и дисперсия среднего значения. Примеры.
- •Биномиальное распределение. Распределение Пуассона. Геометрическое распределение. Их числовые хар-ки. Примеры.
- •Непрерывная случайная величина. Функции распределения. Плотность вероятностей. Их свойства. Вероятность попадания в заданный интервал. Примеры.
- •Числовые хар-ки непрерывной случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение, мода, медиана. Примеры.
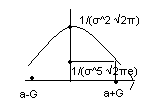
- •Равномерное распределение. Нормальное распределение. Функции Гаусса и Лапласа. Их числовые хар-ки. Примеры.
- •Вероятность попадания в заданный интервал нормально распределенной случайной величины. Отыскание интервала по заданной вероятности. Примеры.
- •Понятие о центральной предельной теореме Ляпунова.
- •Понятие о случайном процессе. Система массового обслуживания как случайный процесс.
- •Случайный процесс со счетным множеством состояний. Виды. Система массового обслуживания с необратимыми и обратимыми переходами состояний.
- •Поток событий. Простейший поток и его свойства. Виды потоков событий.
- •Марковский случайный процесс.
- •Понятие о методе Монте-Карло.
- •Математическая статистика. Генеральная и выборочная совокупности. Репрезентативность выборки. Вариационные ряды. Полигон и гистограмма. Примеры.
- •Оценка числовых хар-к. Состоятельность, несмещенность и эффективность оценок. Оценка математического ожидания. Примеры.
- •Выборочная и исправленная дисперсии. Другие хар-ки вариации данных. Исправленная дисперсия среднего значения. Примеры.
- •Интервальные оценки. Доверительный интервал для оценки математического ожидания. Распределение Стьюдента.
- •Статистическая, корреляционная и функциональная зависимости. Уравнения регрессии. Примеры.
- •Коэффициент корреляции и его свойства. Нахождение уравнений регрессии по корреляционной таблице. Примеры.
Непрерывная случайная величина. Функции распределения. Плотность вероятностей. Их свойства. Вероятность попадания в заданный интервал. Примеры.
Для
непрерывной случайной величины построение
таблицы распределения невозможно.
Поэтому для задания используют ф-ию
распределения. Пусть Х – нсв, Х![]() R,
Х<x.
Вер-ть этого события есть ф-ия от х.
F(x)=P(X<x).
Интегральная ф-ия распределения нсв Х
– ф-ия F(x),
равная вер-ти того, что в рез-те испытаний
случайная величина Х примет значение
меньше х. Геометрическая интерпретация:
F(x)
есть вер-ть того, что случайная величина
примет значение, кот изображено на
числовой оси точкой, лежащей левее точки
х. НСВ назыв случайной величиной, если
ф-ия распределения есть непрерывная,
кусочно дифференцируемая ф-ия с
непрерывной производной. Св-ва ф-ии
интегрального распределения: 1) значения
ф-ии распределения принадлежат отрезку
[0;1]:
R,
Х<x.
Вер-ть этого события есть ф-ия от х.
F(x)=P(X<x).
Интегральная ф-ия распределения нсв Х
– ф-ия F(x),
равная вер-ти того, что в рез-те испытаний
случайная величина Х примет значение
меньше х. Геометрическая интерпретация:
F(x)
есть вер-ть того, что случайная величина
примет значение, кот изображено на
числовой оси точкой, лежащей левее точки
х. НСВ назыв случайной величиной, если
ф-ия распределения есть непрерывная,
кусочно дифференцируемая ф-ия с
непрерывной производной. Св-ва ф-ии
интегрального распределения: 1) значения
ф-ии распределения принадлежат отрезку
[0;1]: ![]() .
Док-во: вер-ть всегда есть неотрицательное
число, не превышающее единицы. 2) F(x)
– неубывающая ф-ия, т.к.
.
Док-во: вер-ть всегда есть неотрицательное
число, не превышающее единицы. 2) F(x)
– неубывающая ф-ия, т.к. ![]() ,
отсюда
,
отсюда ![]() .
Док-во:
.
Док-во: ![]() .
.
![]() ,
или
,
или ![]() .
Т.к. любая вер-ть есть число неотрицательное,
то
.
Т.к. любая вер-ть есть число неотрицательное,
то ![]() ,
что и требовалось доказать. Следствие
1: Вер-ть того, что случайная величина
примет значение, заключенное в интервале
(a,b),
равна приращению ф-ии распределения на
этом интервале: если
,
что и требовалось доказать. Следствие
1: Вер-ть того, что случайная величина
примет значение, заключенное в интервале
(a,b),
равна приращению ф-ии распределения на
этом интервале: если ![]() ,
то
,
то ![]() .
Пр: Случайная величина Х задана ф-ей
распределения
.
Пр: Случайная величина Х задана ф-ей
распределения
![]()
Найти
вер-ть, того что в результате испытания
Х примет значение, принадлежащее
интервалу (0,2): ![]() .
Решение: т.к. на интервале (0,2), по условию
F(x)=
.
Решение: т.к. на интервале (0,2), по условию
F(x)=![]() ,
то
,
то ![]() .
Получим
.
Получим ![]() .
Следствие 2: Вер-ть того, что нсв Х примет
одно определенное значение равно 0: если
.
Следствие 2: Вер-ть того, что нсв Х примет
одно определенное значение равно 0: если
![]() ,
то
,
то ![]() .
.![]() .
3) если возможные значения случайной
величины принадлежат интервалу (a,b),
то: 1) F(x)=0,
при
.
3) если возможные значения случайной
величины принадлежат интервалу (a,b),
то: 1) F(x)=0,
при ![]() ;
2) F(x)=1,
при
;
2) F(x)=1,
при ![]() .
Док-во: 1) пусть
.
Док-во: 1) пусть ![]() ,
тогда
,
тогда ![]() невозможно (т.к. значений меньше
,
величина Х по условию не принимает) и,
следовательно, вер-ть его равна 0. 2) пусть
невозможно (т.к. значений меньше
,
величина Х по условию не принимает) и,
следовательно, вер-ть его равна 0. 2) пусть
![]() ,
тогда событие
,
тогда событие ![]() достоверно (т.к. все возможные значения
Х меньше
).
Следствие: если возможные значения нсв
расположены на всей оси х, то справедливы
следующие предельные соотношения:
достоверно (т.к. все возможные значения
Х меньше
).
Следствие: если возможные значения нсв
расположены на всей оси х, то справедливы
следующие предельные соотношения: ![]() .
.
НСВ
м также задать, используя ф-ию, кот назыв
плотностью распределения или плотностью
вер-ти (дифференцируемая ф-ия распределения
нсв). Плотность распределения вер-тей
нсв Х – ф-ия f(x)
– первая производная от ф-ии распределения
F(x):
![]() .
Ввиду того, что F(x)
– неубывающая ф-ия,
.
Ввиду того, что F(x)
– неубывающая ф-ия, ![]() .
F(x)
– первообразная от f(x).
Теорема: Вер-ть того, что нсв Х примет
значение, принадлежащее интервалу
(a,b),
равна определенному интегралу от
плотности распределения, взятому в
пределах от a
до b:
.
F(x)
– первообразная от f(x).
Теорема: Вер-ть того, что нсв Х примет
значение, принадлежащее интервалу
(a,b),
равна определенному интегралу от
плотности распределения, взятому в
пределах от a
до b:
![]() .
Док-во:
.
Док-во: ![]() - формула Ньютона-Лейбница. Геометрическая
интерпретация:
- формула Ньютона-Лейбница. Геометрическая
интерпретация: ![]() представляет собой площадь прямоугольной
трапеции, ограниченной графиком y=f(x),
отрезками y=0,
x=a
и x=b.
Следствие: если f(x)
– четная ф-ия и концы интервала симметричны
относительно начала координат, то:
представляет собой площадь прямоугольной
трапеции, ограниченной графиком y=f(x),
отрезками y=0,
x=a
и x=b.
Следствие: если f(x)
– четная ф-ия и концы интервала симметричны
относительно начала координат, то: ![]() .
Пр: задана плотность вер-ти случайной
величины Х
.
Пр: задана плотность вер-ти случайной
величины Х
![]() . Найти вер-ть того, что в рез-те испытания
Х примет значение, принадлежащее
интервалу (0,5;1). Решение: искомая вер-ть
. Найти вер-ть того, что в рез-те испытания
Х примет значение, принадлежащее
интервалу (0,5;1). Решение: искомая вер-ть
![]() .
Св-ва: 1) плотность распределения –
неотрицательная ф-ия:
.
Св-ва: 1) плотность распределения –
неотрицательная ф-ия: ![]() .
График плотности распределения назыв
кривой распределения. 2) несобственный
интеграл от плотности распределения в
пределах от
.
График плотности распределения назыв
кривой распределения. 2) несобственный
интеграл от плотности распределения в
пределах от ![]() до
до ![]() равен 1:
равен 1: ![]() .
Этот интеграл выражает вер-ть события,
состоящего в том, что случайная величина
примет значение, принадлежащее интервалу
(
.
Этот интеграл выражает вер-ть события,
состоящего в том, что случайная величина
примет значение, принадлежащее интервалу
(![]() ).
Это событие явл достоверным, и его вер-ть
равна 1. Геометрически это означает, что
вся площадь криволинейной трапеции,
ограниченной осьб Ох и кривой распределение,
равна 1. В частности, если все возможные
значения случайной величины принадлежат
интервалу (а,b),
то
).
Это событие явл достоверным, и его вер-ть
равна 1. Геометрически это означает, что
вся площадь криволинейной трапеции,
ограниченной осьб Ох и кривой распределение,
равна 1. В частности, если все возможные
значения случайной величины принадлежат
интервалу (а,b),
то ![]() .
.
