§2. Линейные пространства и линейные операторы

В этом пособии уже встречались множества, в которых были определены операции сложения и умножение на число. В главе 1 для числовых матриц одинакового вида были определены операция сложения и операция умножения на число. Кроме того, для матриц одинакового вида были определены нулевая матрица и противоположные матрицы. В главе 2 рассматривались геометрические векторы, которые тоже можно складывать между собой и умножать на число. Для них определены нулевой вектор и противоположные векторы. В каждом из указанных случаев эти операции определялись по-своему, но они имели одни и те же свойства: коммутативность и ассоциативность сложения, дистрибутивность умножения на число по отношению к сложению и т. д. И часто эти свойства использовались при выполнении сложных действий над матрицами или векторами без каких-либо ссылок на определение этих операций, Существуют и другие разнообразные примеры множеств, элементы которых обладают такими же свойствами. В связи с этим возникла необходимость исследовать множество, состоящее из элементов, какой угодно природы, в котором определены операция сложения и операция умножения на число. И эти операции должны обладать указанным набором свойств. Такие множества получили название линейное или векторное пространство. Одной из важных задач, связанных с этими пространствами, является изучение прямых линий, плоских и выпуклых множеств и базисов.

Теория линейных операторов занимает большое место в теории векторных пространств. Линейный оператор – это отображение векторного пространства, согласованное с его линейной структурой. Это понятие является главным в линейной алгебре, и играет важную роль в самых разнообразных областях математики и физики. И основным аналитическим аппаратом линейных операторов является матричная запись.

Определение 4. Множество L называется линейным пространством, а его элементы  векторами, если:

1) задан закон, по которому любым двум элементам х и у из L сопоставлен элемент множества L, называемый их суммой и обозначаемый х + у;

2) задан закон, по которому элементу х из L и числу k сопоставлен элемент множества L, называемый произведением х на k и обозначаемый k×х;

3) выполнены следующие аксиомы:

1. ("х, у) (х + у = у + х), (коммутативность)

2. ("х у, z)((х + у) + z = x + (y + z)), (ассоциативность)

3. $0"х( х + 0 = х), (существование нулевого вектора)

4. "х $(–х)( х + (х) = 0), (существование противоположного вектора)

5. ("х, у) ("k) (k×(х+у) = k×х+ k×у), (дистрибутивность)

6. ("х) ("k, m) ((k + m)×х = k×х + m×х), (дистрибутивность)

7. ("х) ("k, m) k×(m×х) = (k× m)×х, (ассоциативность)

8. ("х) (1×х = х). (свойство единицы)

Здесь и далее буквы х, у, z обозначают векторы из L, буквы k, m обозначают вещественные числа, 0 – нулевой вектор, (–х) – вектор, противоположный вектору х.

Пример 8. Множество всевозможных числовых строк длины n называется nмерным векторным пространством и обозначается Rⁿ . Его элементы (x₁, x₂, … , x_n) называются n–мерными числовыми векторами, при этом числа x₁, x₂, … , x_n называются координатами этого вектора. Отношение равенства и операции сложение векторов и умножение вектора на число такие же, как у матриц:

(x₁, x₂, … , x_n) = (y₁, y₂, … , y_n) Û x₁= у₁, x₂= у₂, … , x_n= y_n ;

(x₁, x₂, … , x_n) + (y₁, y₂, … , y_n) = (x₁+ y₁, x₂+ y₂, … , x_n+ y_n);

k× (x₁, x₂, … , x_n) = (k×x₁, k×x₂, … , k×x_n).

Кроме того, (0, 0, … , 0)  нулевой вектор, (x₁, x₂, … , x_n)  вектор, противоположный вектору (x₁, x₂, … , x_n). В главе 1 §1 было показано, что матрицы обладают свойствами, соответствующими указанным выше аксиомам, поэтому Rⁿ является линейным пространством. Для удобства изложения n–мерные числовые векторы часто определяются как числовые матрицы-столбцы.

В главе 1 §5 для строк и столбцов были введены понятия линейной зависимости и независимости и понятие базиса. Эти определения сохраняются для числовых векторов. Более того, аналогичные понятия определяются в произвольном векторном пространстве L.

Определение 5. Пусть х₁, х₂, …, х_k - векторы из L. Линейной комбинацией этих векторов называется выражение m₁×х₁ + m₂×х₂ + …+ m_k×х_k, где m₁, m₂, …, m_k - числовые коэффициенты. Векторы называются линейно зависимыми, если существует их линейная комбинация, которая равна нулевому вектору и в которой имеются коэффициенты, отличные от нуля. В противном случае векторы называются линейно независимыми. Если некоторый вектор у равен линейной комбинации m₁×х₁ + m₂×х₂ + …+ m_k×х_k, то говорят, что у линейно выражается через векторы х₁, х₂, …, х_k . Базисом в пространстве L называется упорядоченная конечная система векторов, если она линейно независима и каждый вектор из L линейно выражается через векторы этой системы.

Пусть е₁, е₂, …, е_n – базис пространства L, и вектор y равен линейной комбинации m₁×е₁ + m₂×е₂ + …+ m_n×е_n, тогда коэффициенты m₁, m₂, …, m_т называются координатами вектора y. Принято обозначать базис в виде строки`е = (е<sub>1</sub>, е<sub>2</sub>, …, е<sub>n</sub>) и координаты вектора х по базису `е в виде столбца:

`m = который называется координатным столбцом вектора y.

Понятие умножение числовых матриц можно распространить на матрицы`е и `m, тогда вектор y представим в виде: y =`е×`m. Легко проверяются следующие утверждения.

Теорема 1. 1). Если задан базис, то координаты вектора определяются однозначно.

2). Координатный столбец суммы векторов равен сумме координатных столбцов векторов-слагаемых.

3). Координатный столбец произведения вектора на число равен произведению координатного столбца данного вектора на это число.

Из этой теоремы следует, что векторы линейно зависимы тогда и только тогда, когда линейно зависимы их координатные столбцы.

Пример 9. В пространстве R³ определить, являются ли векторы `а,`b,`c линейно зависимыми, где:

1) `а = (1, 4, 6),`b = (1, 1, 1),`c = (1, 1, 3);

2) `а = (2, 3, 1),`b = (3, 1, 5),`c = (1, 4, 3).

Решение. 1). Сначала подбираются числа x₁, x₂, x₃ такие, что x₁×`а + x<sub>2</sub>×`b + x₃×`c =`0. Для наглядности векторы записываются в виде столбцов, тогда предыдущее равенство записывается в виде:

x₁× + x₂× + x₃× = .

x₁ + x₂ + x₃ = 0,

А это равносильно системе: 4×x₁  x₂ + x₃ = 0,

6×x₁ + x₂ + 3×x₃ = 0.

Д ля решения системы находится ее определитель: Так как определитель равен 0, то по его строчки линейно зависимые и, следовательно, данные векторы линейно зависимые. Например, линейная комбинация 2`а + 3`b  5`c равна`0, действительно:

2 + 3  5 = = .

2). Сначала подбираются числа x₁, x₂, x₃ такие, что x₁×`а + x<sub>2</sub>×`b + x₃×`c =`0. Это равенство записывается в виде:

x₁× + x₂× + x₃× = .

2x₁ + 3x₂ + x₃ = 0,

А это равносильно системе: 3x₁  x₂ 4x₃ = 0,

 x₁ + 5х₂ + 3х₃ = 0.

Для решения системы находится ее определитель:

С ледовательно, система имеет единственное решение, которое вычисляется по формулам (5). Здесь свободные члены равны 0, поэтому все вспомогательные определители равны 0. Поэтому единственным решением системы являются x₁ = 0, x₂ = 0, x₃ = 0. Это означает, что данные векторы `а,`b,`c линейно независимые.

Определение 6. Линейное пространство называется n-мерным, если в нем существует базис из n векторов.

Пример 10. 1). Множество всех геометрических векторов на плоскости является 2-мерным линейным пространством. Его базис образуют орты `i и`j.

2). Множество всех геометрических векторов в пространстве является 3-мерным линейным пространством. Его базис образуют орты `i ,`j и`k.

3). Пространство Rⁿ является n-мерным линейным пространством. Его базис образуют числовые векторы:

(1, 0, 0, … , 0), (0, 1, 0, … , 0), (0, 0, 1, … , 0), … , (0, 0, 0, … , 1).

Теорема 2. В n-мерном линейном пространстве каждая упорядоченная система из n линейно независимых векторов является базисом.

Пример 11. Среди 4 векторов `а,`b,`c,`d пространства R³ выбрать базис и выразить четвертый вектор через базисные, где `а = (1, 4, 0),`b =

(2, 7, 1),`c = (3, 10, 3),`d = (2, 11, 1).

Решение. 1). Данные векторы записываются в виде матрицы:

.

С помощью эквивалентных преобразований, описанных в главе 1, эта матрица приводится к виду трапеции (9).

1-й шаг. 1-я строка умножается последовательно на числа -2, -3, -2 и прибавляется соответственно к 2-й, 3-й, 4-й строкам:

.

2-й шаг. 2-я строка последовательно умножается на 2, 3 и прибавляется к 3-й, 4-й строкам:

.

3-й шаг. Здесь очевидно, что минор, расположенный на 1-й, 2-й, 3-й строках, отличен от 0, поэтому эти строчки линейно независимые, и соответствующие им векторы `а,`b,`c можно взять за базис. 4-й шаг. Чтобы выразить вектор `d через этот базис подбираются числа x₁, x₂, x₃ такие, что x₁×`а + x<sub>2</sub>×`b + x₃×`c =`d . Это равенство записывается в виде:

x₁× + x₂× + x₃× = .

А это равносильно следующей системе линейных уравнений:

x₁ + 2x₂ + 3x₃ = 2,

 4×x₁ + 7x₂ + 10x₃ = 11,

x₂ + 3×x₃ = 1.

Для решения системы применяется метод Гаусса. 1-е уравнение умножается на 4 и прибавляется ко 2-му уравнению:

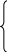x₁ + 2x₂ + 3x₃ = 2,

 x₂  2x₃ = 3,

x₂ + 3×x₃ = 1.

Теперь к 3-му уравнению прибавляется 2-е уравнение и получается система в треугольном виде:

x₁ + 2x₂ + 3x₃ = 2,

 x₂  2x₃ = 3,

x₃ = 4.

В 3-м уравнении получено x₃ = 4. Это значение подставляется во 2-е уравнение и находится значение для x₂: x₂ = (3 + 24) = 11. Далее, найденные значения подставляются в 1-е уравнение: x₁ = 2 2(11)  34 = 12. Таким образом, `d = 12×`а  11×`b + 4×`c .

Определение 7. Линейным преобразованием векторного пространства L называется однозначное отображение А вида L Þ L, удовлетворяющее следующим условиям: для любых векторов х, у и любого числа k выполнены равенства

А(х + у) = А(х) + А(у), А(k×х) = k×А(х),

где запись А(х) обозначает образ х при отображении А.

Пример 12. 1). Пусть L – векторное пространство и m – фиксированное число. Каждому вектору х из L сопоставляется вектор m×x. Легко видеть, что это линейное преобразование.

2). Пусть L – пространство векторов на плоскости, тогда поворот плоскости вокруг начала координат на фиксированный угол  является линейным преобразованием.

3) Пусть L = Rⁿ  nмерное векторное пространство и А  квадратная матрица вида n´n. Каждому вектору`а из R<sup>n</sup> сопоставляется вектор А×`а. В силу свойств умножения матриц  это линейное преобразование.

Пусть L – n-мерное линейное пространство и е₁, е₂, …, е_n  его базис, А – линейное преобразование. Тогда, образ вектора х = m₁×е₁ + m₂×е₂ + …+ m_n×е_n может быть представлен в виде:

А(х) = m₁×А(е₁)+ m₂×А(е₂)+ …+ m_n×А(е_n) = . (42)

Значит, А(х) может быть найден по координатам вектора х, если известны n векторов А(е₁), А(е₂), …, А(е_n). Каждый из этих векторов тоже разложим по базису е₁, е₂, …, е_n, и пусть

А(e_j) = а_1j× е₁ + а_2j× е₂ + …+ а_nj× е_n = j = 1, 2, …, n.

Тогда равенство (42) перепишется так:

А(х) =

Отсюда, в силу единственности разложения по базису, i-ая координата вектора А(х) равна = , i = 1, 2, …, n.

Образовавшаяся здесь матрица А = (а_ij), i, j = 1, 2, …, n, называется матрицей линейного преобразования А. В этой матрице столбцы являются координатными столбцами образов базисных векторов.

Таким образом, выбор базиса в L устанавливает взаимно однозначное соответствие между линейными преобразованиями и квадратными числовыми матрицами.