Понятие меры

Определение 27 Мерой линейного ограниченного открытого множества М = (a, b) называется его длина.

m

х

es M = mes(a,b) = m(a,b) = b – a.

Определение 28. Мерой непустого ограниченного замкнутого линейного множества F = [a,b], где , называется число, равное mes F = B – A – mes ( )

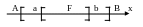
Определение 29. Иными словами, мера множества – обобщающее понятие длины, площади или объема множества в зависимости от того, какое множество рассматривается: линейное, плоское или объемное.

Примеры. Найти меру а) линейного множества А – точек интервала (ОС) оси (Ох), где О(0), С(3), b) плоского множества Х – точек квадрата АВСД, где А(2,2), В(4,2), С(4,4), Д(2,4).

Решение.

а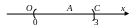 ) mes А = 3

b)

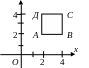
mes Х = S_АВСД = 2 · 2 = 4

Определение 30. Множества, имеющие меру, называются измеримыми.

Супремум и инфимум

Рассмотрим линейное множество.

Определение 31. Множество А называется ограниченным сверху (снизу), если существует число b такое, что для любого элемента выполняется условие: . Число b называется верхней (нижней) гранью множества.

Определение 32. Множество ограниченное и сверху и снизу называется ограниченным.

Примеры 1) ограниченного множества – (a, b), [a, b], 2) ограниченного сверху множества – (–∞, а], 3) ограниченного снизу множества – (а, ∞).

Любое ограниченное сверху (снизу) множество А имеет бесконечно много верхних (нижних) граней, образующих множество чисел, ограничивающих множество А сверху (снизу).

Пусть b – верхняя грань, тогда b^/ такое что b^/ > b, также верхняя грань.

Определение 33. Наименьшее из чисел, ограничивающих множество А сверху, называется точной верхней гранью множества А или супремумом и обозначается . Наибольшее из чисел, ограничивающих множество А снизу, называется точной нижней гранью множества А или инфимумом и обозначается

Примеры: 1) Х = (a, b), тогда = а, 2) А = (а, +∞), тогда = а, не существует.

Теорема 3. Любое непустое ограниченное сверху (снизу) числовое множество имеет точную верхнюю (нижнюю) грань.

Упорядоченные множества

 Определение 34. Множество M называется упорядоченным, если между его элементами установлено некоторое отношение a < b (a предшествует b), обладающее следующими свойствами: 1) между любыми двумя элементами a и b существует одно и только одно из трех соотношений: a = b, a < b, b < a; 2) для любых трех элементов a, b и c из a < b, b < c следует a < c.

 Пример: ) множество натуральных чисел, 2) пустое множество считается упорядоченным.

  

Замечание. Знак = мы всегда понимаем в смысле тождества, совпадения элементов. Запись a = b просто означает, что буквами a и b обозначен один и тот же элемент множества M. Поэтому из свойства 1) следует, что между двумя различными элементами выполняется одно и только одно из двух соотношений a < b или b < a.

     Если a предшествует b, то говорят, что b следует за a и пишут: b > a.

 Если в упорядоченном множестве M поменять ролями отношения < и >, т. е. вместо a < b писать a > b, и наоборот, то получится новое упорядоченное множество M', порядок которого называется обратным относительно порядка M. Например, для порядка во множестве натуральных чисел обратным будет порядок: ..., 3, 2, 1.

     Два упорядоченные множества, составленные из одних и тех же элементов, но расположенные в разном порядке, считаются различными. Поэтому при задании упорядоченного множества через его элементы необходимо указать их порядок. Будем считать, что запись слева направо соответствует порядку элементов, и сохраним прежнее обозначение фигурными скобками. Одно и то же множество можно упорядочить различным образом (если оно содержит не менее двух элементов). Так, множество натуральных чисел можно упорядочить обычным образом или в обратном порядке, можно нечетные числа поставить впереди четных или наоборот, располагая те и другие в возрастающем или убывающем порядке. Получим упорядоченные множества:

1){1, 2, 3, ...},  2){..., 3, 2, 1},  3){1, 3, 5, ..., 2, 4, 6, ...},  4){1, 3, 5, ..., 6, 4, 2}, 5){..., 5, 3, 1, 2, 4, 6, ...},   

6) {..., 5, 3, 1, ..., 6, 4, 2}.   

Замечание. Частично упорядоченное множество — понятие, которое формализует интуитивные идеи упорядочения, расположения элементов в определённой последовательности. Неформально, множество частично упорядочено, если указано, какие элементы следуют за какими (какие элементы больше каких). В общем случае может оказаться так, что некоторые пары элементов не связаны отношением «следует за». В качестве абстрактного примера можно привести совокупность подмножеств множества из трёх элементов {x,y,z} (булеан данного множества), упорядоченную по отношению включения.