Действия над множествами

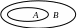
1) Подмножество:

Если может быть А = В, то пишут .

2) Объединение множеств:

Определение 6. Объединением множеств А и В называется множество или .

Свойства объединения: а) , б) = А, в) , г) если , то

3) Пересечение множеств:

Определение 7. Пересечением множеств А и В называется множество и .

Свойства пересечения: а) , б) = , в) , г) если , то

Определение 8. Два множества называются непересекающимися, если = .

4 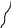) Разность множеств:

Определение 9. Разностью множеств А и В называется множество М, которое содержит все элементы А, не входящие в В: и .

Свойства разности: а) , б) .

5 ) Симметрическая разность: А В

Определение 10. Симметрической разностью множеств А и В называется множество А В

6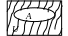 ) Если все построение происходит на некотором фиксированном множестве U, то U называют универсальным множеством. Его графически удобно изображать в виде множества точек прямоугольника.

Дополнение множества А:

Определение 11. Если , то множество элементов , но называется дополнением множества А относительно множества U и обозначается , т.е дополнением множества А называется разность .

Свойства множеств

(Доказать самостоятельно с помощью кругов Эйлера).

1. ,

2. Если и , то – транзитивность,

3. ,

4. ,

5. .

Законы алгебры множеств. Булева алгебра

Пусть А, В, С – произвольные подмножества множества F. Тогда непосредственно из определений объединения, пересечения и дополнения вытекают следующие законы:

1. – замкнутость операций объединения и пересечения,

2. , – коммутативность операций объединения и пересечения,

3. – ассоциативность операции объединения,

4. – ассоциативность операции пересечения,

5. – дистрибутивность операции пересечения относительно операции объединения,

6. – дистрибутивность операции объединения относительно операции пересечения,

7. ,

8. ,

9. ,

10. ,

11. , – законы де Моргана.

Определение 12. Если для элементов множества определены операции объединения и пересечения , для которых выполняются данные законы, то тройка называется булевой алгеброй. Таким образом, если – семейство всех частей множества F, то – булева алгебра.

Отличие алгебры чисел от алгебры множеств:

Если а и b – два числа, то между ними может быть три соотношения: a > b, a < b, a = b. Для двух множеств А и В может не выполняться ни одно из соотношений: , , А = В.

Основные определения теории множеств

Определение 13. Пусть А и В – множества. Правило f, которое каждому элементу а множества А соотносит один и только элемент b множества В, причем каждый элемент оказывается соотнесенным одному и только одному элементу , называется взаимно-однозначным соответствием между множествами А и В. Правило f – функция.

Определение 14. Число элементов конечного множества А называется мощностью множества и обозначается символом A или Card  A. (от английского cardinality - мощность).

Определение 15. Если между множествами А и В можно установить взаимнооднозначное соответствие, то множества называются эквивалентными. ~ В или что они имеют одинаковую мощность.

Замечание. Два конечных множества оказываются эквивалентными тогда и только тогда, когда они состоят из одинакового числа элементов. Так что понятие одинаковой мощности есть прямое обобщение понятия одинаковой численности конечных множеств.

Примеры эквивалентных множеств: а) А и В – множества точек на параллельных сторонах прямоугольника, б) А и В – множества точек двух концентрических окружностей.

Определение 16. Множество, эквивалентное множеству всех натуральных чисел, называется счетным.

Примеры счетных множеств: А = {1, 4, 9, 16,…, n², …}, В = .

Теорема 1. Для того, чтобы множество А было счетным, необходимо и достаточно, чтобы его можно было «перенумеровать», т.е. представить в форме последовательности: .

Определение 17. Множество всех подмножеств данного множества А называют булеаном множества и обозначают символом B(A) ( в некоторых источниках Р(А) или 2^А.

Другие названия булеана – степень множества, показательное множество, множество частей.

Ясно, что , .

Например, Пусть , тогда полный список подмножеств и, следовательно, булеан множества равен , где .

Теорема 2. Для любого конечного множества A, если мощность его Card  A = n, то мощность булеана равна Card B(A)=2ⁿ.

Пример. Пусть A = {1,2,3}. Найти количество элементов булеана и перечислить все его элементы.

Решение. B(A)={ ,{ 1 },{ 2 },{ 3},{ 1,2 },{ 1,3 },{ 2,3},{ 1,2,3 } }.

Замечание 1. Если два множества равномощны, то равномощны и их булеаны.

Замечание 2. Диагональ Кантора показывает, что булеан множества (бесконечного или нет) всегда имеет строго большую мощность, чем само множество (проще говоря, булеан должен быть 'больше', чем исходное множество). Булеан множества натуральных чисел, например, можно поставить во взаимно-однозначное соответствие с множеством вещественных чисел.

Замечание 3. Булеан множества вместе с операциями объединения, пересечения и дополнения можно рассматривать как типичный пример булевой алгебры.

Пример. Дано множество Н ={1,2,3,4,…, 10} и его подмножества А, В и С, причем , В = х – простое число}, С = х – кратно 5}. Пусть множество и В(М) – булеан этого множества. Тогда истинным будет утверждение: 1) , 2) , 3) , 4) . Решение. , , .Найдем множество , тогда множество . Истинным будет 4) утверждение.

Определение 18. Множество называется линейным, если все его элементы лежат на некотором промежутке прямой. Множество называется плоским, если все его элементы лежат в одной плоскости.

Определение 19. Пусть а – элемент линейного множества. Интервал длины 2δ с центром в точке а называется δ-окрестностью точки а: . Пусть b – элемент плоского множества, т.е. его координаты b(x₀ y₀); δ - окрестностью точки b называется внутренность любого круга радиуса δ с центром в точке b: .

Определение 20. Точка называется внутренней точкой множества, если она принадлежит ему вместе со своей окрестностью.

Определение 21. Множество называется открытым, если все его точки внутренние.

Пример: 1) (a, b), 2) R, 3) .

Определение 22. Множество называется связным, если любые две его точки можно соединить непрерывной кривой или ломаной, целиком лежащей в данном множестве.

Определение 23. Множество, состоящее из внутренних точек и обладающее свойством связности называется открытой областью или просто областью.

Примеры наипростейших областей: внутренность круга, треугольника, эллипса.

Определение 24. Точка, не принадлежащая области, называется граничной или предельной, если любая ее окрестность содержит точки, принадлежащие области.

Множество всех граничных точек – граница множества.

Определение 25. Множество, образованное областью и ее границей называется замкнутой областью. Иначе, множество называется замкнутым, если оно содержит все свои предельные точки.

Определение 26. Линейное множество называется ограниченным, если существует отрезок, внутри которого оно содержится. Плоское множество называется ограниченным, если существует круг, внутри которого оно содержится.