
- •С. Б. Волкова
- •Элементы математической статистики
- •§ 2. Планирование эксперимента
- •2.3. Оценивание функции отклика и ее параметров при ортогональном планировании.
- •2.4. Насыщенное и ненасыщенное планирование.
- •Для распределения c2 с n степенями свободы
- •Литература для дополнительного чтения
- •§ 1. Элементы математической статистики. . . . . . . . . . . 37
- •§ 2. Планирование эксперимента…………………... . . . . . 64
- •Светлана Борисовна Волкова, Юрий Николаевич Козиоров теория вероятностей
- •162600, Г. Череповец, пр. Луначарского, 5.
§ 2. Планирование эксперимента
2.1. Линейная
модель наблюдений. Пусть имеется n
наблюдений (случайных величин)
![]() ,
для которых
,
для которых
![]() ,
i
1, 2, ..., n; где
,
i
1, 2, ..., n; где
![]() – неизвестные параметры, которые
называют коэффициентами регрессии,
xij
– известные коэффициенты. Пусть X
(xij)
– матрица неизвестных коэффициентов
(порядка n p),
– неизвестные параметры, которые
называют коэффициентами регрессии,
xij
– известные коэффициенты. Пусть X
(xij)
– матрица неизвестных коэффициентов
(порядка n p),
![]() – вектор-столбец наблюдений;
– вектор-столбец наблюдений;
![]() .
Значения
.
Значения
![]() ,
минимизирующие функцию
,
минимизирующие функцию
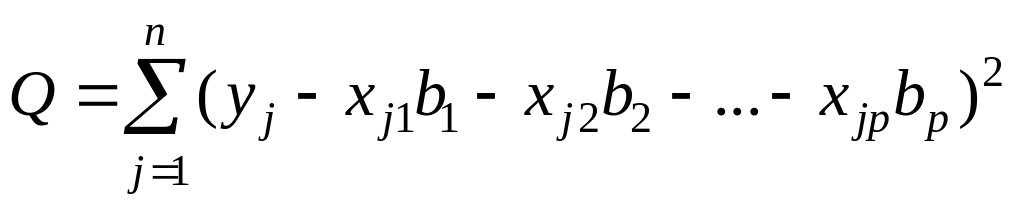 ,
,
при наблюдаемых
значениях
![]() ,
называются оценками метода наименьших
квадратов или, коротко, МНК-оценками
неизвестных параметров j.
МНК-оценки
,
называются оценками метода наименьших
квадратов или, коротко, МНК-оценками
неизвестных параметров j.
МНК-оценки
![]() параметра
параметра
![]() задаются матричным равенством:
задаются матричным равенством:
![]() .
.
Оценка
![]() параметра j
называется линейной, если fj
представляет собой линейную форму от
.
параметра j
называется линейной, если fj
представляет собой линейную форму от
.
Входные данные
заданы матрицей
![]() ,
а выходные данные заданы матрицей y.
Найти МНК-оценки неизвестных параметров
j.
,
а выходные данные заданы матрицей y.
Найти МНК-оценки неизвестных параметров
j.
386.
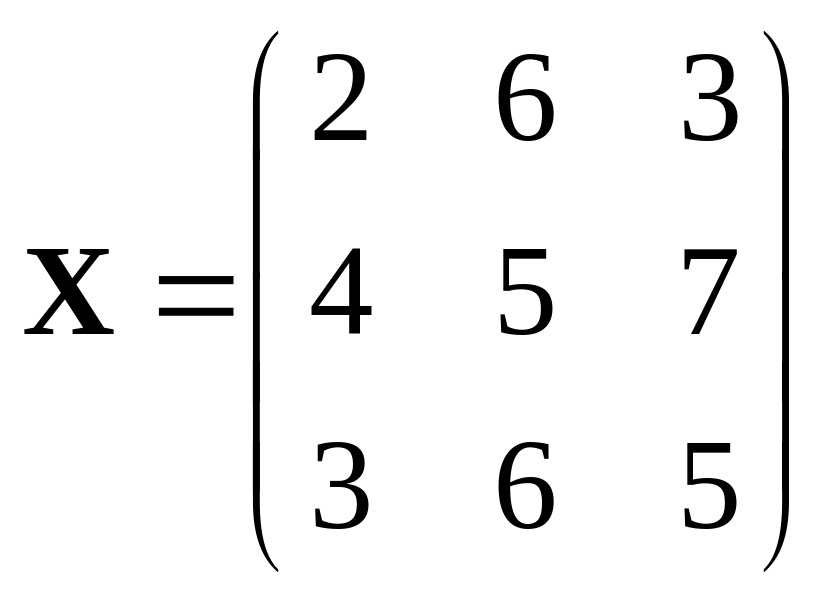 ,
,
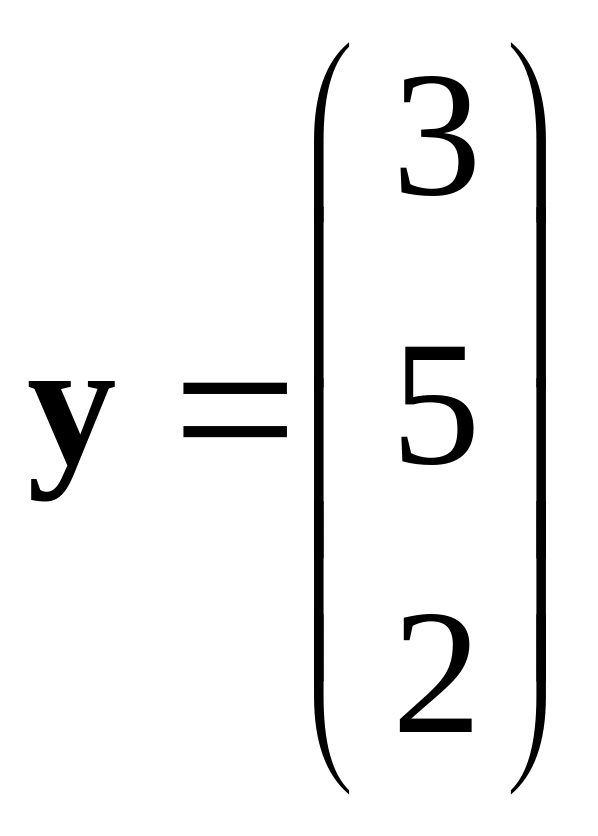 .
387.
.
387.
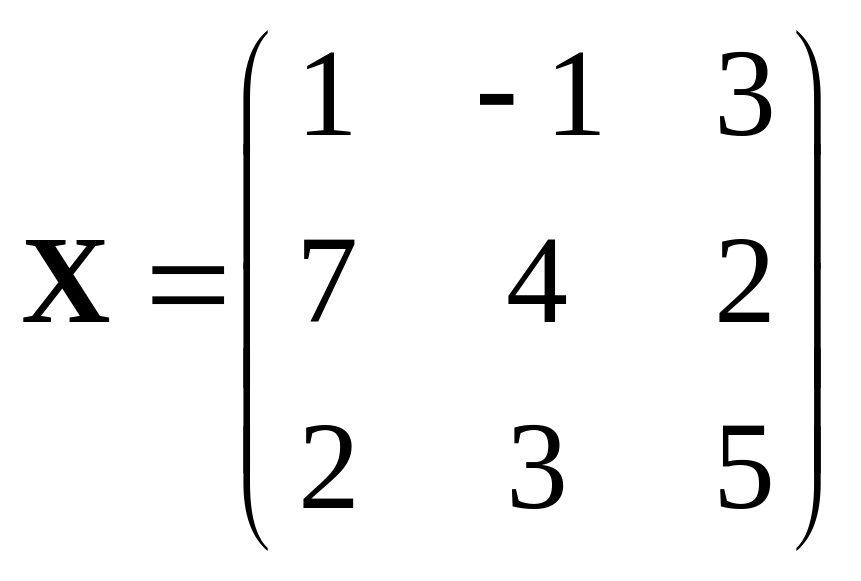 ,
,
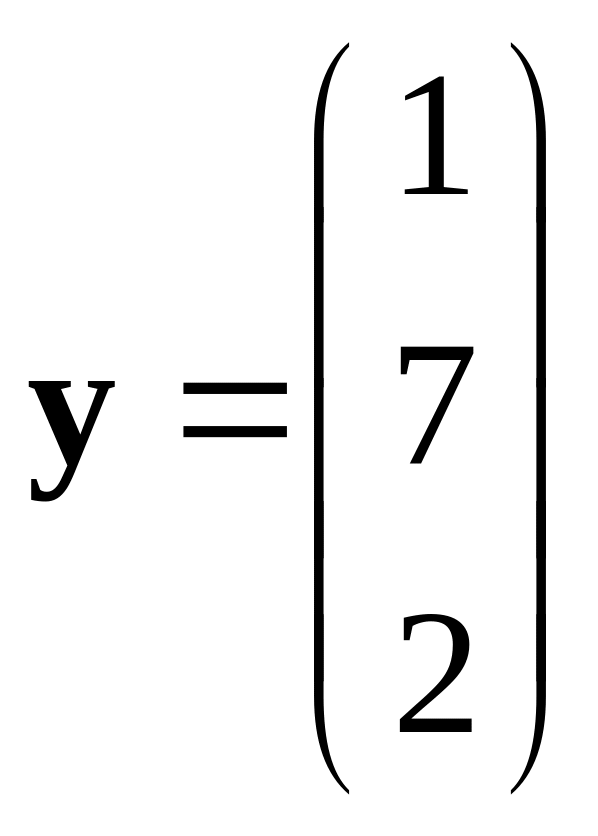 .
388.
.
388.
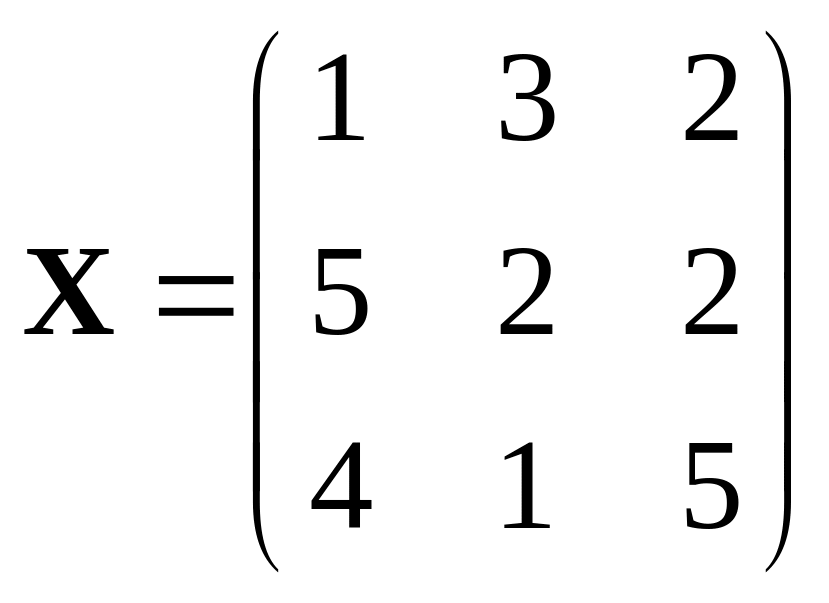 ,
,
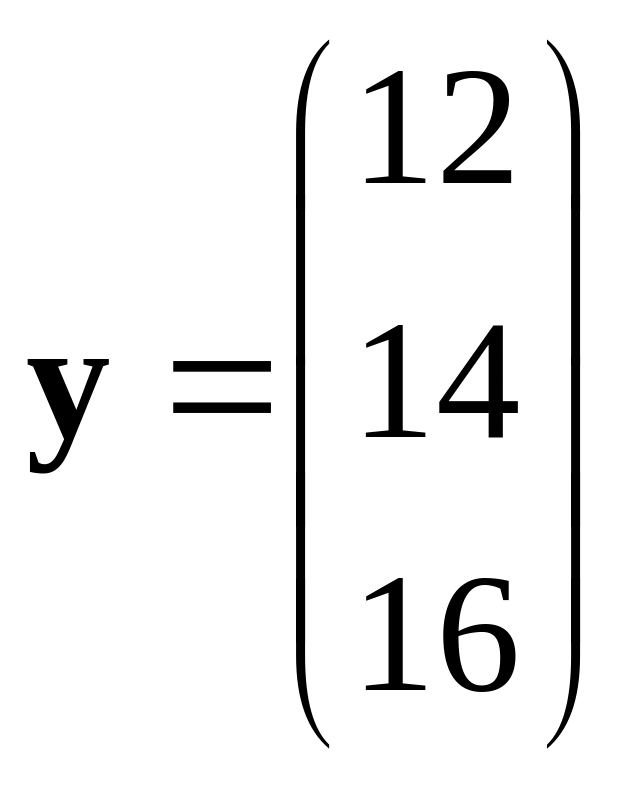 .
389.
.
389.
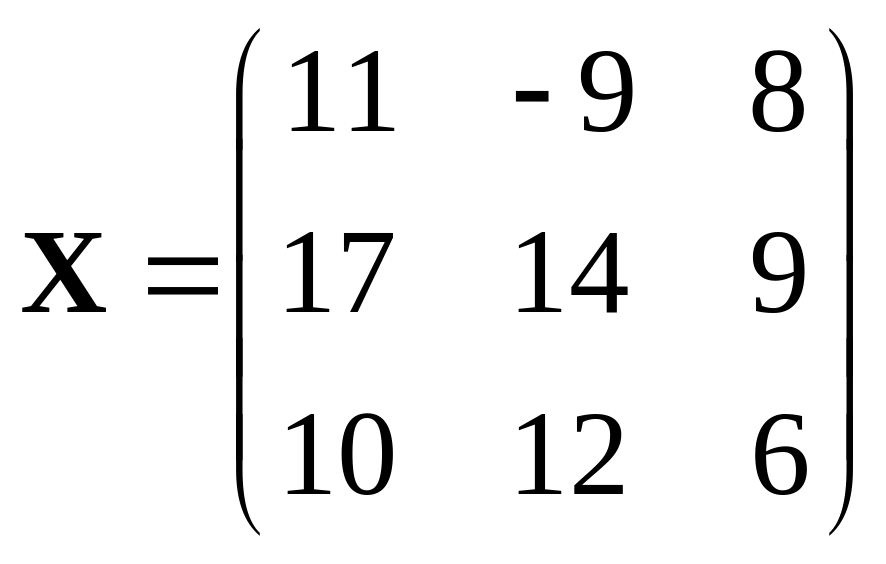 ,
,
 .
390.
.
390.
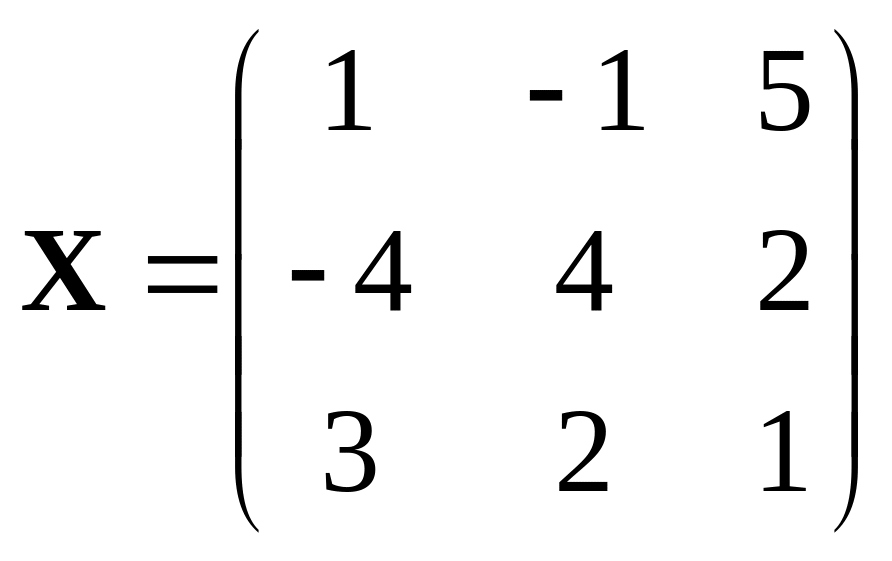 ,
,
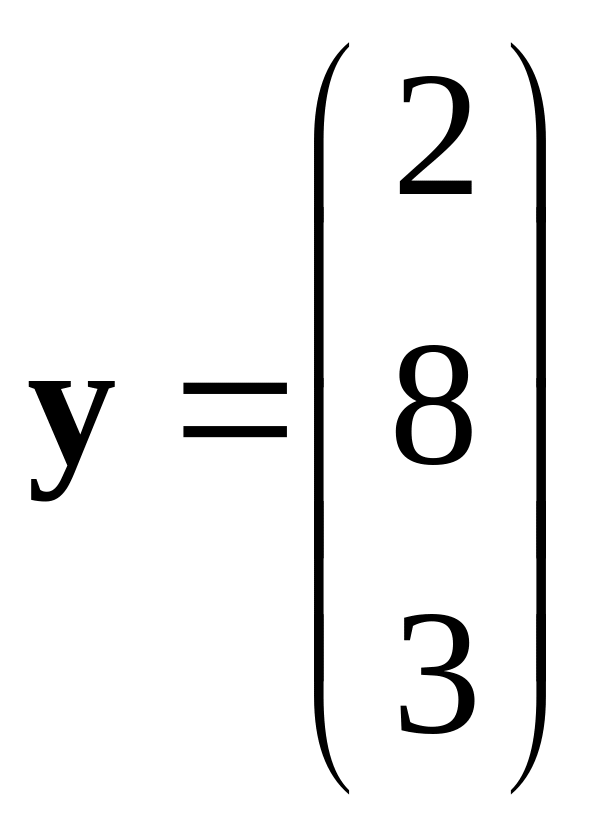 .
.
391.
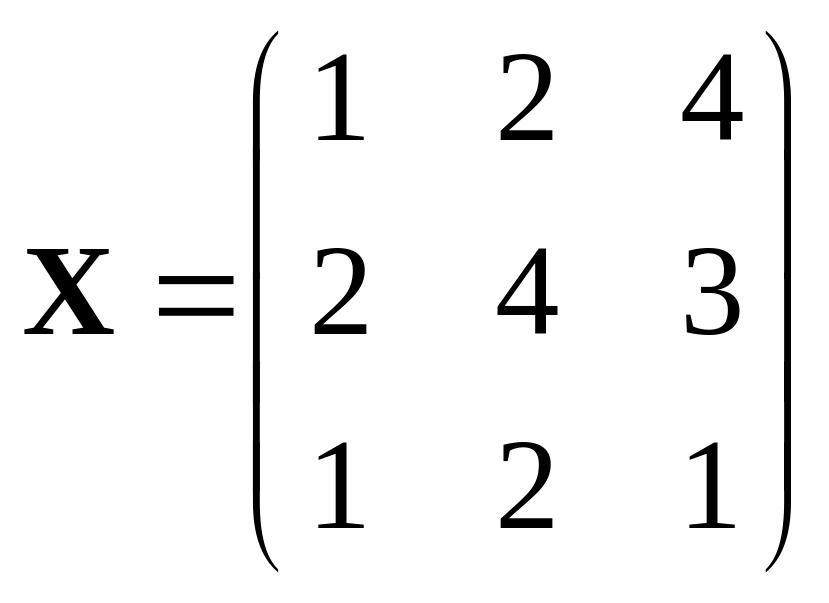 ,
,
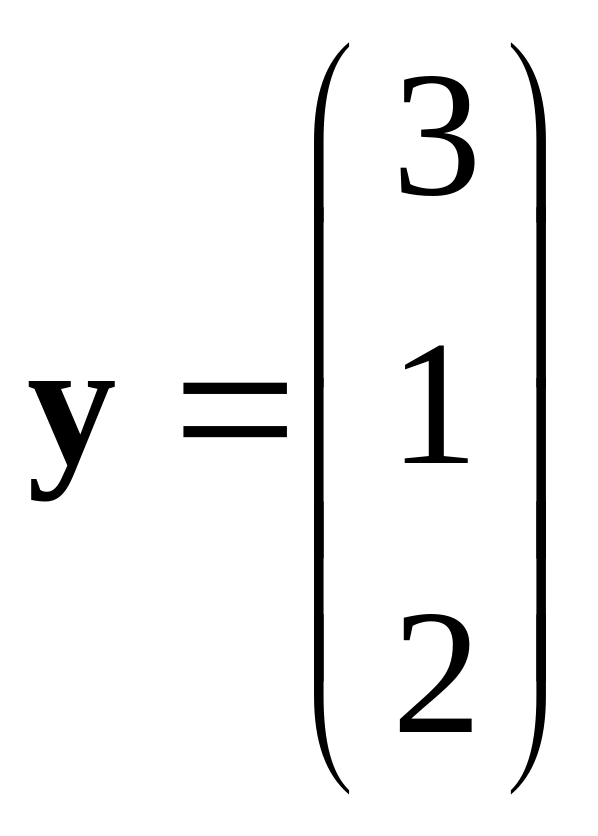 .
392.
.
392.
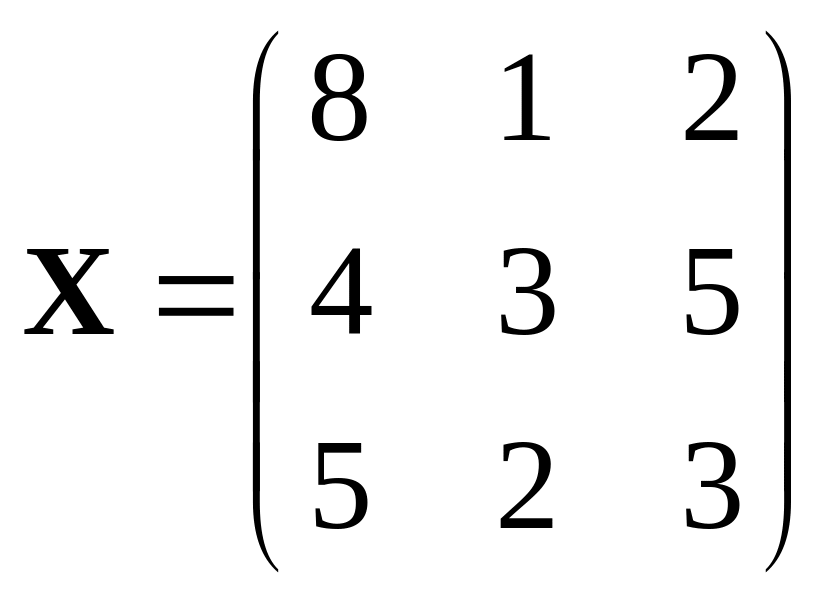 ,
,
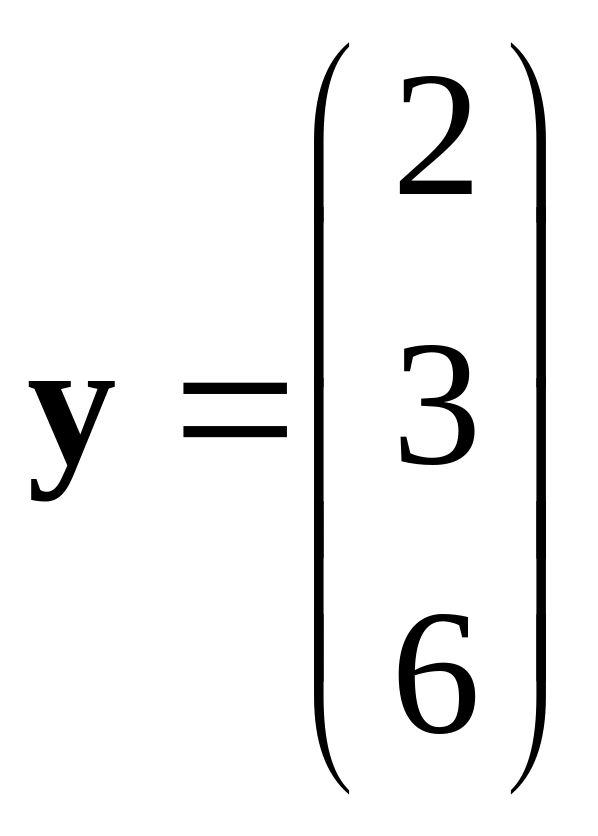 .
393.
.
393.
 ,
,
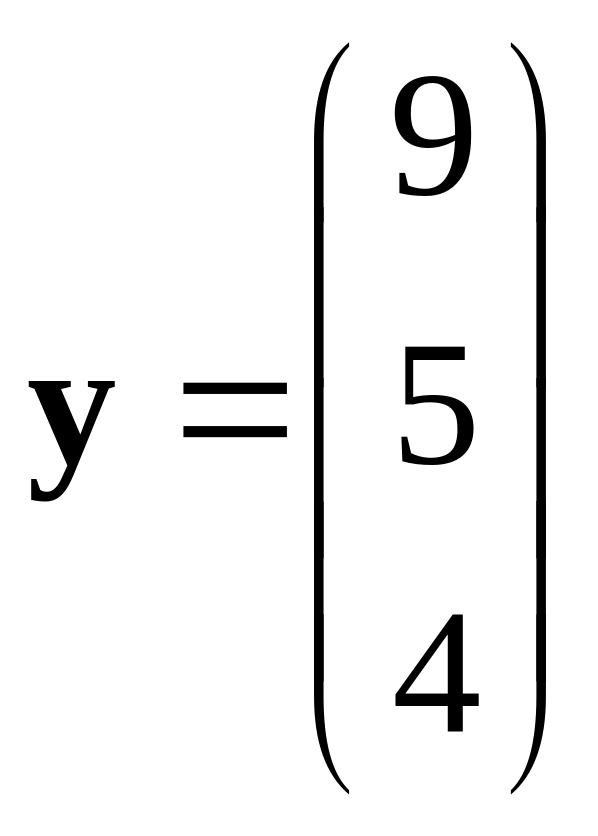 .
394
.
394
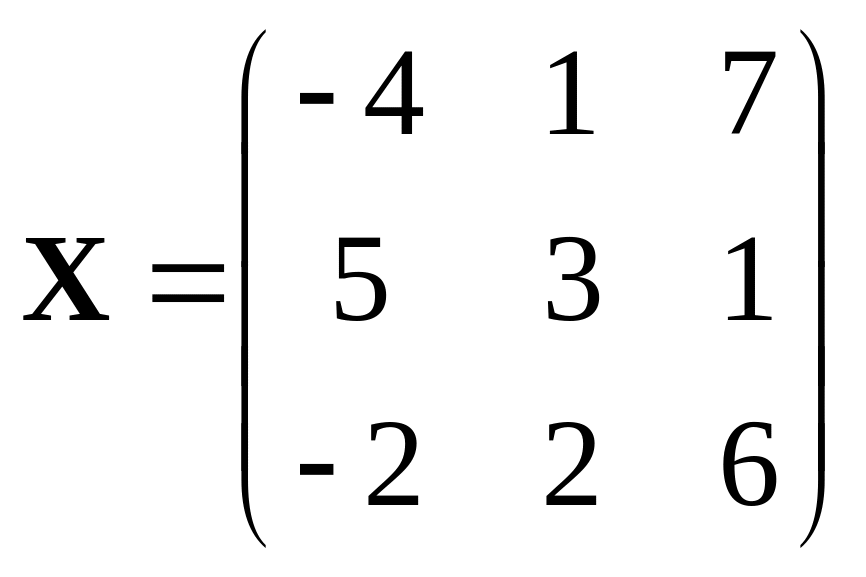 ,
,
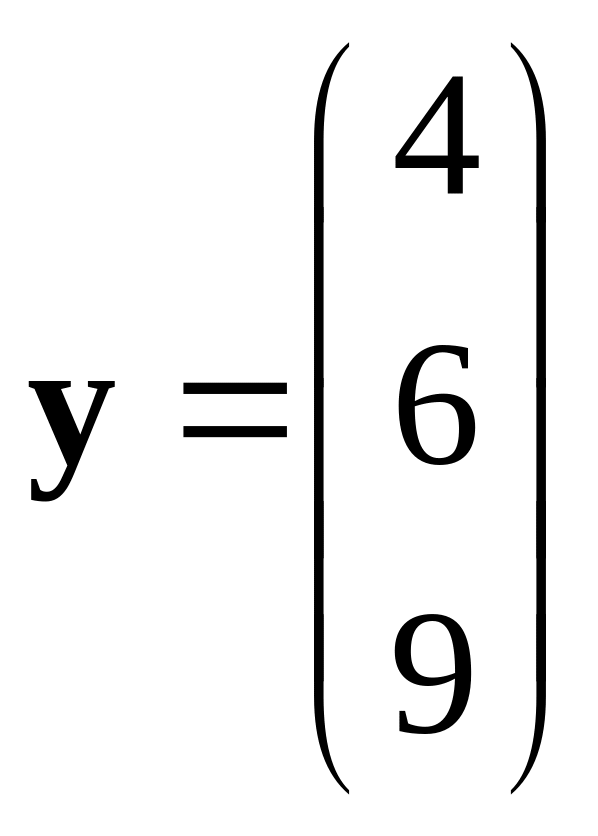 .
395.
.
395.
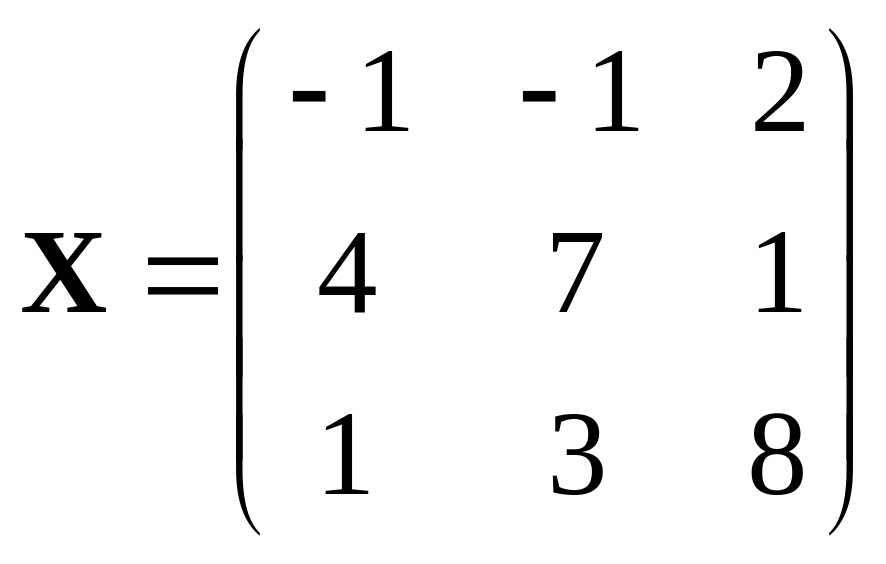 ,
,
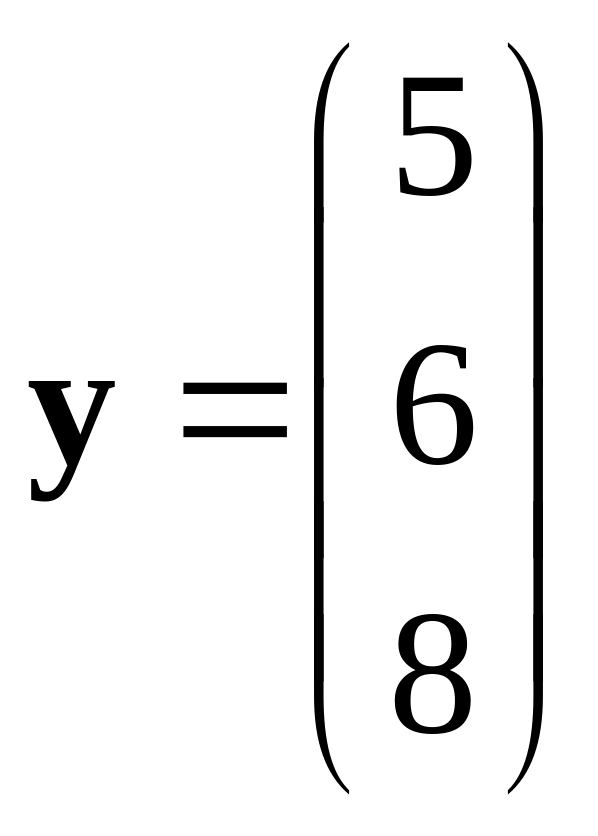 .
.
396.
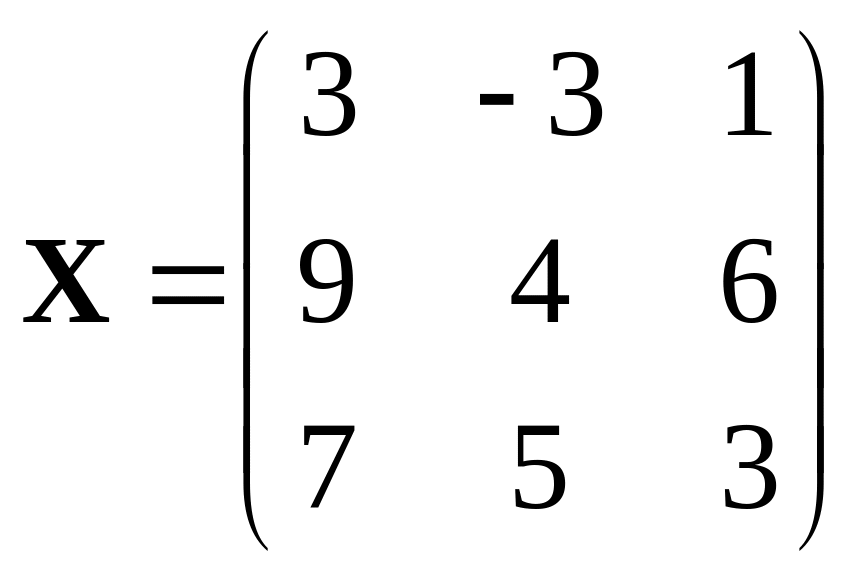 ,
,
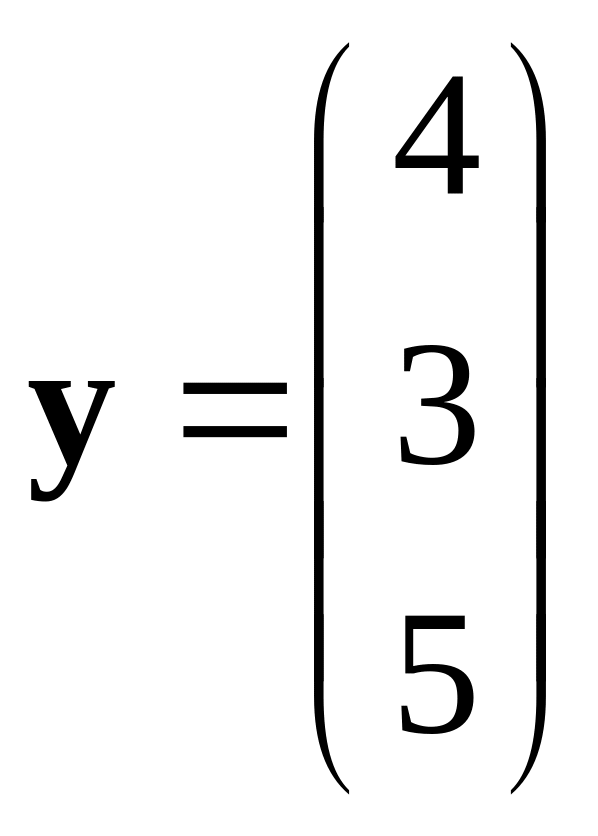 .
397.
.
397.
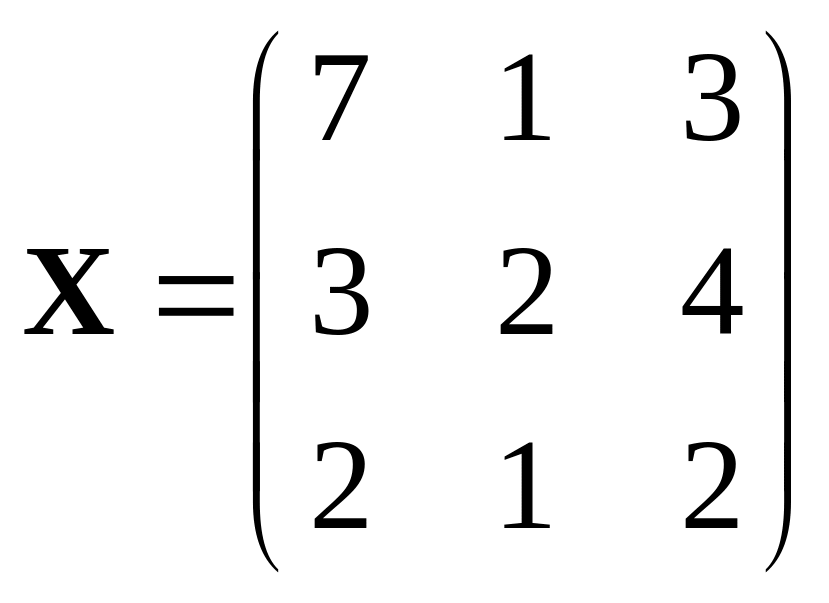 ,
,
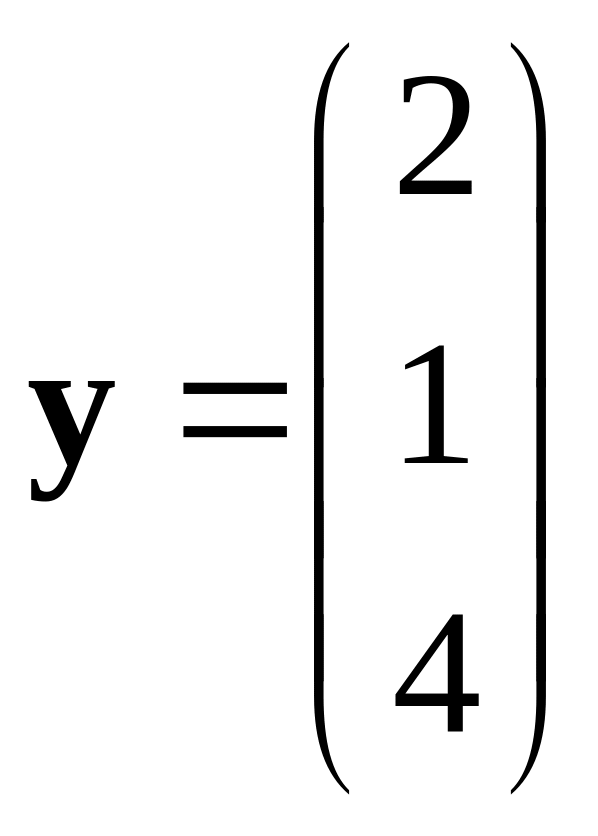 .
.
2.2. План эксперимента.
Одномерная регрессионная модель
эксперимента. Рассмотрим
![]() – эксперимент, т. е. такой эксперимент,
в котором проводится N
измерений одномерной зависимой
переменной y в
некоторых точках x
факторного пространства.
– эксперимент, т. е. такой эксперимент,
в котором проводится N
измерений одномерной зависимой
переменной y в
некоторых точках x
факторного пространства.
Набор точек xu (x1u, x2u, ..., xku) (u 1, 2, ..., N) называется планом эксперимента. Матрица
![]() (1)
(1)
называется матрицей плана эксперимента. Точки xu не обязательно все различны. Обозначим через n число различных точек плана; для определенности будем предполагать, что это точки x1, x2, ..., xn (n m N).
Среднее значение выходной переменной y, рассматриваемое как функция от вектора контролируемых переменных, называется функцией отклика. Обозначив эту функцию через , можно записать
![]() .
.
Если задана матрица плана и в точках плана, определяемых этой матрицей, проводится N наблюдений над зависимой переменной y то функция отклика задается равенством:
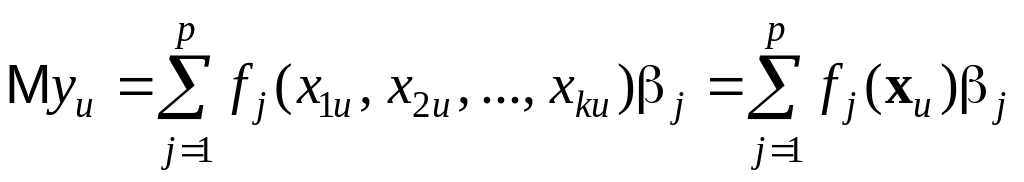 ,
(2)
,
(2)
где
![]() называются коэффициентами функции
отклика.
называются коэффициентами функции
отклика.
Матрица
![]()
называется матрицей планирования эксперимента с матрицей плана (1) и функцией отклика (2).
398. Пусть
![]() (2
4 –3 1)T –
матрица плана,
(2
4 –3 1)T –
матрица плана,
![]() – функция отклика. Тогда f0(x) 1,
f1(x) x,
f2(x) x2.
Матрица планирования имеет вид
– функция отклика. Тогда f0(x) 1,
f1(x) x,
f2(x) x2.
Матрица планирования имеет вид
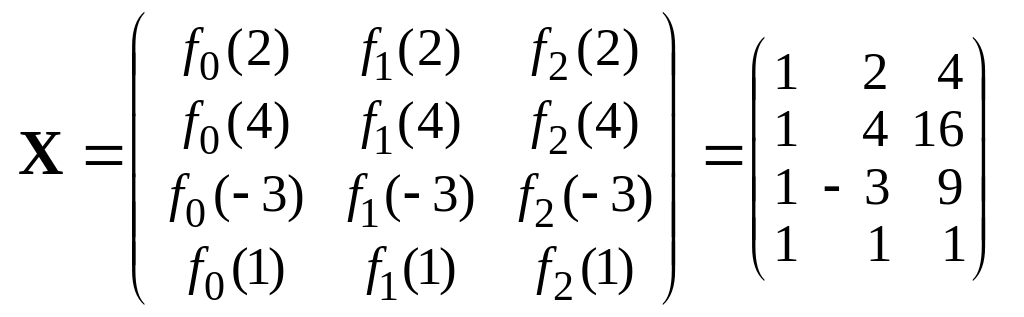 .
.
Функция отклика
имеет вид
![]() ,
,
![]() – матрица плана. Найти матрицу
планирования.
– матрица плана. Найти матрицу
планирования.
399.
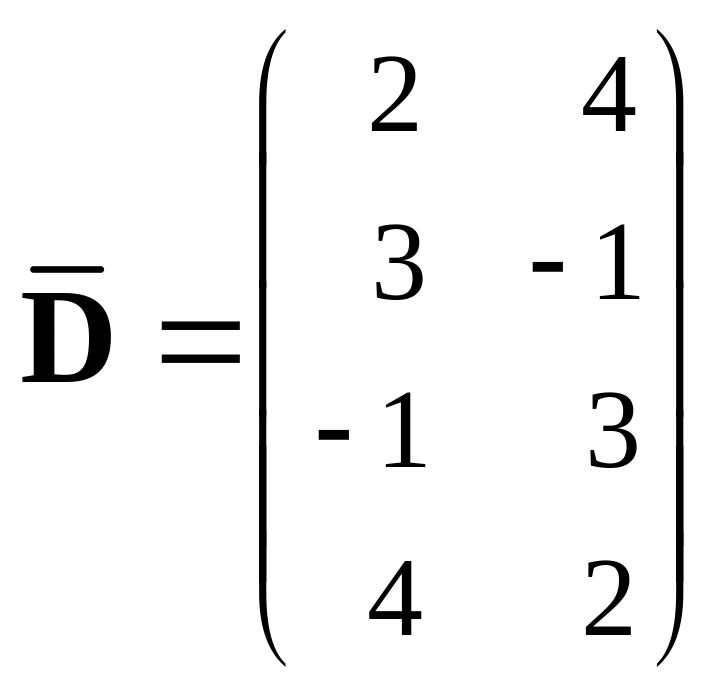 , 400.
, 400.
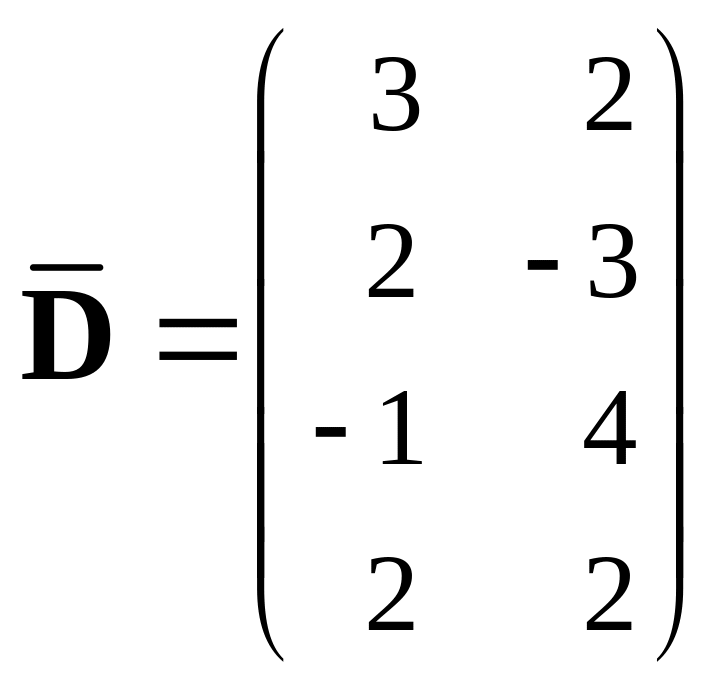 , 401.
, 401.
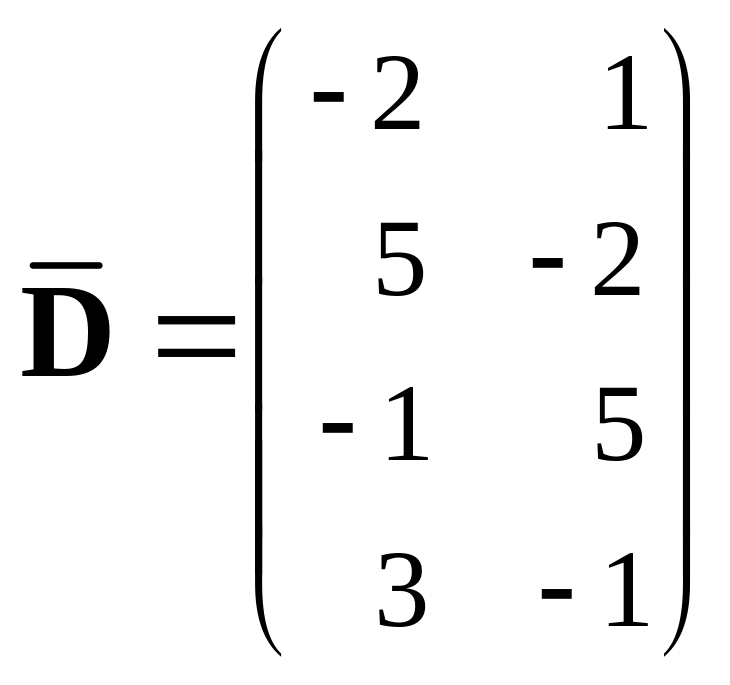 ,
,
402.
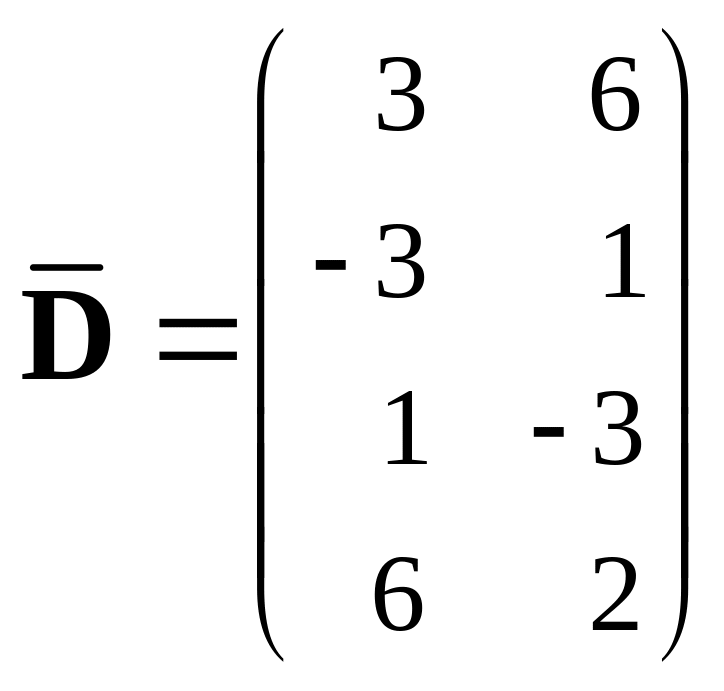 ,
403.
,
403.
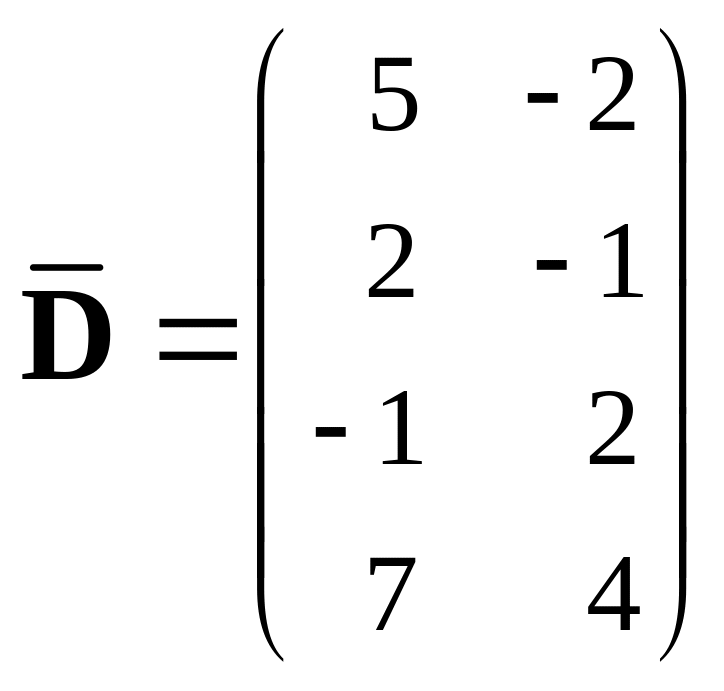 ,
404.
,
404.
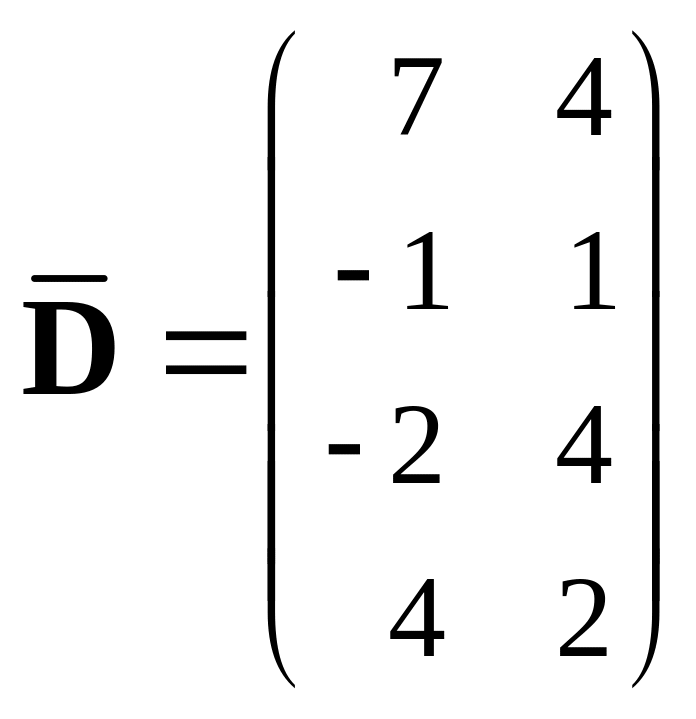 ,
,
405.
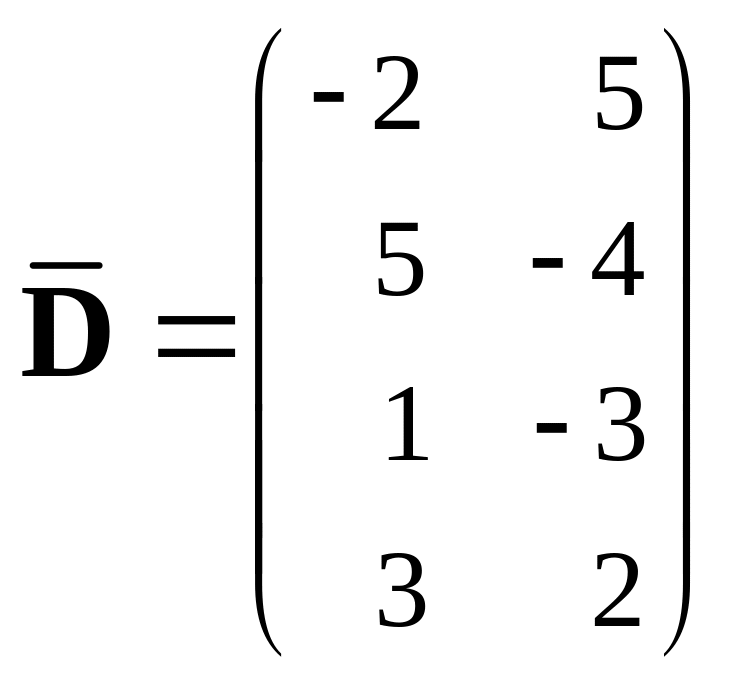 ,
406.
,
406.
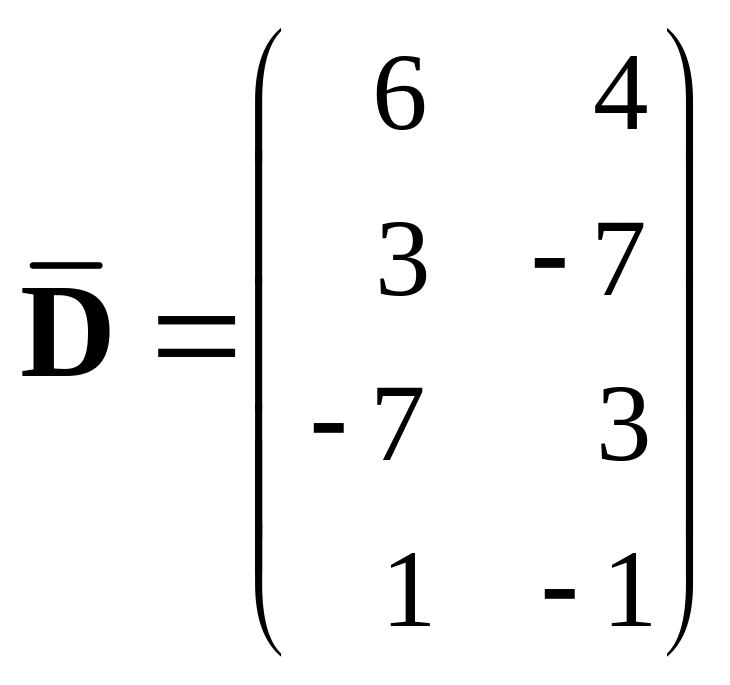 , 407.
, 407.
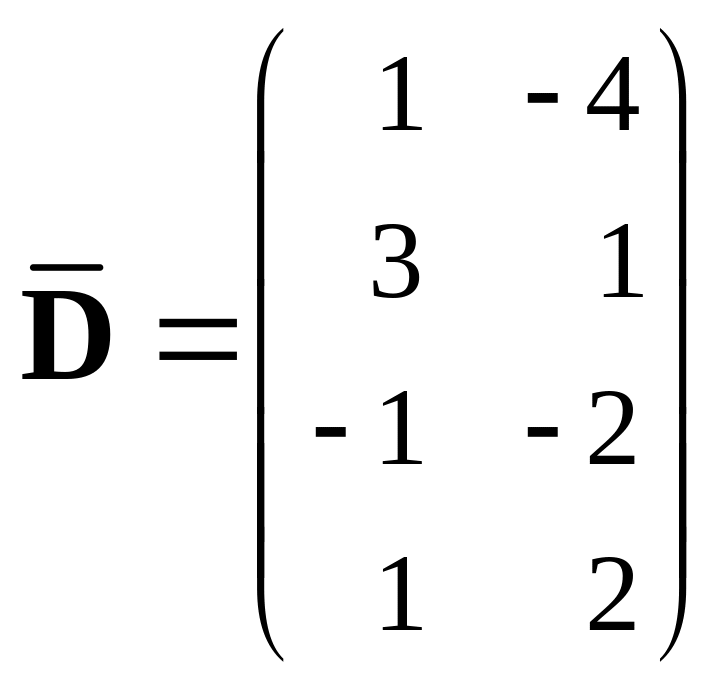 ,
,
408.
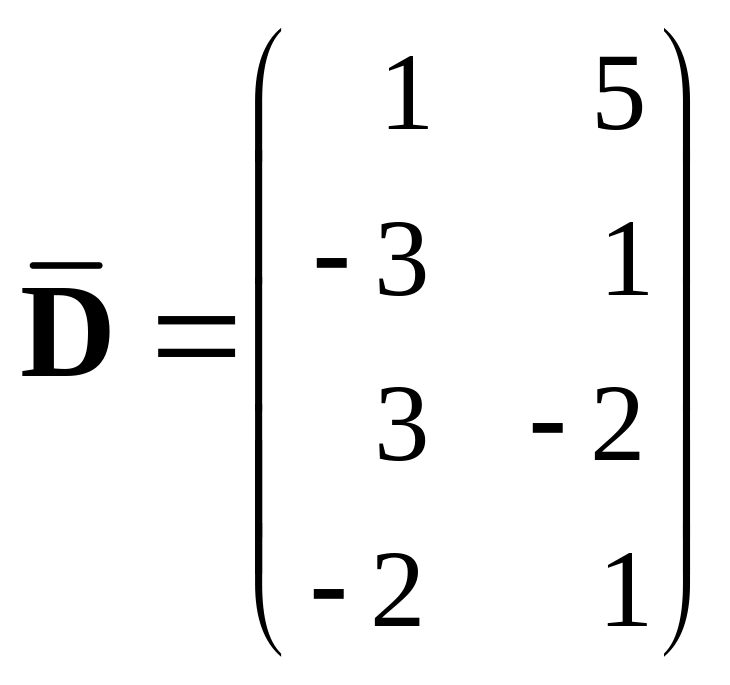 , 409.
, 409.
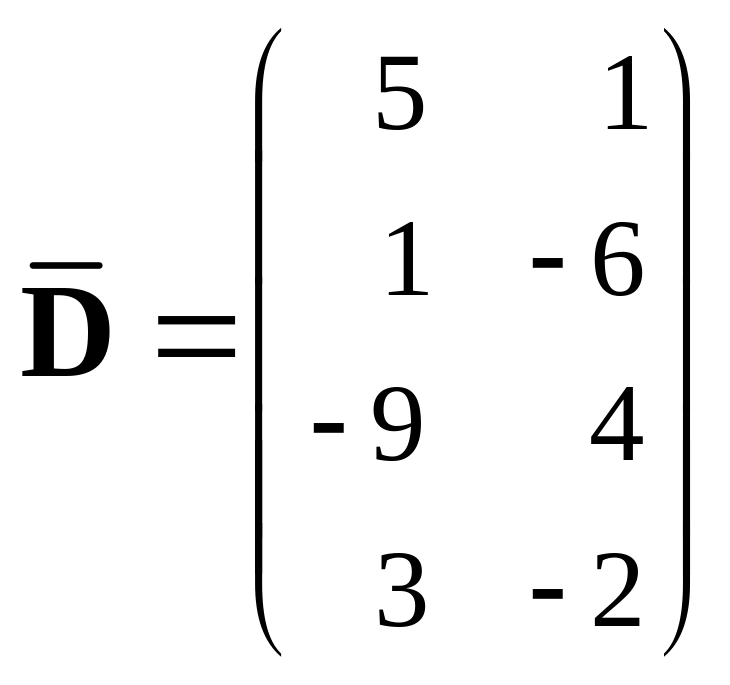 , 410.
, 410.
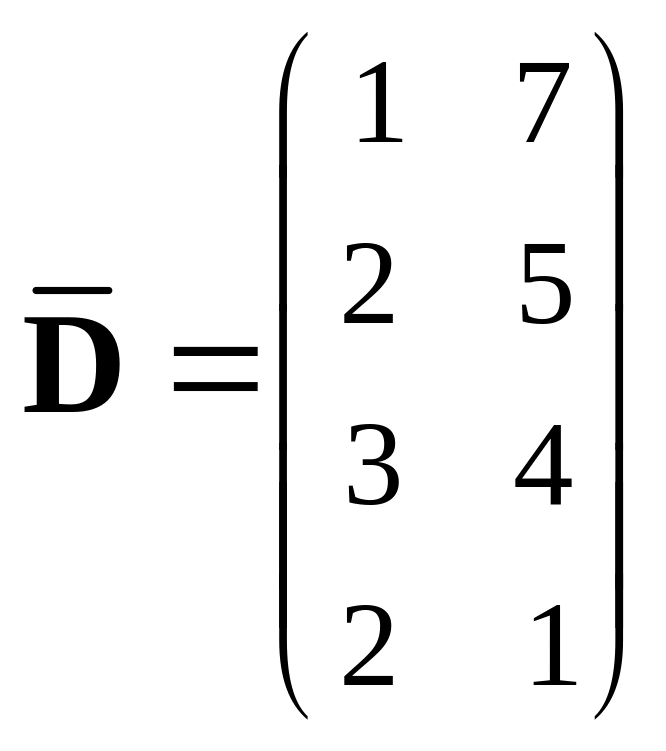 .
.
2.3. Оценивание функции отклика и ее параметров при ортогональном планировании.
Если столбцы
матрицы планирования попарно ортогональны,
т. е. при i
j (i,
j
1, 2, ..., p) выполняются
равенства fi(x1) fj(x1)
fi(x2) fj(x2)
...
fi(xN) fj(xN)
то говорят, что имеет место ортогональное
планирование. Обозначим fi(x1)2
fi(x2)2
...
fi(xN)2
| Xj
|2 , тогда при всех j
1, 2,
..., p
![]() .
.
Пусть даны функция отклика , матрица плана
и вектор-столбец y наблюдений. Найти МНК-оценки коэффициентов функции отклика.
411.
![]() ,
,
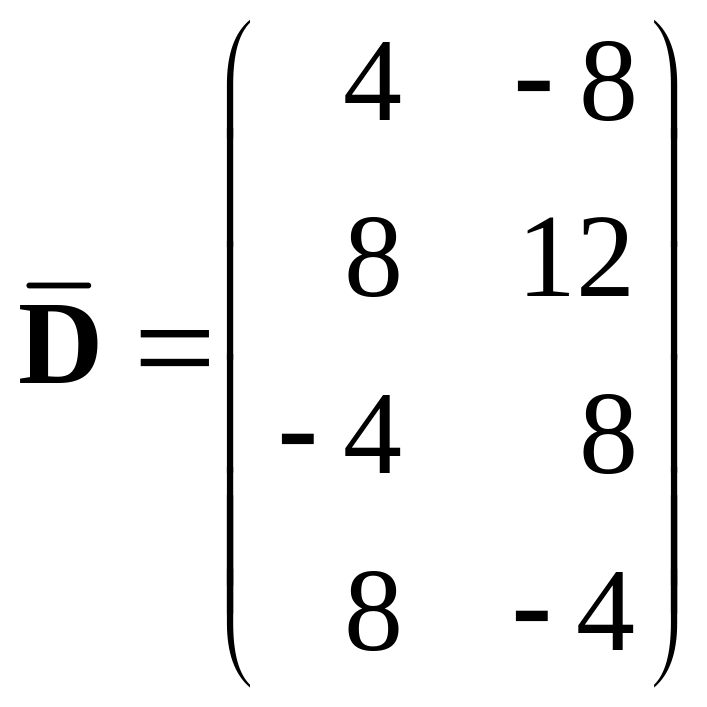 ,
,
 .
.
412.
![]() ,
,
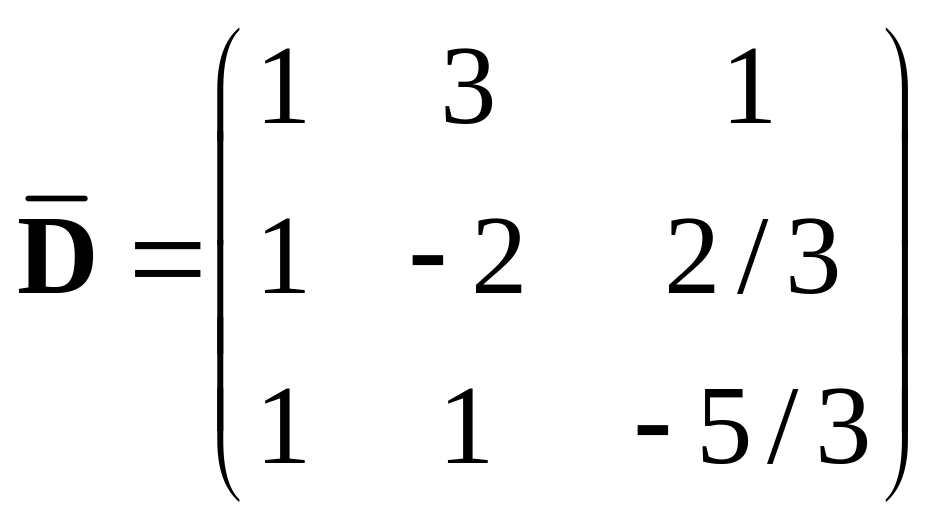 ,
,
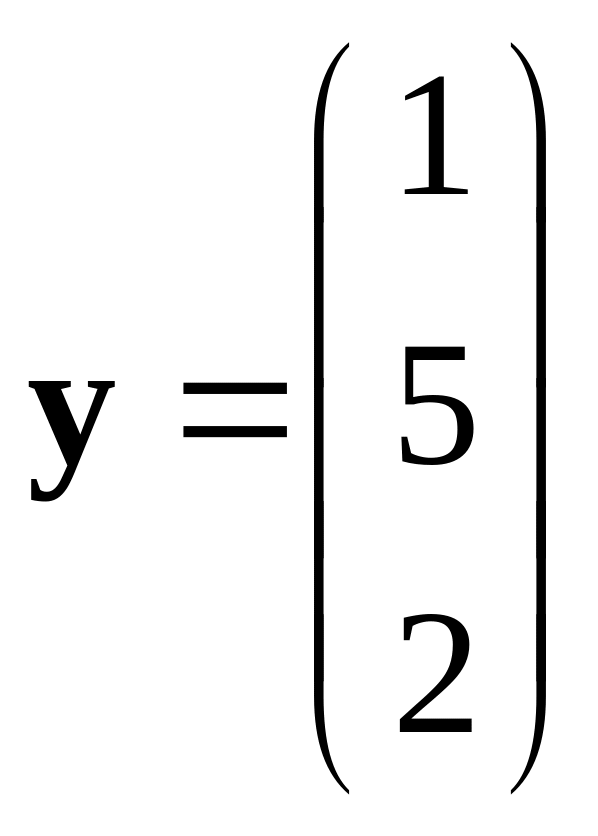 .
.
413. , , .
414. , , .
415.
,
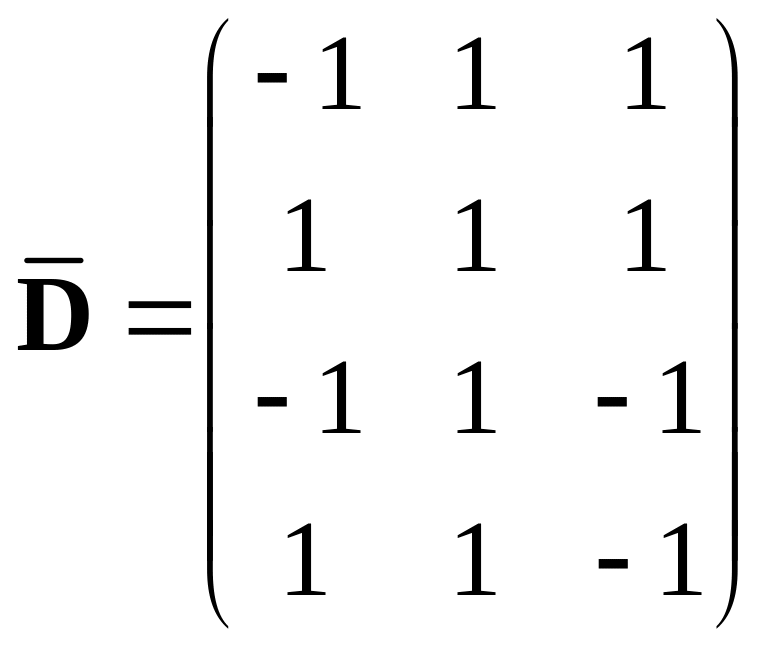 ,
,
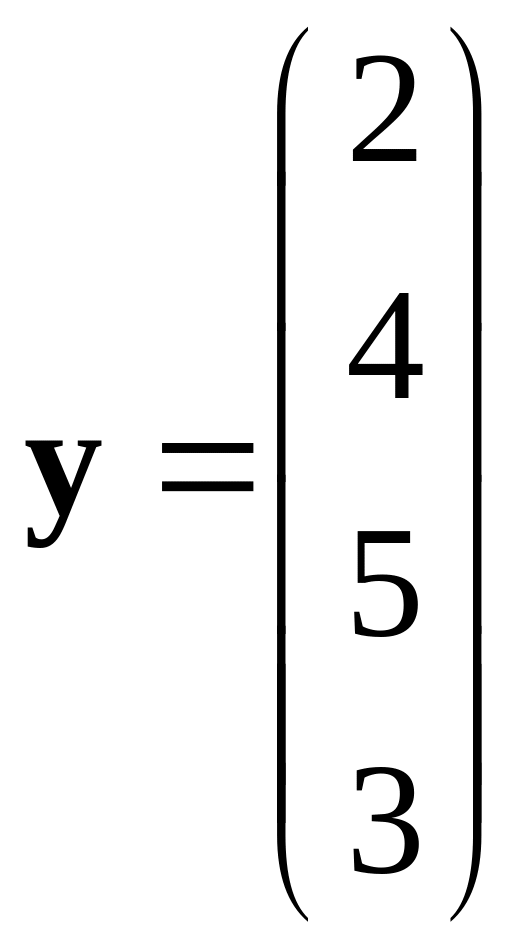 .
.
416.
,
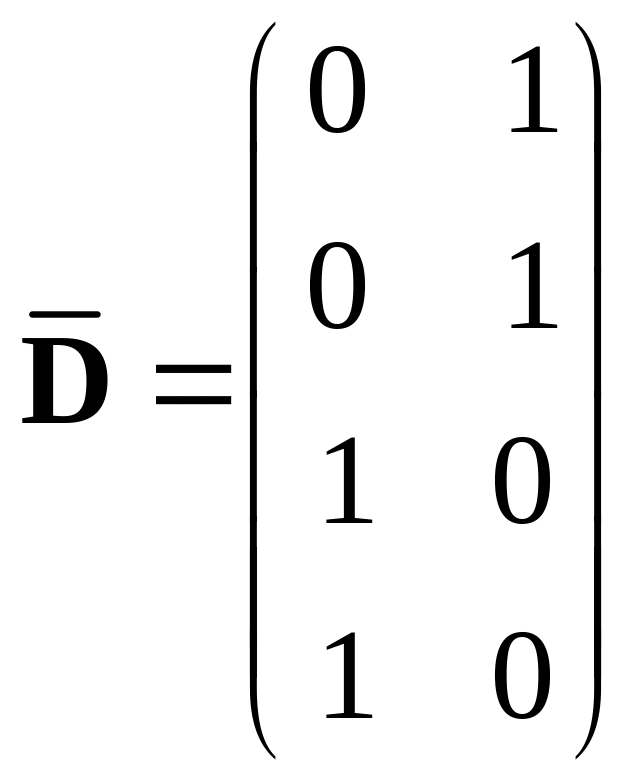 ,
,
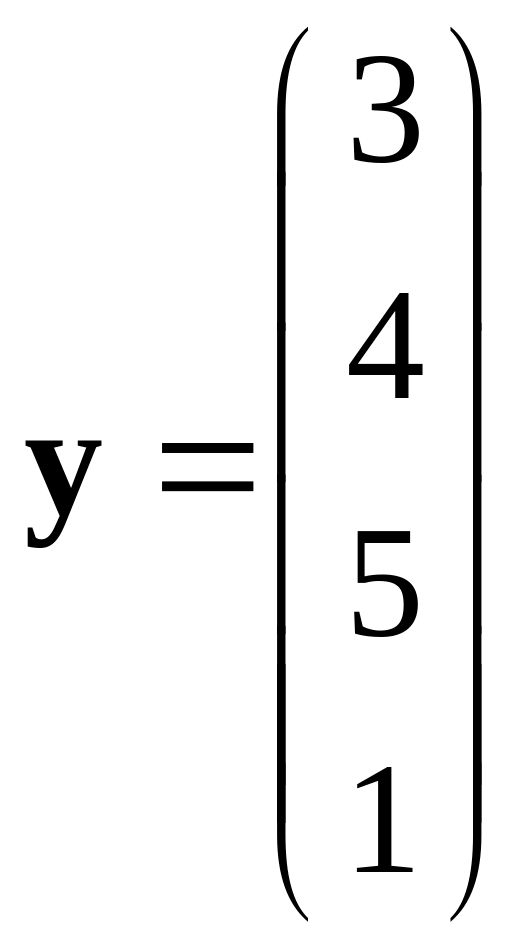 .
.
417.
,
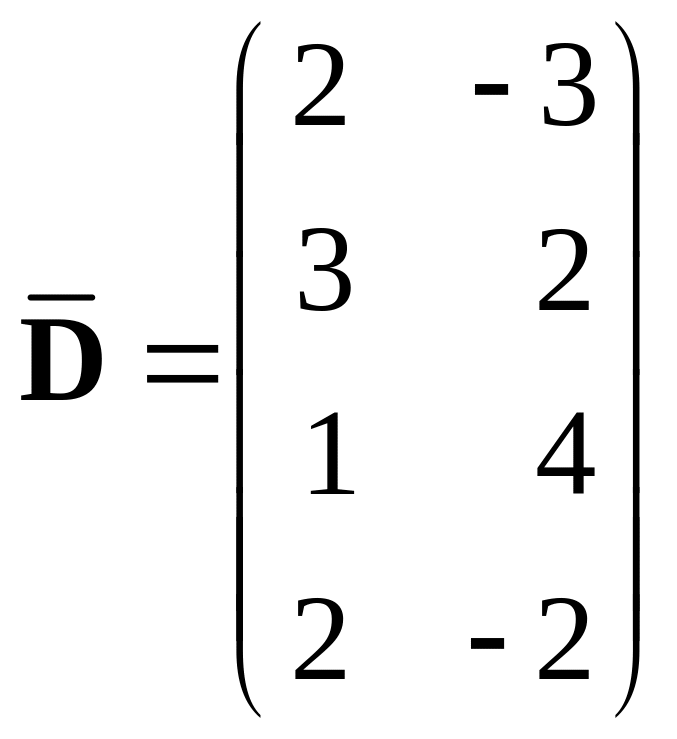 ,
,
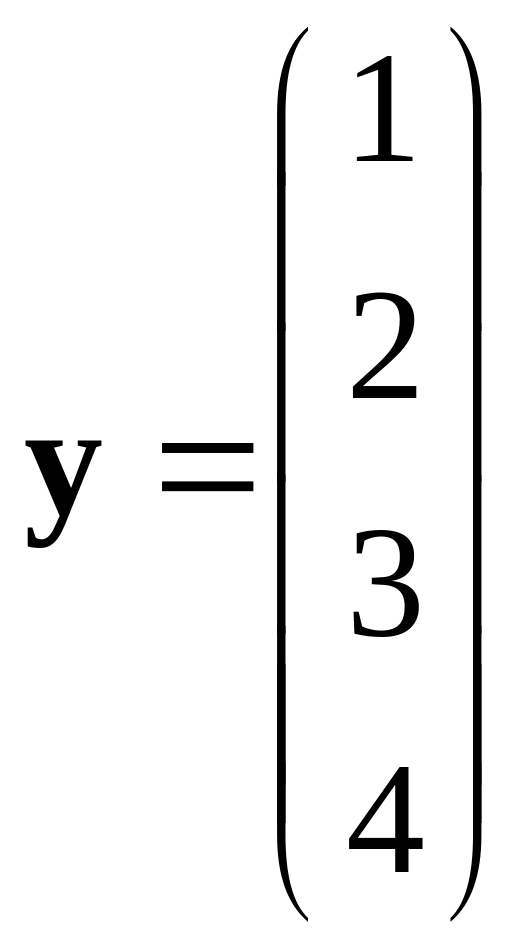 .
.
418.
,
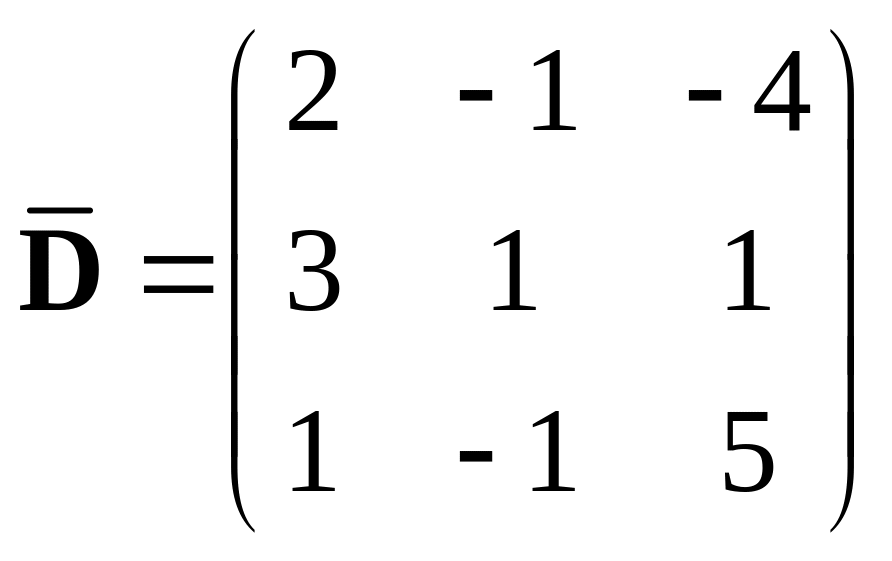 ,
,
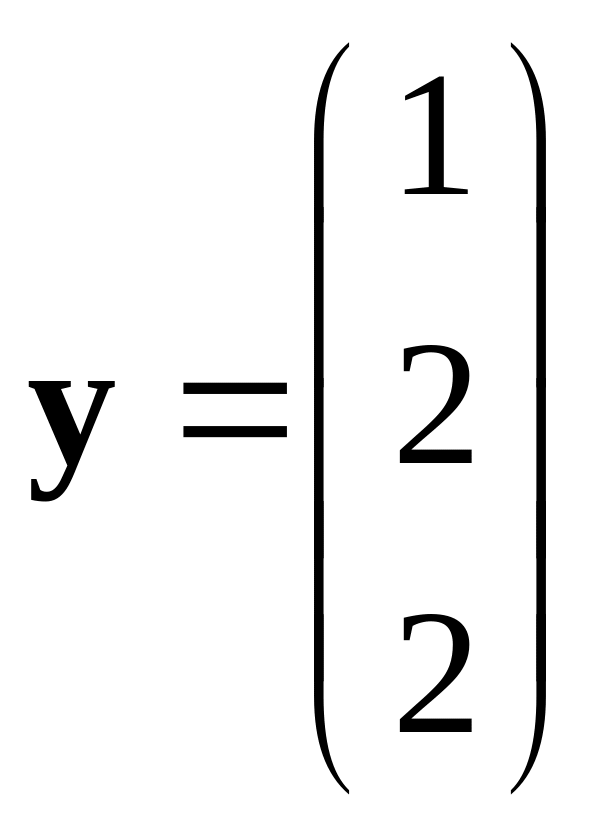 .
.
419.
,
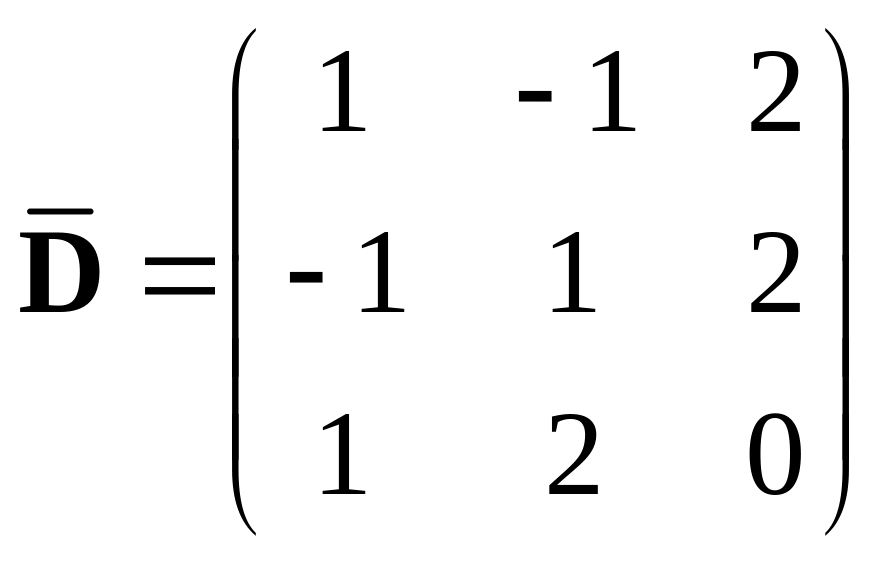 ,
,
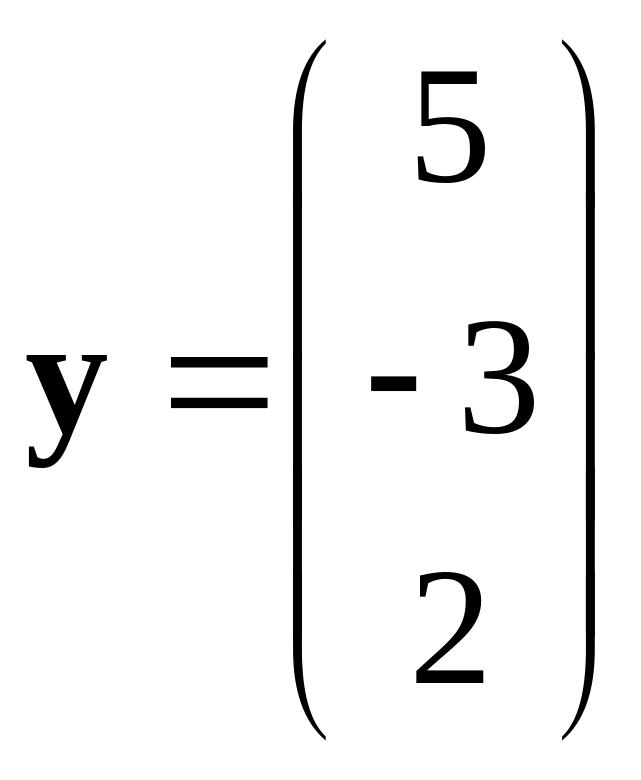 .
.
420. , , .
421.
,
,
 .
.
422. , , .
.
