Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
ГОУ ВПО «ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ»
Факультет общих математических
и естественнонаучных дисциплин
С. Б. Волкова
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ
ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
И ПЛАНИРОВАНИЮ ЭКСПЕРИМЕНТА
Череповец
2012
УДК 519 Рассмотрено на заседании ка-
федры математики, протокол №
от
Одобрено учебно-методическим
советом ГОУ ВПО ЧГУ, прото-
кол № от
Волкова С. Б Сборник задач по теории вероятностей и началам статистики: Учебное пособие. – Череповец: ГОУ ВПО ЧГУ, 2012. – 100 с.
Предлагаемое учебное пособие содержит материал для практических занятий и контрольных работ по математической статистике и планированию эксперимента и предназначено в основном для студентов, которые обучаются по направлению 270100 «Строительство», и по этой причине включает в себя значительное число задач, связанных со строительной тематикой. Приводятся основные теоретические положения и образцы решений задач. Расположение задач и упражнений соответствует содержанию учебника С. Б. Волковой “Математическая статистика и планирование эксперимента”
.
Рецензенты: .
Научный редактор: Ю. Н. Козиоров, канд. пед. наук, доцент
Ó С. Б. Волкова, 2011
Ó ГОУ ВПО «Череповецкий государственный университет», 2011
Элементы математической статистики
1.1. Первоначальная обработка статистических данных. Пусть при n-кратном повторении эксперимента получены значения x1, x2, ..., xn случайной величины . Тогда конечную последовательность (x1, x2, ..., xn) называют выборкой значений , а число n – объемом выборки. Располагая все различные элементы выборки в порядке возрастания, получим конечную последовательность (z1, z2, ..., zm), где m m n. Эту последовательность называют вариационной, а ее члены – вариантами. Если варианта zj встречалась в выборке nj раз, то число nj называют кратностью, а отношение nj / n – частотой варианты zj в полученной выборке. Т. к., сумма всех кратностей равна n, следовательно, сумма всех частот равна 1. Поэтому таблица
z1 |
z2 |
z3 |
... |
zm |
|
|
|
... |
|
задает некоторый закон распределения, который называют эмпирическим1 законом распределения для . Варианту c наибольшей частотой называют модой эмпирического распределения, число R zm – z1 размахом варьирования.
Способ наглядного изображения эмпирического закона распределения состоит в следующем: на координатной плоскости строятся точки (zj, nj / n), затем эти точки последовательно соединяются отрезками. Получается ломаная, которую называют полигоном частот. В качестве 2-й координаты вместо nj / n часто берут nj, тогда получающуюся ломаную называют полигоном кратностей.
Если kx
– количество чисел xj
в выборке, удовлетворяющих неравенству
xj < x,
то отношение kx / n
есть частота появления события ( < x),
которая является приближенным значением
вероятности этого события. Поэтому
функцию
называют эмпирической функцией
распределения для случайной величины
.
Если известно, что случайная величина имеет непрерывное распределение, то аналог ее плотности вероятностей строится следующим образом. Отрезок [z1; zm], концами которого являются наименьшая и наибольшая варианты, разбивают на частичные отрезки обычно одной и той же длины h. На j‑том частичном отрезке строится прямоугольник, высота которого равна kj / nh, где kj – количество чисел выборки, попавших в этот отрезок (если какая-либо варианта является общим концом двух соседних отрезков, то ее относят только к одному из них, обычно к правому). Фигура, составленная из построенных прямоугольников, называется гистограммой частот. Так как площадь j‑го прямоугольника равна kj / n, площадь всей фигуры равна единице.
Если объем выборки очень большой, то для ее обработки полезно использовать точечную диаграмму, которая получается следующим образом. Последовательно просматривая все числа выборки, каждое встретившееся число отмечают на координатной оси и над ним ставят точку. Если число повторяется, уже отмечено и над ним стоит точка, то над этой точкой добавляется еще одна точка. В результате над каждым отмеченным числом окажется столько точек, сколько раз это число встретилось в выборке. Таким образом, подсчитывая количество точек над каждой отмеченной вариантой, мы получим кратности вариант. Если расстояния между точками по вертикали равны 1/n (n – объем выборки), то, соединяя последовательно верхние точки отрезками, получим полигон частот.
В задачах 1 – 3 задана выборка. Требуется записать вариационную последовательность, построить таблицу для эмпирического закона распределения, найти моду и размах варьирования и построить полигон кратностей.
1. –3, 2, –1, –3, 5, –3, 2.
Решение. Выбирая различные элементы выборки и располагая их в порядке возрастания, получаем вариационную последовательность (–3, –1, 2, 5). Находя кратности и затем частоты, вариант, получаем следующую таблицу эмпирического закона распределения.
Варианты |
–3 |
–1 |
2 |
5 |
Кратности |
3 |
1 |
2 |
1 |
Частóты |
|
|
|
|
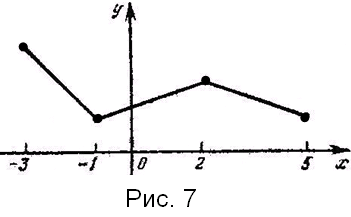
Мода распределения равна –3, размах варьирования R 5 – (–3) 8. Построив точки (zj, kj), где z1 –3, k1 3; z2 –1, k2 1; z3 2, k3 2; z4 5, k4 1, и последовательно соединив их отрезками, получаем полигон кратностей (рис. 7).
2. 0; 0,5; 0,2; 0; 0,8; 0; 0,5. 3. 13, 8, 11, 13, 5, 13, 8.
4. Изготовлена партия шариков диаметра 2 мм. Для контроля взяли 200 шариков и измерили их диаметр. Получили следующие результаты.
Диаметр (мм) |
1,97 |
1,98 |
1,99 |
2,00 |
2,01 |
2,02 |
2,03 |
Количество |
20 |
20 |
40 |
50 |
40 |
20 |
10 |
Требуется найти эмпирическую функцию распределения, диаметров и построить ее график.
Решение. Имеем
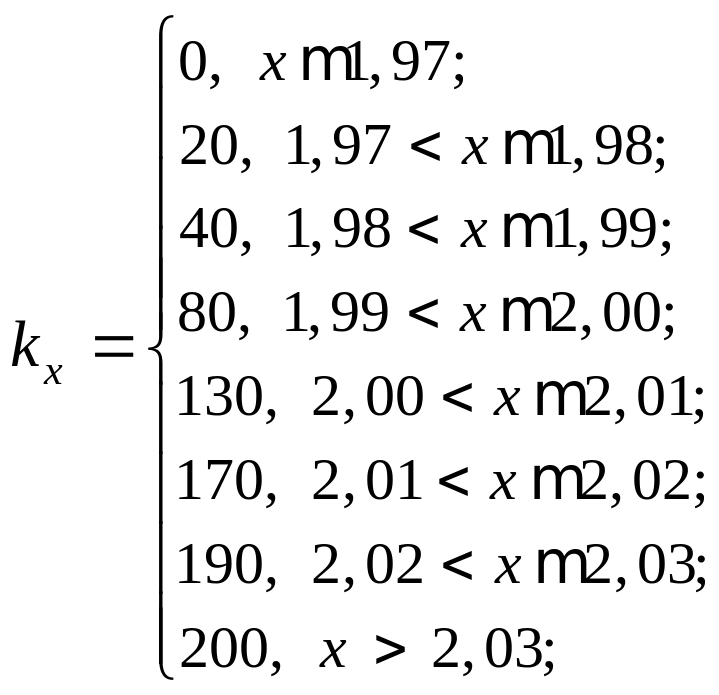
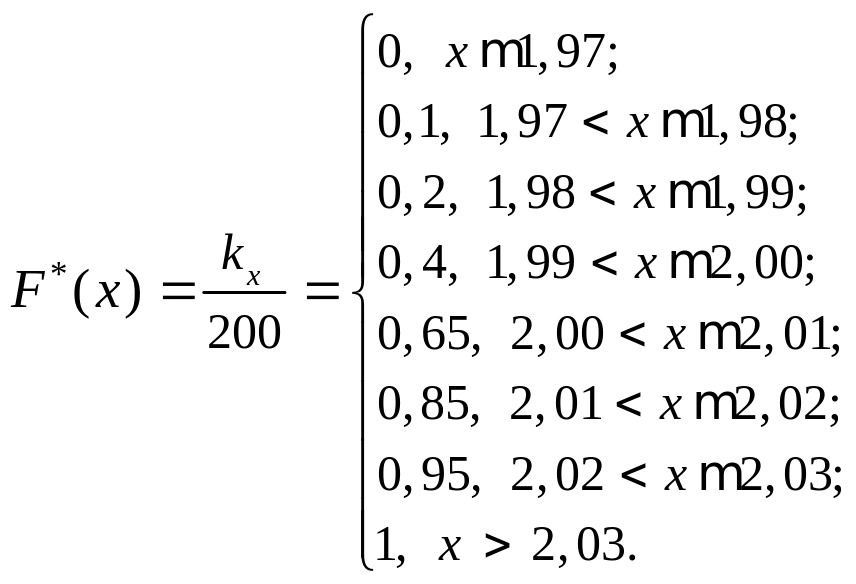
График функции F * изображен на рис. 8.
5. Построить гистограмму частот из четырех столбцов, используя следующие результаты наблюдений.
Варианты |
– 2 |
0 |
1 |
2 |
3 |
5 |
7 |
Количество в выборке |
4 |
5 |
7 |
8 |
6 |
2 |
1 |
Р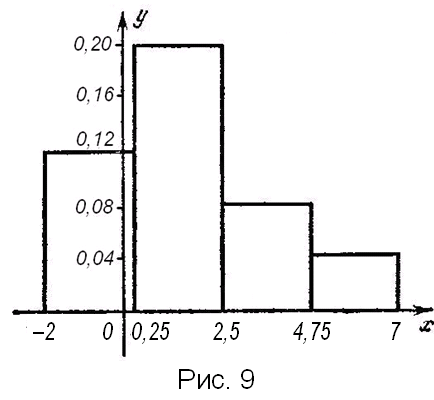
ешение.
Здесь n 33,
наименьшая и наибольшая варианты –2 и
7, длина отрезка [– 2; 7] равна 9. Разобьем
этот отрезок на 4 отрезка длины h 9 : 4
2,25.
Подсчитаем количество чисел выборки
в каждом отрезке и высоту столбцов.
Отрезок |
kj |
kj /nh |
[–2; 0,25] |
9 |
0,12 |
[0,25; 2,5] |
15 |
0,20 |
[2,5; 4,75] |
6 |
0,08 |
[4,75; 7] |
3 |
0,04 |
Гистограмма приведена на рис. 9.
6. Дана выборка объема n 100 значений случайной величины . Требуется: 1) построить точечную диаграмму и полигон частот; 2) составить таблицу эмпирического закона распределения для .
7,31; 7,24; 7,35; 7,32; 7,36; 7,40; 7,27; 7,36; 7,28; 7,37;
7,34; 7,36; 7,43; 7,36; 7,34; 7,36; 7,37; 7,32; 7,33; 7,38;
7,33; 7,34; 7,37; 7,33; 7,34; 7,38; 7,36; 7,29; 7,36; 7,34;
7,27; 7,36; 7,35; 7,29; 7,32; 7,42; 7,35; 7,35; 7,37; 7,31;
7,36; 7,32; 7,35; 7,37; 7,35; 7,38; 7,28; 7,39; 7,34; 7,35;
7,28; 7,34; 7,38; 7,40; 7,36; 7,34; 7,37; 7,33; 7,33; 7,29;
7,32; 7,38; 7,31; 7,38; 7,33; 7,35; 7,39; 7,34; 7,40; 7,35;
7,37; 7,42; 7,38; 7,35; 7,33; 7,28; 7,31; 7,36; 7,32; 7,35;
7,34; 7,33; 7,39; 7,33; 7,35; 7,33; 7,34; 7,35; 7,34; 7,35;
7,31; 7,36; 7,29; 7,34; 7,40; 7,37; 7,31; 7,39; 7,35; 7,32.
Решение.
1) Отмечаем и подписываем последовательно
на оси абсцисс точки 7,31; 7,24; 7,35; 7,32; 7,36;
7,40; 7,27, выставляя над ними точки на
расстоянии
единицы масштаба от оси абсцисс. Следующее
число таблицы 7,36 уже встречалось, ставим
точку том же расстоянии 0,01 над предыдущей
точкой. Продолжая этот процесс до
исчерпания всех чисел таблицы, получаем
точечную диаграмму, изображенную на
рис. 10. Верхние точки имеют координаты
zj,
nj / n,
где zj
– j-я
варианта, а nj
– количество точек над вариантой zj.
Поэтому, соединяя последовательно
верхние точки отрезками, получаем
полигон частот,
2) Подсчитывая количество точек над каждой вариантой, получаем кратности вариант, деля их на n 100, получаем частóты вариант и эмпирический закон распределения (табл. на стр. 70).
В задачах 7 – 50 дана выборка объема n 100. Требуется: 1) построить точечную диаграмму и полигон частот; 2) составить таблицу эмпирического закона распределения; 3) найти эмпирическую функцию распределения и построить ее график; 4) построить гистограмму (число столбцов выбрать любое в пределах от 5 до 7).
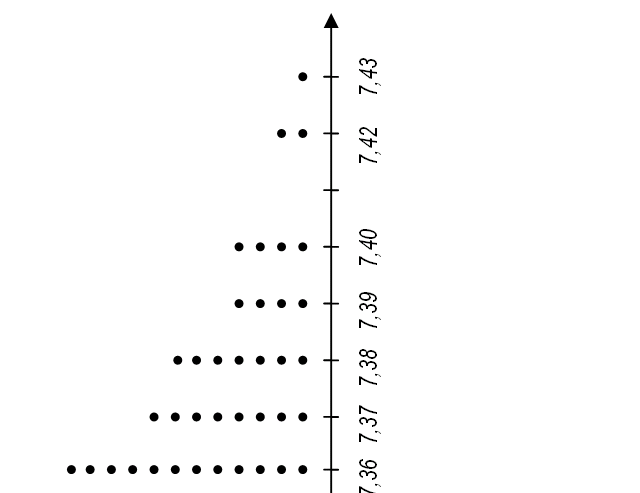
Рис. 10 |
7,43 |
1 |
0,01 |
7,42 |
2 |
0,02 |
|
7,40 |
4 |
0,04 |
|
7,39 |
4 |
0,04 |
|
7,38 |
7 |
0,07 |
|
7,37 |
8 |
0,08 |
|
7,36 |
12 |
0,12 |
|
7,35 |
15 |
0,15 |
|
7,34 |
13 |
0,13 |
|
7,33 |
10 |
0,10 |
|
7,32 |
7 |
0,07 |
|
7,31 |
6 |
0,06 |
|
7,29 |
4 |
0,04 |
|
7,28 |
4 |
0,04 |
|
7,27 |
2 |
0,02 |
|
7,24 |
1 |
0,01 |
7. |
12 |
12 |
4 |
14 |
17 |
12 |
12 |
10 |
16 |
11 |
12 |
6 |
14 |
17 |
14 |
|
13 |
15 |
10 |
12 |
15 |
13 |
14 |
15 |
16 |
11 |
9 |
19 |
15 |
11 |
11 |
11 |
15 |
15 |
15 |
8 |
9 |
15 |
13 |
16 |
0 |
5 |
13 |
11 |
9 |
13 |
11 |
12 |
13 |
10 |
11 |
14 |
12 |
14 |
15 |
7 |
19 |
14 |
12 |
12 |
6 |
13 |
6 |
15 |
13 |
11 |
13 |
16 |
17 |
13 |
6 |
11 |
7 |
15 |
10 |
5 |
11 |
7 |
14 |
3 |
12 |
9 |
16 |
12 |
15 |
13 |
11 |
16 |
8 |
14 |
15 |
17 |
15 |
14 |
16 |
14 |
17 |
16 |
14 |
10 |
12 |
8. |
13 |
15 |
14 |
12 |
14 |
14 |
16 |
12 |
3 |
15 |
10 |
6 |
9 |
16 |
16 |
|
12 |
16 |
15 |
17 |
10 |
15 |
13 |
10 |
10 |
15 |
14 |
16 |
10 |
5 |
14 |
15 |
14 |
15 |
12 |
13 |
15 |
15 |
14 |
15 |
15 |
10 |
10 |
13 |
11 |
15 |
13 |
13 |
12 |
13 |
13 |
14 |
13 |
17 |
12 |
11 |
13 |
6 |
15 |
17 |
15 |
15 |
17 |
12 |
17 |
14 |
8 |
13 |
12 |
12 |
13 |
10 |
10 |
17 |
14 |
14 |
15 |
9 |
18 |
10 |
17 |
7 |
9 |
11 |
9 |
16 |
15 |
6 |
9 |
11 |
17 |
14 |
16 |
16 |
16 |
11 |
13 |
14 |
15 |
11 |
7 |
9. |
13 |
16 |
17 |
16 |
12 |
17 |
16 |
15 |
13 |
13 |
16 |
14 |
14 |
14 |
16 |
|
15 |
5 |
14 |
11 |
16 |
16 |
14 |
11 |
14 |
15 |
12 |
14 |
16 |
17 |
14 |
16 |
16 |
12 |
16 |
16 |
15 |
13 |
14 |
17 |
10 |
13 |
12 |
10 |
16 |
16 |
19 |
14 |
14 |
16 |
16 |
16 |
12 |
12 |
14 |
16 |
11 |
16 |
10 |
16 |
15 |
14 |
13 |
15 |
10 |
14 |
14 |
12 |
15 |
12 |
15 |
16 |
12 |
17 |
16 |
17 |
15 |
13 |
17 |
16 |
13 |
12 |
15 |
15 |
10 |
14 |
16 |
11 |
14 |
12 |
12 |
14 |
19 |
17 |
14 |
15 |
15 |
7 |
16 |
14 |
11 |
10. |
14 |
13 |
16 |
11 |
12 |
11 |
8 |
12 |
10 |
16 |
15 |
15 |
15 |
9 |
15 |
|
13 |
11 |
13 |
14 |
14 |
16 |
11 |
13 |
15 |
16 |
11 |
16 |
18 |
14 |
15 |
14 |
13 |
15 |
12 |
16 |
14 |
15 |
14 |
13 |
14 |
17 |
17 |
12 |
18 |
15 |
13 |
15 |
10 |
12 |
12 |
4 |
15 |
14 |
10 |
16 |
15 |
18 |
18 |
14 |
7 |
11 |
14 |
14 |
14 |
4 |
13 |
16 |
15 |
11 |
10 |
16 |
17 |
11 |
12 |
17 |
14 |
15 |
14 |
13 |
13 |
17 |
15 |
5 |
17 |
13 |
10 |
15 |
14 |
11 |
13 |
9 |
15 |
11 |
12 |
17 |
15 |
14 |
16 |
17 |
15 |
11. |
17 |
16 |
16 |
16 |
12 |
16 |
15 |
13 |
17 |
15 |
16 |
8 |
16 |
14 |
12 |
|
15 |
13 |
13 |
13 |
17 |
17 |
13 |
12 |
14 |
16 |
17 |
15 |
14 |
15 |
15 |
15 |
12 |
14 |
11 |
7 |
14 |
17 |
16 |
15 |
15 |
15 |
15 |
16 |
18 |
14 |
17 |
13 |
12 |
11 |
15 |
14 |
13 |
3 |
13 |
4 |
13 |
13 |
14 |
16 |
7 |
13 |
14 |
13 |
17 |
15 |
15 |
18 |
10 |
13 |
11 |
19 |
16 |
10 |
11 |
16 |
15 |
12 |
16 |
14 |
10 |
14 |
17 |
16 |
8 |
12 |
15 |
16 |
15 |
16 |
9 |
18 |
16 |
15 |
12 |
16 |
12 |
14 |
15 |
13 |
8 |
12. |
14 |
13 |
16 |
11 |
12 |
11 |
8 |
12 |
10 |
16 |
15 |
15 |
15 |
9 |
15 |
|
13 |
11 |
13 |
14 |
14 |
16 |
11 |
13 |
15 |
16 |
11 |
16 |
18 |
14 |
15 |
14 |
13 |
15 |
12 |
16 |
14 |
15 |
14 |
13 |
14 |
17 |
17 |
12 |
18 |
15 |
13 |
15 |
10 |
12 |
12 |
4 |
15 |
14 |
10 |
16 |
15 |
18 |
18 |
14 |
7 |
11 |
14 |
14 |
14 |
4 |
13 |
16 |
15 |
11 |
10 |
16 |
17 |
11 |
12 |
17 |
14 |
15 |
14 |
13 |
13 |
17 |
15 |
5 |
17 |
13 |
10 |
15 |
14 |
11 |
13 |
9 |
15 |
11 |
12 |
17 |
15 |
14 |
16 |
17 |
15 |
13. |
16 |
16 |
10 |
16 |
17 |
14 |
16 |
16 |
16 |
14 |
17 |
17 |
12 |
13 |
10 |
|
15 |
16 |
15 |
15 |
16 |
15 |
12 |
15 |
17 |
14 |
16 |
15 |
16 |
10 |
14 |
17 |
13 |
16 |
12 |
14 |
7 |
15 |
12 |
16 |
14 |
16 |
8 |
14 |
16 |
8 |
17 |
16 |
17 |
15 |
13 |
15 |
11 |
15 |
17 |
12 |
17 |
15 |
14 |
11 |
16 |
12 |
16 |
11 |
17 |
12 |
18 |
18 |
15 |
16 |
12 |
16 |
15 |
14 |
11 |
14 |
16 |
15 |
16 |
15 |
16 |
17 |
13 |
19 |
12 |
15 |
15 |
12 |
18 |
15 |
13 |
17 |
10 |
11 |
14 |
14 |
16 |
13 |
17 |
15 |
15 |
14. |
16 |
17 |
15 |
17 |
16 |
15 |
17 |
10 |
13 |
12 |
15 |
9 |
16 |
10 |
10 |
|
14 |
15 |
15 |
10 |
15 |
17 |
16 |
9 |
15 |
13 |
13 |
17 |
16 |
17 |
16 |
15 |
16 |
15 |
16 |
9 |
12 |
13 |
14 |
16 |
12 |
16 |
10 |
16 |
15 |
18 |
11 |
10 |
14 |
10 |
14 |
14 |
15 |
17 |
14 |
14 |
16 |
11 |
16 |
14 |
18 |
12 |
13 |
16 |
4 |
15 |
13 |
10 |
17 |
16 |
10 |
14 |
17 |
15 |
15 |
12 |
16 |
15 |
17 |
17 |
15 |
16 |
14 |
17 |
14 |
17 |
14 |
13 |
15 |
14 |
17 |
14 |
15 |
14 |
19 |
13 |
13 |
14 |
16 |
17 |
9 |
15. |
16 |
18 |
15 |
16 |
12 |
17 |
16 |
15 |
14 |
15 |
17 |
15 |
14 |
10 |
13 |
|
12 |
17 |
16 |
17 |
16 |
10 |
16 |
18 |
14 |
15 |
17 |
16 |
12 |
13 |
12 |
16 |
13 |
16 |
12 |
16 |
7 |
14 |
16 |
18 |
16 |
13 |
16 |
14 |
17 |
16 |
15 |
16 |
15 |
16 |
15 |
14 |
14 |
13 |
14 |
17 |
13 |
15 |
13 |
15 |
13 |
18 |
13 |
17 |
10 |
16 |
18 |
12 |
15 |
11 |
16 |
12 |
16 |
19 |
16 |
13 |
15 |
16 |
13 |
16 |
17 |
14 |
18 |
16 |
14 |
12 |
14 |
14 |
15 |
13 |
16 |
15 |
14 |
14 |
15 |
16 |
17 |
16 |
12 |
15 |
13 |
16. |
13 |
15 |
14 |
17 |
10 |
17 |
17 |
16 |
17 |
18 |
16 |
13 |
11 |
15 |
16 |
|
14 |
16 |
17 |
13 |
18 |
14 |
16 |
14 |
11 |
14 |
16 |
12 |
14 |
13 |
14 |
17 |
14 |
17 |
12 |
10 |
14 |
15 |
17 |
16 |
17 |
16 |
15 |
12 |
17 |
15 |
17 |
7 |
8 |
17 |
15 |
14 |
13 |
15 |
13 |
14 |
16 |
14 |
16 |
15 |
17 |
15 |
9 |
16 |
14 |
12 |
15 |
17 |
14 |
17 |
15 |
12 |
15 |
14 |
15 |
16 |
13 |
16 |
15 |
13 |
16 |
17 |
13 |
15 |
13 |
15 |
16 |
15 |
13 |
17 |
11 |
16 |
12 |
14 |
15 |
13 |
14 |
16 |
18 |
13 |
15 |
17. |
–7 |
–4 |
–9 |
–2 |
–6 |
–4 |
–8 |
–2 |
–5 |
4 |
–4 |
–6 |
–1 |
–5 |
1 |
|
–2 |
1 |
7 |
1 |
– 2 |
5 |
–1 |
–2 |
–4 |
–8 |
–1 |
–5 |
–2 |
–4 |
– 9 |
1 |
–4 |
7 |
–1 |
–5 |
–2 |
–4 |
–1 |
–5 |
– 2 |
–2 |
–6 |
1 |
–4 |
3 |
–6 |
–2 |
–7 |
–1 |
4 |
–9 |
–1 |
2 |
–6 |
1 |
–2 |
–5 |
–1 |
–4 |
– 6 |
1 |
–1 |
–8 |
3 |
–5 |
–4 |
3 |
–1 |
–8 |
1 |
–2 |
3 |
–5 |
–1 |
3 |
–7 |
1 |
–2 |
–4 |
1 |
– 6 |
– 1 |
3 |
– 4 |
1 |
– 1 |
– 4 |
– 5 |
3 |
– 2 |
1 |
– 2 |
4 |
1 |
– 5 |
3 |
– 2 |
– 4 |
– 1 |
–9 |
18. |
3 |
6 |
1 |
5 |
8 |
8 |
5 |
3 |
9 |
5 |
6 |
7 |
12 |
3 |
5 |
|
1 |
6 |
8 |
11 |
6 |
9 |
6 |
5 |
5 |
11 |
8 |
5 |
6 |
3 |
9 |
3 |
7 |
6 |
9 |
5 |
3 |
9 |
6 |
11 |
5 |
6 |
13 |
11 |
3 |
2 |
5 |
8 |
1 |
3 |
8 |
9 |
10 |
5 |
12 |
8 |
5 |
11 |
5 |
6 |
7 |
3 |
6 |
9 |
7 |
6 |
5 |
9 |
3 |
9 |
12 |
8 |
11 |
5 |
13 |
8 |
12 |
7 |
8 |
1 |
6 |
1 |
12 |
9 |
7 |
13 |
8 |
13 |
11 |
14 |
8 |
6 |
14 |
3 |
12 |
9 |
7 |
12 |
8 |
13 |
2 |
19. |
4 |
2 |
6 |
5 |
4 |
6 |
3 |
7 |
5 |
8 |
6 |
5 |
3 |
9 |
7 |
|
2 |
5 |
10 |
0 |
4 |
10 |
7 |
8 |
5 |
4 |
6 |
5 |
3 |
6 |
9 |
8 |
6 |
2 |
3 |
1 |
5 |
4 |
6 |
7 |
5 |
6 |
4 |
7 |
6 |
3 |
2 |
5 |
0 |
6 |
4 |
9 |
3 |
7 |
4 |
6 |
5 |
4 |
8 |
5 |
11 |
3 |
6 |
9 |
1 |
6 |
5 |
9 |
3 |
9 |
12 |
8 |
11 |
5 |
13 |
8 |
12 |
0 |
8 |
1 |
6 |
1 |
12 |
9 |
5 |
13 |
8 |
13 |
11 |
14 |
8 |
6 |
7 |
3 |
12 |
9 |
5 |
12 |
8 |
6 |
7 |
20. |
17 |
18 |
19 |
10 |
21 |
17 |
18 |
19 |
10 |
21 |
18 |
23 |
17 |
11 |
18 |
|
18 |
23 |
17 |
11 |
18 |
18 |
17 |
26 |
11 |
23 |
18 |
17 |
26 |
11 |
23 |
20 |
17 |
20 |
12 |
22 |
20 |
17 |
20 |
12 |
22 |
21 |
19 |
25 |
13 |
17 |
21 |
19 |
25 |
13 |
17 |
19 |
17 |
18 |
11 |
19 |
19 |
17 |
18 |
11 |
19 |
20 |
19 |
21 |
13 |
22 |
20 |
19 |
21 |
13 |
22 |
17 |
17 |
19 |
12 |
22 |
17 |
17 |
19 |
12 |
22 |
18 |
19 |
21 |
12 |
25 |
18 |
19 |
21 |
12 |
25 |
17 |
20 |
21 |
13 |
24 |
17 |
20 |
21 |
13 |
24 |
21. |
33 |
34 |
44 |
42 |
35 |
46 |
36 |
44 |
35 |
44 |
30 |
34 |
38 |
41 |
36 |
|
40 |
47 |
46 |
47 |
38 |
39 |
34 |
45 |
36 |
39 |
34 |
53 |
41 |
54 |
43 |
35 |
38 |
45 |
41 |
50 |
34 |
36 |
49 |
46 |
43 |
32 |
34 |
48 |
40 |
39 |
34 |
45 |
49 |
46 |
40 |
32 |
36 |
36 |
31 |
49 |
38 |
47 |
43 |
51 |
48 |
39 |
36 |
42 |
42 |
39 |
34 |
51 |
43 |
35 |
53 |
34 |
35 |
47 |
43 |
47 |
36 |
46 |
40 |
57 |
44 |
35 |
34 |
39 |
50 |
36 |
36 |
47 |
41 |
57 |
43 |
45 |
39 |
52 |
43 |
44 |
35 |
50 |
44 |
49 |
54 |
22. |
44 |
38 |
41 |
49 |
48 |
34 |
46 |
47 |
35 |
42 |
45 |
44 |
37 |
48 |
34 |
|
39 |
49 |
46 |
45 |
44 |
49 |
39 |
42 |
49 |
46 |
38 |
41 |
48 |
43 |
31 |
47 |
46 |
37 |
45 |
44 |
44 |
46 |
59 |
49 |
44 |
53 |
34 |
45 |
44 |
38 |
39 |
35 |
51 |
47 |
45 |
46 |
41 |
43 |
45 |
48 |
46 |
47 |
48 |
44 |
44 |
44 |
41 |
46 |
44 |
53 |
34 |
53 |
49 |
38 |
41 |
47 |
42 |
48 |
50 |
49 |
41 |
33 |
48 |
48 |
49 |
40 |
41 |
36 |
51 |
49 |
41 |
45 |
45 |
49 |
34 |
46 |
36 |
42 |
38 |
47 |
42 |
53 |
43 |
45 |
44 |
23. |
33 |
30 |
44 |
42 |
45 |
46 |
36 |
44 |
42 |
44 |
30 |
34 |
38 |
41 |
36 |
|
40 |
37 |
46 |
47 |
38 |
40 |
37 |
46 |
47 |
38 |
40 |
37 |
46 |
47 |
38 |
35 |
38 |
45 |
41 |
50 |
34 |
36 |
49 |
46 |
43 |
32 |
34 |
48 |
40 |
39 |
34 |
45 |
49 |
46 |
40 |
32 |
36 |
36 |
31 |
49 |
38 |
47 |
43 |
51 |
48 |
39 |
36 |
42 |
42 |
39 |
34 |
51 |
43 |
35 |
53 |
34 |
35 |
47 |
45 |
47 |
36 |
46 |
40 |
41 |
44 |
35 |
34 |
39 |
50 |
36 |
36 |
47 |
41 |
35 |
43 |
45 |
39 |
42 |
43 |
44 |
35 |
50 |
44 |
49 |
44 |
24. |
44 |
38 |
41 |
49 |
48 |
34 |
46 |
47 |
55 |
32 |
45 |
44 |
37 |
48 |
34 |
|
39 |
49 |
46 |
35 |
44 |
49 |
39 |
42 |
49 |
46 |
38 |
41 |
48 |
53 |
31 |
47 |
46 |
37 |
45 |
44 |
44 |
46 |
59 |
49 |
44 |
53 |
34 |
45 |
54 |
48 |
39 |
35 |
41 |
54 |
45 |
46 |
41 |
43 |
45 |
38 |
46 |
47 |
48 |
44 |
44 |
44 |
41 |
46 |
53 |
53 |
34 |
53 |
49 |
38 |
41 |
47 |
42 |
48 |
50 |
49 |
41 |
33 |
48 |
48 |
49 |
40 |
41 |
36 |
51 |
55 |
41 |
55 |
45 |
49 |
34 |
53 |
36 |
42 |
38 |
54 |
42 |
53 |
53 |
45 |
44 |
25. |
38 |
38 |
42 |
42 |
50 |
41 |
55 |
41 |
44 |
41 |
48 |
42 |
40 |
45 |
55 |
|
36 |
53 |
53 |
44 |
41 |
36 |
41 |
40 |
56 |
41 |
38 |
41 |
53 |
35 |
43 |
38 |
43 |
40 |
58 |
42 |
42 |
45 |
53 |
43 |
48 |
47 |
45 |
45 |
47 |
53 |
41 |
51 |
56 |
45 |
36 |
41 |
40 |
46 |
41 |
49 |
43 |
43 |
41 |
38 |
43 |
47 |
41 |
46 |
46 |
39 |
45 |
46 |
54 |
47 |
39 |
41 |
53 |
43 |
53 |
37 |
40 |
48 |
37 |
41 |
41 |
38 |
42 |
39 |
41 |
39 |
54 |
47 |
51 |
43 |
44 |
47 |
46 |
53 |
51 |
57 |
50 |
50 |
51 |
45 |
51 |
26. |
52 |
56 |
58 |
55 |
67 |
70 |
63 |
64 |
68 |
62 |
65 |
74 |
60 |
59 |
72 |
|
54 |
58 |
61 |
57 |
46 |
73 |
70 |
66 |
61 |
64 |
54 |
64 |
73 |
61 |
75 |
53 |
73 |
65 |
59 |
59 |
72 |
63 |
65 |
56 |
60 |
58 |
70 |
71 |
53 |
60 |
76 |
62 |
71 |
61 |
60 |
64 |
72 |
68 |
59 |
68 |
54 |
76 |
65 |
62 |
61 |
76 |
73 |
67 |
57 |
56 |
63 |
73 |
67 |
58 |
59 |
70 |
77 |
63 |
55 |
67 |
64 |
61 |
70 |
66 |
69 |
72 |
65 |
67 |
57 |
56 |
70 |
71 |
66 |
73 |
70 |
63 |
69 |
72 |
61 |
64 |
67 |
61 |
72 |
63 |
57 |
27. |
65 |
51 |
57 |
68 |
53 |
67 |
61 |
58 |
61 |
54 |
67 |
73 |
56 |
62 |
63 |
|
70 |
66 |
61 |
72 |
48 |
58 |
55 |
67 |
68 |
66 |
67 |
67 |
70 |
50 |
51 |
63 |
63 |
57 |
67 |
53 |
61 |
73 |
46 |
62 |
48 |
52 |
79 |
66 |
68 |
63 |
62 |
53 |
72 |
49 |
55 |
56 |
68 |
61 |
67 |
62 |
65 |
68 |
64 |
62 |
47 |
64 |
70 |
69 |
59 |
68 |
52 |
66 |
66 |
62 |
49 |
75 |
74 |
61 |
71 |
58 |
68 |
64 |
57 |
60 |
53 |
68 |
64 |
65 |
77 |
73 |
64 |
83 |
73 |
60 |
51 |
62 |
70 |
72 |
70 |
68 |
51 |
62 |
67 |
73 |
48 |
28. |
64 |
68 |
54 |
68 |
74 |
73 |
65 |
67 |
51 |
56 |
62 |
59 |
67 |
57 |
72 |
|
73 |
57 |
66 |
61 |
74 |
64 |
70 |
68 |
69 |
68 |
74 |
62 |
67 |
58 |
70 |
67 |
74 |
58 |
63 |
64 |
70 |
72 |
64 |
58 |
62 |
69 |
58 |
57 |
74 |
58 |
67 |
70 |
68 |
61 |
58 |
72 |
69 |
57 |
58 |
59 |
65 |
61 |
64 |
46 |
51 |
64 |
66 |
64 |
68 |
72 |
61 |
73 |
70 |
55 |
68 |
64 |
67 |
63 |
70 |
66 |
61 |
60 |
74 |
61 |
63 |
66 |
69 |
63 |
66 |
52 |
67 |
63 |
69 |
56 |
57 |
68 |
69 |
70 |
70 |
54 |
67 |
64 |
60 |
58 |
69 |
29. |
46 |
39 |
44 |
41 |
49 |
39 |
40 |
43 |
44 |
43 |
40 |
43 |
37 |
37 |
48 |
|
42 |
37 |
46 |
38 |
41 |
43 |
43 |
41 |
42 |
49 |
46 |
48 |
36 |
45 |
43 |
42 |
37 |
37 |
37 |
55 |
44 |
45 |
41 |
45 |
41 |
41 |
38 |
38 |
45 |
54 |
40 |
44 |
37 |
48 |
40 |
38 |
41 |
36 |
43 |
45 |
41 |
45 |
43 |
36 |
31 |
42 |
37 |
42 |
46 |
53 |
45 |
35 |
46 |
42 |
42 |
46 |
37 |
36 |
48 |
50 |
39 |
41 |
38 |
47 |
43 |
41 |
44 |
39 |
36 |
51 |
38 |
38 |
43 |
39 |
50 |
40 |
38 |
45 |
41 |
38 |
45 |
40 |
37 |
52 |
43 |
30. |
37 |
40 |
41 |
39 |
36 |
40 |
42 |
39 |
40 |
36 |
44 |
36 |
44 |
41 |
38 |
|
33 |
44 |
34 |
42 |
39 |
42 |
44 |
38 |
40 |
41 |
42 |
38 |
44 |
36 |
35 |
39 |
42 |
40 |
39 |
36 |
44 |
40 |
36 |
40 |
40 |
40 |
36 |
42 |
44 |
35 |
36 |
44 |
33 |
34 |
39 |
34 |
42 |
38 |
39 |
43 |
44 |
39 |
38 |
42 |
41 |
40 |
35 |
38 |
39 |
42 |
42 |
39 |
38 |
36 |
41 |
41 |
40 |
33 |
50 |
36 |
40 |
41 |
40 |
35 |
43 |
40 |
42 |
40 |
41 |
34 |
41 |
40 |
38 |
42 |
40 |
38 |
41 |
43 |
39 |
42 |
37 |
37 |
40 |
41 |
38 |
31. |
17 |
14 |
16 |
14 |
18 |
20 |
18 |
18 |
10 |
20 |
17 |
19 |
21 |
16 |
20 |
|
18 |
19 |
25 |
15 |
17 |
17 |
17 |
22 |
17 |
19 |
17 |
21 |
13 |
29 |
21 |
14 |
17 |
15 |
18 |
23 |
18 |
18 |
18 |
10 |
27 |
19 |
14 |
16 |
17 |
24 |
17 |
17 |
18 |
11 |
23 |
17 |
18 |
12 |
16 |
31 |
19 |
18 |
17 |
11 |
18 |
17 |
18 |
19 |
15 |
18 |
27 |
17 |
19 |
12 |
25 |
24 |
18 |
16 |
14 |
19 |
18 |
27 |
21 |
20 |
30 |
23 |
27 |
14 |
13 |
18 |
18 |
17 |
20 |
24 |
16 |
20 |
18 |
18 |
10 |
30 |
19 |
19 |
20 |
30 |
22 |
32. |
19 |
18 |
21 |
23 |
17 |
17 |
18 |
19 |
10 |
21 |
19 |
19 |
22 |
29 |
18 |
|
18 |
23 |
17 |
11 |
18 |
19 |
19 |
21 |
34 |
21 |
18 |
17 |
26 |
11 |
23 |
18 |
18 |
19 |
21 |
18 |
20 |
17 |
20 |
12 |
22 |
25 |
20 |
17 |
46 |
19 |
21 |
19 |
25 |
13 |
17 |
26 |
20 |
21 |
16 |
20 |
19 |
17 |
18 |
11 |
19 |
24 |
20 |
21 |
46 |
18 |
20 |
19 |
21 |
13 |
22 |
20 |
19 |
18 |
16 |
18 |
17 |
17 |
19 |
12 |
22 |
17 |
19 |
18 |
30 |
20 |
18 |
19 |
21 |
12 |
25 |
19 |
18 |
20 |
34 |
17 |
17 |
20 |
21 |
13 |
24 |
33. |
42 |
37 |
39 |
39 |
42 |
41 |
44 |
38 |
38 |
46 |
45 |
39 |
44 |
44 |
45 |
|
39 |
44 |
44 |
42 |
47 |
43 |
35 |
43 |
43 |
46 |
41 |
44 |
39 |
41 |
38 |
42 |
37 |
40 |
42 |
48 |
41 |
38 |
46 |
43 |
40 |
37 |
37 |
46 |
42 |
47 |
42 |
44 |
34 |
45 |
44 |
37 |
49 |
45 |
40 |
50 |
40 |
36 |
41 |
40 |
44 |
39 |
38 |
42 |
41 |
46 |
44 |
36 |
41 |
41 |
42 |
38 |
45 |
40 |
40 |
49 |
35 |
35 |
42 |
43 |
41 |
48 |
45 |
40 |
45 |
41 |
36 |
34 |
41 |
47 |
40 |
38 |
44 |
45 |
46 |
42 |
43 |
39 |
36 |
44 |
42 |
34. |
14 |
5 |
4 |
5 |
9 |
3 |
4 |
4 |
4 |
3 |
7 |
3 |
5 |
4 |
4 |
|
4 |
11 |
4 |
4 |
4 |
18 |
5 |
4 |
5 |
14 |
5 |
5 |
4 |
9 |
12 |
17 |
5 |
4 |
4 |
5 |
4 |
12 |
11 |
4 |
4 |
14 |
4 |
15 |
4 |
17 |
14 |
20 |
19 |
21 |
19 |
14 |
4 |
4 |
4 |
11 |
10 |
23 |
22 |
14 |
18 |
11 |
4 |
4 |
4 |
10 |
12 |
11 |
10 |
9 |
7 |
13 |
24 |
4 |
16 |
12 |
14 |
15 |
14 |
8 |
6 |
11 |
5 |
5 |
5 |
11 |
16 |
12 |
11 |
10 |
11 |
9 |
3 |
4 |
5 |
10 |
13 |
18 |
12 |
13 |
12 |
35. |
3 |
3 |
3 |
4 |
1 |
9 |
2 |
7 |
4 |
6 |
5 |
11 |
4 |
7 |
6 |
|
6 |
2 |
6 |
5 |
3 |
6 |
4 |
5 |
5 |
4 |
6 |
6 |
4 |
6 |
7 |
4 |
4 |
5 |
2 |
3 |
5 |
4 |
6 |
4 |
5 |
5 |
1 |
8 |
3 |
2 |
3 |
7 |
4 |
4 |
4 |
3 |
7 |
7 |
4 |
5 |
1 |
5 |
2 |
2 |
7 |
8 |
4 |
5 |
3 |
5 |
4 |
6 |
2 |
6 |
4 |
3 |
0 |
9 |
6 |
6 |
2 |
9 |
5 |
5 |
7 |
10 |
4 |
2 |
3 |
5 |
7 |
5 |
4 |
8 |
7 |
6 |
4 |
1 |
4 |
4 |
2 |
3 |
8 |
9 |
4 |
36. |
4 |
3 |
2 |
3 |
4 |
4 |
6 |
7 |
2 |
7 |
2 |
3 |
5 |
4 |
5 |
|
5 |
8 |
3 |
7 |
9 |
3 |
3 |
5 |
4 |
1 |
4 |
9 |
2 |
4 |
6 |
3 |
10 |
6 |
6 |
6 |
3 |
6 |
3 |
4 |
5 |
7 |
4 |
5 |
2 |
2 |
5 |
3 |
5 |
5 |
5 |
6 |
5 |
4 |
4 |
10 |
5 |
7 |
2 |
2 |
5 |
4 |
4 |
4 |
4 |
3 |
2 |
6 |
3 |
4 |
5 |
3 |
4 |
1 |
6 |
6 |
6 |
3 |
7 |
3 |
5 |
0 |
4 |
11 |
3 |
4 |
6 |
1 |
4 |
4 |
4 |
5 |
4 |
4 |
3 |
6 |
3 |
7 |
7 |
4 |
7 |
37. |
5 |
6 |
3 |
8 |
3 |
2 |
5 |
5 |
2 |
7 |
7 |
5 |
4 |
7 |
3 |
|
10 |
2 |
2 |
6 |
4 |
3 |
5 |
3 |
5 |
4 |
8 |
2 |
5 |
5 |
3 |
3 |
1 |
4 |
5 |
4 |
3 |
5 |
10 |
7 |
4 |
4 |
7 |
5 |
8 |
6 |
7 |
4 |
4 |
6 |
2 |
3 |
7 |
5 |
5 |
3 |
8 |
3 |
4 |
5 |
4 |
2 |
6 |
4 |
9 |
4 |
5 |
10 |
3 |
4 |
6 |
5 |
3 |
2 |
7 |
0 |
7 |
3 |
10 |
5 |
7 |
1 |
1 |
7 |
4 |
3 |
1 |
4 |
3 |
4 |
6 |
8 |
8 |
4 |
6 |
5 |
7 |
1 |
5 |
7 |
2 |
38. |
41 |
34 |
36 |
37 |
36 |
34 |
43 |
33 |
31 |
40 |
39 |
37 |
37 |
38 |
35 |
|
31 |
37 |
41 |
42 |
39 |
41 |
35 |
33 |
36 |
38 |
32 |
36 |
44 |
34 |
38 |
48 |
38 |
33 |
38 |
39 |
41 |
40 |
42 |
36 |
33 |
42 |
35 |
42 |
34 |
39 |
43 |
40 |
41 |
33 |
45 |
44 |
29 |
39 |
40 |
37 |
35 |
34 |
39 |
41 |
32 |
42 |
41 |
35 |
37 |
35 |
33 |
34 |
42 |
40 |
44 |
35 |
38 |
32 |
38 |
34 |
31 |
39 |
35 |
42 |
37 |
40 |
33 |
30 |
38 |
34 |
30 |
30 |
32 |
36 |
38 |
40 |
33 |
37 |
37 |
42 |
36 |
32 |
41 |
33 |
40 |
39. |
2 |
3 |
2 |
1 |
5 |
3 |
7 |
4 |
3 |
2 |
5 |
4 |
2 |
2 |
6 |
|
4 |
– 1 |
0 |
4 |
– 2 |
4 |
5 |
3 |
3 |
8 |
6 |
4 |
6 |
7 |
6 |
2 |
4 |
3 |
– 1 |
4 |
3 |
2 |
4 |
5 |
1 |
1 |
2 |
1 |
1 |
8 |
7 |
1 |
6 |
0 |
4 |
0 |
3 |
2 |
3 |
9 |
6 |
4 |
9 |
5 |
4 |
1 |
3 |
1 |
3 |
10 |
8 |
3 |
4 |
0 |
8 |
3 |
2 |
0 |
3 |
11 |
10 |
0 |
1 |
4 |
– 3 |
– 1 |
0 |
2 |
4 |
9 |
8 |
4 |
0 |
3 |
4 |
– 1 |
4 |
4 |
4 |
10 |
8 |
– 2 |
4 |
6 |
2 |
40. |
3 |
6 |
6 |
– 3 |
– 1 |
2 |
6 |
8 |
4 |
11 |
1 |
8 |
7 |
– 1 |
3 |
|
0 |
2 |
6 |
4 |
0 |
3 |
6 |
5 |
2 |
3 |
2 |
2 |
6 |
4 |
5 |
4 |
– 2 |
– 2 |
1 |
0 |
1 |
3 |
7 |
7 |
6 |
– 3 |
– 1 |
2 |
– 2 |
5 |
3 |
4 |
9 |
10 |
8 |
1 |
1 |
1 |
1 |
8 |
6 |
8 |
3 |
11 |
0 |
– 1 |
– 1 |
– 1 |
5 |
3 |
9 |
0 |
12 |
11 |
3 |
– 2 |
– 1 |
– 2 |
5 |
4 |
10 |
7 |
2 |
0 |
7 |
4 |
– 1 |
– 2 |
7 |
4 |
10 |
– 2 |
5 |
2 |
0 |
– 3 |
– 1 |
2 |
9 |
3 |
7 |
1 |
2 |
1 |
4 |
41. |
10 |
13 |
11 |
6 |
18 |
13 |
12 |
22 |
14 |
18 |
7 |
13 |
12 |
11 |
14 |
|
16 |
10 |
14 |
14 |
17 |
9 |
13 |
18 |
15 |
21 |
17 |
10 |
16 |
15 |
16 |
14 |
22 |
18 |
16 |
21 |
20 |
11 |
20 |
17 |
18 |
10 |
20 |
16 |
17 |
22 |
17 |
14 |
15 |
13 |
17 |
13 |
18 |
16 |
11 |
18 |
17 |
12 |
24 |
18 |
9 |
11 |
13 |
13 |
14 |
16 |
15 |
15 |
22 |
19 |
17 |
13 |
15 |
14 |
14 |
15 |
18 |
16 |
26 |
18 |
19 |
9 |
13 |
13 |
14 |
19 |
18 |
15 |
22 |
16 |
17 |
10 |
12 |
10 |
13 |
15 |
15 |
15 |
21 |
14 |
18 |
42. |
14 |
21 |
19 |
19 |
25 |
20 |
15 |
23 |
23 |
19 |
16 |
26 |
19 |
13 |
24 |
|
23 |
19 |
23 |
19 |
17 |
16 |
20 |
16 |
18 |
26 |
24 |
19 |
26 |
23 |
14 |
16 |
23 |
21 |
21 |
26 |
24 |
18 |
24 |
19 |
18 |
15 |
25 |
21 |
22 |
27 |
26 |
19 |
24 |
19 |
21 |
17 |
24 |
20 |
22 |
25 |
26 |
18 |
20 |
16 |
19 |
19 |
26 |
19 |
22 |
23 |
26 |
15 |
20 |
15 |
11 |
14 |
25 |
20 |
22 |
25 |
19 |
12 |
19 |
16 |
20 |
13 |
20 |
19 |
17 |
20 |
20 |
11 |
18 |
10 |
22 |
17 |
26 |
23 |
17 |
26 |
23 |
19 |
11 |
17 |
19 |
43. |
8 |
11 |
9 |
4 |
12 |
8 |
8 |
15 |
12 |
14 |
8 |
13 |
11 |
8 |
15 |
|
9 |
10 |
13 |
12 |
13 |
10 |
17 |
14 |
8 |
12 |
11 |
11 |
15 |
12 |
11 |
14 |
18 |
15 |
7 |
12 |
8 |
11 |
17 |
10 |
12 |
12 |
15 |
13 |
6 |
12 |
8 |
10 |
16 |
12 |
10 |
11 |
20 |
14 |
9 |
14 |
10 |
10 |
17 |
13 |
11 |
13 |
17 |
11 |
8 |
18 |
11 |
11 |
18 |
13 |
12 |
9 |
14 |
10 |
10 |
15 |
12 |
13 |
15 |
14 |
11 |
6 |
12 |
8 |
10 |
16 |
14 |
9 |
17 |
13 |
15 |
5 |
8 |
5 |
9 |
12 |
10 |
9 |
20 |
14 |
12 |
44. |
16 |
24 |
18 |
17 |
24 |
18 |
14 |
15 |
13 |
19 |
16 |
26 |
18 |
14 |
26 |
|
20 |
11 |
21 |
18 |
16 |
15 |
24 |
20 |
21 |
28 |
20 |
12 |
19 |
18 |
20 |
16 |
20 |
17 |
17 |
24 |
19 |
12 |
21 |
19 |
18 |
15 |
26 |
21 |
17 |
25 |
18 |
15 |
18 |
18 |
19 |
15 |
26 |
20 |
16 |
23 |
18 |
15 |
20 |
16 |
20 |
18 |
24 |
18 |
17 |
27 |
19 |
15 |
20 |
19 |
17 |
15 |
22 |
17 |
12 |
25 |
21 |
16 |
23 |
20 |
19 |
15 |
20 |
17 |
16 |
21 |
20 |
17 |
25 |
20 |
18 |
16 |
25 |
19 |
15 |
19 |
19 |
17 |
25 |
21 |
19 |
45. |
20 |
22 |
21 |
17 |
12 |
10 |
18 |
23 |
23 |
22 |
11 |
18 |
13 |
19 |
11 |
|
11 |
16 |
22 |
16 |
21 |
10 |
15 |
15 |
17 |
15 |
12 |
14 |
22 |
17 |
26 |
11 |
16 |
19 |
15 |
14 |
14 |
14 |
17 |
17 |
20 |
12 |
19 |
24 |
19 |
17 |
16 |
13 |
17 |
16 |
18 |
12 |
21 |
17 |
15 |
15 |
14 |
16 |
19 |
22 |
23 |
17 |
14 |
12 |
10 |
15 |
15 |
20 |
21 |
26 |
25 |
18 |
10 |
12 |
11 |
17 |
16 |
18 |
26 |
22 |
22 |
18 |
10 |
9 |
13 |
22 |
20 |
18 |
24 |
27 |
25 |
17 |
12 |
15 |
17 |
23 |
23 |
19 |
26 |
18 |
20 |
46. |
3,9 |
3,7 |
3,2 |
3,9 |
4,0 |
3,6 |
3,8 |
3,6 |
4,0 |
3,9 |
3,8 |
3,6 |
4,1 |
3,7 |
3,6 |
|
3,9 |
4,2 |
3,7 |
3,5 |
4,1 |
3,4 |
3,1 |
4,6 |
4,0 |
4,1 |
4,0 |
4,1 |
4,2 |
3,8 |
4,0 |
3,5 |
3,8 |
3,9 |
3,8 |
3,6 |
4,2 |
3,9 |
4,1 |
3,7 |
3,6 |
3,4 |
4,5 |
3,7 |
4,0 |
4,1 |
3,8 |
3,5 |
4,0 |
4,2 |
3,9 |
3,9 |
4,4 |
3,6 |
3,7 |
3,9 |
4,3 |
4,0 |
3,9 |
4,1 |
3,5 |
4,2 |
4,4 |
4,4 |
3,6 |
3,8 |
4,0 |
3,6 |
4,3 |
3,7 |
3,8 |
4,2 |
4,0 |
4,6 |
3,9 |
3,5 |
3,8 |
3,5 |
3,9 |
4,3 |
3,6 |
4,1 |
3,9 |
3,9 |
3,8 |
4,1 |
3,6 |
4,1 |
3,6 |
4,1 |
3,7 |
4,2 |
4,1 |
4,4 |
4,1 |
3,8 |
3,9 |
3,6 |
3,7 |
3,9 |
4,0 |
47. |
3,7 |
4,5 |
3,7 |
4,4 |
4,0 |
4,3 |
4,6 |
4,4 |
4,2 |
4,7 |
4,1 |
4,0 |
3,8 |
4,8 |
4,2 |
|
4,7 |
4,2 |
3,8 |
4,0 |
4,4 |
4,7 |
3,5 |
3,3 |
4,3 |
4,6 |
4,1 |
4,4 |
4,2 |
3,8 |
4,3 |
4,6 |
3,8 |
4,2 |
3,8 |
4,7 |
4,0 |
4,3 |
4,6 |
4,2 |
4,0 |
4,9 |
3,4 |
4,0 |
4,3 |
3,8 |
4,2 |
3,8 |
4,7 |
4,2 |
4,4 |
4,0 |
4,4 |
4,2 |
4,4 |
4,0 |
4,4 |
4,1 |
4,4 |
4,6 |
3,8 |
3,1 |
4,0 |
4,6 |
4,1 |
3,8 |
4,1 |
4,0 |
4,2 |
3,8 |
4,3 |
3,6 |
4,6 |
4,1 |
4,0 |
4,2 |
4,6 |
4,2 |
4,3 |
4,8 |
4,2 |
4,1 |
4,6 |
4,7 |
4,2 |
4,6 |
4,3 |
4,4 |
4,2 |
3,8 |
4,7 |
3,7 |
3,7 |
4,3 |
3,8 |
4,2 |
4,7 |
4,3 |
3,3 |
4,3 |
3,8 |
48. |
20 |
19 |
19 |
13 |
20 |
13 |
21 |
20 |
19 |
22 |
18 |
19 |
19 |
11 |
22 |
|
23 |
18 |
16 |
17 |
22 |
17 |
19 |
19 |
15 |
12 |
22 |
16 |
20 |
17 |
21 |
18 |
18 |
18 |
16 |
15 |
20 |
19 |
21 |
20 |
23 |
17 |
25 |
25 |
21 |
24 |
22 |
23 |
20 |
22 |
21 |
19 |
26 |
26 |
23 |
20 |
20 |
21 |
23 |
25 |
22 |
17 |
24 |
24 |
12 |
16 |
15 |
20 |
20 |
24 |
20 |
18 |
20 |
20 |
14 |
25 |
17 |
21 |
24 |
20 |
19 |
18 |
17 |
17 |
22 |
17 |
20 |
18 |
20 |
18 |
20 |
19 |
19 |
19 |
15 |
16 |
22 |
21 |
23 |
22 |
21 |
49. |
17 |
17 |
20 |
19 |
17 |
22 |
18 |
22 |
19 |
18 |
17 |
12 |
19 |
17 |
20 |
|
23 |
20 |
21 |
20 |
21 |
18 |
17 |
13 |
17 |
17 |
26 |
19 |
18 |
19 |
20 |
17 |
18 |
21 |
14 |
18 |
23 |
23 |
17 |
17 |
19 |
17 |
18 |
19 |
18 |
19 |
22 |
24 |
19 |
18 |
17 |
17 |
14 |
21 |
18 |
18 |
19 |
22 |
18 |
18 |
18 |
17 |
16 |
15 |
18 |
17 |
25 |
18 |
18 |
19 |
17 |
16 |
20 |
17 |
17 |
21 |
20 |
19 |
18 |
18 |
17 |
19 |
17 |
17 |
18 |
21 |
21 |
20 |
18 |
18 |
19 |
18 |
17 |
17 |
17 |
23 |
22 |
21 |
18 |
17 |
17 |
50. |
18 |
17 |
15 |
16 |
18 |
17 |
11 |
13 |
27 |
17 |
16 |
17 |
15 |
20 |
18 |
|
17 |
26 |
14 |
25 |
18 |
17 |
17 |
17 |
17 |
18 |
17 |
24 |
23 |
25 |
23 |
15 |
16 |
17 |
17 |
16 |
20 |
23 |
26 |
23 |
14 |
17 |
16 |
17 |
17 |
19 |
19 |
14 |
24 |
24 |
24 |
16 |
19 |
16 |
20 |
18 |
16 |
25 |
23 |
25 |
23 |
16 |
15 |
17 |
17 |
17 |
18 |
23 |
26 |
23 |
23 |
19 |
16 |
15 |
21 |
20 |
17 |
14 |
23 |
25 |
14 |
18 |
15 |
17 |
19 |
22 |
16 |
25 |
24 |
23 |
25 |
18 |
16 |
17 |
18 |
17 |
22 |
24 |
25 |
13 |
24 |
1.2. Статистические оценки. Пусть требуется определить значение какого-либо параметра случайной величины . Во многих случаях хорошее приближение неизвестного параметра можно найти, используя выборку x1, x2, ..., xn значений . Полученное приближение n называют точечной оценкой параметра . При изучении свойств точечных оценок предполагают, что наблюдаемые в эксперименте значения xj случайной величины являются независимыми случайными величинами, распределенными так же, как и . Тогда n n(x1, x2, ..., xn) также является случайной величиной. Если выполняется равенство Mn , то оценка n называется несмещенной.
Для M и D в качестве точечных оценок естественно принять математическое ожидание и дисперсию эмпирического распределения (табл. на стр. 65):
– выборочное
(эмпирическое) математическое
ожидание;
– выборочная
(эмпирическая) дисперсия.
Оценка
является несмещенной, оценка
не является несмещенной. Несмещенной
оценкой для D
является исправленная выборочная
дисперсия, определяемая равенством
.
Квадратные корни
из
и
,
т. е.
и s, называют
соответственно выборочным квадратичным
отклонением и исправленным выборочным
квадратичным отклонением.
Вопрос о точности
приближения решается при помощи
интервальной оценки. Пусть 0 < < 1.
Если выполняется неравенство
l
, то
интервал
называют доверительным интервалом
для параметра
с надежностью .
Надежность в
соответствии с практической задачей
задают в пределах от 0,95 до 0,999. Тогда с
вероятностью, не меньшей ,
имеем
.
Если случайная
величина
распределена по нормальному закону и
известна дисперсия D
2,
то доверительный интервал для ее
математического ожидания имеет вид
,
где
.
Доверительный интервал для неизвестной дисперсии нормального распределения находят, используя распределение 2 с числом степеней свободы n – 1 1. Он имеет вид
где
,
.
(Таблица корней уравнения
имеется в конце данного пособия; табл.
3.)
Доверительный
интервал для неизвестного математического
ожидания нормально распределенной
случайной величины в случае, когда
дисперсия также неизвестна, можно найти,
используя таблицу корней уравнения
,
где случайная величина
распределена по закону Стьюдента с n
– 1 степенями свободы 2
(табл. 4). Этот интервал имеет вид
,
где
.
51. Контрольные измерения прочности бетона при сжатии дали следующие результаты (в Н/мм2): 43,4; 48,0; 46,1; 36,2; 45,3; 41,2. Найти: 1) выборочное математическое ожидание, выборочную и исправленную выборочную дисперсии случайной величины – прочности бетона при сжатии; 2) доверительный интервал для математического ожидания с надежностью 0,96, считая, что распределение является нормальным, а дисперсия известна и равна полученной выборочной дисперсии; 3) доверительный интервал для дисперсии с надежностью 0,96, считая распределение нормальным; 4) доверительный интервал для математического ожидания с надежностью 0,9, считая, что распределение является нормальным, а дисперсия неизвестна.
Решение.
1)
;
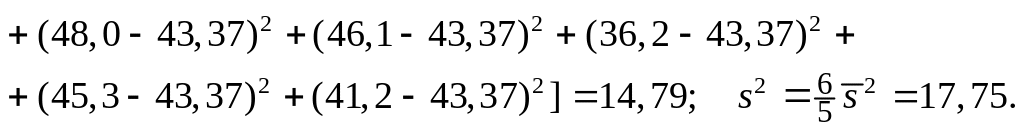
2)
По условию 2
14,79, откуда
.
(z) /2 0,96 / 2 0,48, откуда по таблице находим z 2,05;
;
;
доверительный интервал (40,15; 46,59); M 43,37 3,22.
3)
По таблице 3 на пересечении строки,
соответствующей числу степеней
свободы n
– 1
5 и столбцов, соответствующих значениям
q,
равным
и
,
находим решения уравнений
и
.
Получаем y
0,75 и z
13,4. Находим концы доверительного
интервала:
.
Искомый доверительный интервал для
D:
(6,62; 118,33).
4) По таблице 4 на пересечении строки, соответствующей числу степеней свободы n – 1 5 и столбца, соответствующего значению 0,9 находим решения уравнения P(| | < t) 0,9; получаем t 2,025. Находим концы доверительного интервала:
;
;
доверительный интервал (39,90; 46,84); M 43,37 3,47.
В задачах 52 – 95 для заданной выборки значений случайной величины требуется найти: 1) выборочное математическое ожидание, выборочную и исправленную выборочную дисперсии; 2) доверительный интервал для M с надежностью 0,99 при следующих предположениях: а) распределена по нормальному закону с дисперсией, равной целому числу, ближайшему к выборочной дисперсии; б) распределена по нормальному закону и ее дисперсия неизвестна; 3) для выборки объема n 32 (первые 2 строки таблицы) исправленную выборочную дисперсию и доверительный интервал для Dс надежностью 0,95, предполагая распределение нормальным.
52. Таблица из задачи 7. 53. Таблица из задачи 8.
54. Таблица из задачи 9. 55. Таблица из задачи 10.
56. Таблица из задачи 11. 57. Таблица из задачи 12.
58. Таблица из задачи 13. 59. Таблица из задачи 14.
60. Таблица из задачи 15. 61. Таблица из задачи 16.
62. Таблица из задачи 17. 63. Таблица из задачи 18.
64. Таблица из задачи 19. 65. Таблица из задачи 20.
66. Таблица из задачи 21. 67. Таблица из задачи 22.
68. Таблица из задачи 23. 69. Таблица из задачи 24.
70. Таблица из задачи 25. 71. Таблица из задачи 26.
72. Таблица из задачи 27. 73. Таблица из задачи 28.
74. Таблица из задачи 29. 75. Таблица из задачи 30.
76. Таблица из задачи 31. 77. Таблица из задачи 32.
78. Таблица из задачи 33. 79. Таблица из задачи 34.
80. Таблица из задачи 35. 81. Таблица из задачи 36.
82. Таблица из задачи 37. 83. Таблица из задачи 38.
84. Таблица из задачи 39. 85. Таблица из задачи 40.
86. Таблица из задачи 41. 87. Таблица из задачи 42.
88. Таблица из задачи 43. 89. Таблица из задачи 44.
90. Таблица из задачи 45. 91. Таблица из задачи 46.
92. Таблица из задачи 47. 93. Таблица из задачи 48.
94. Таблица из задачи 49. 95. Таблица из задачи 50.
1.3. Проверка статистических гипотез. Статистической гипотезой называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.
При проверке гипотезы могут быть допущена ошибка, состоящая в том, что будет отвергнута правильная гипотеза. Ее вероятность называют уровнем значимости и обозначают через .
Для проверки гипотезы рассматривают случайную величину K, которая выражается через эмпирические характеристики тех случайных величин, о которых говорится в гипотезе. Случайную величину K называют критерием для данной гипотезы.
Если в результате наблюдений получены выборки значений случайных величин, относительно которых сделана гипотеза, то эмпирические характеристики принимают определенное значение, а значит, и критерий K также принимает определенное значение. Это значение будем называть наблюдаемым и обозначать Kнабл.
Критической областью называют совокупность значений критерия, при которых основную гипотезу отвергают. Областью принятия гипотезы называют совокупность значений критерия, при которых основную гипотезу принимают.
Точки, отделяющие критическую область от области принятия гипотезы, называют критическими.
Критическую область вида (Kкр, ) называют правосторонней. Она имеет единственную критическую точку Kкр, определяемую равенством P(K > Kкр) .
Критическую область вида (–, Kкр) называют левосторонней. Она имеет единственную критическую точку Kкр, определяемую равенством P(K < Kкр) .
Односторонние критические области возникают, например, когда основная гипотеза имеет вид a b, а в качестве альтернативной выбрано одно из неравенств a < b, a > b. Если же альтернативная гипотеза имеет вид a b, то критическая область состоит из двух частей, соответствующих неравенствам a < b и a > b.
Критическую
область, являющуюся объединением
интервалов (–,
)
(
),
где
< 
называют двусторонней, она имеет
две критические точки: левую
и правую
которые при заданном уровне значимости
должны удовлетворять условию P(K
<
)
+ + P(K
>
)
.
Обычно критические точки находят из
уравнений P(K
<
)
P(K
>
)
/ 2. Это особенно удобно, если плотность
вероятностей f
случайной величины K
является четной функцией. В этом случае,
поскольку P(K
< –a)
P(K
> a), получаем
–
так что достаточно разыскать решение
только одного уравнения P(K
>
)
/ 2.
В качестве критерия
проверки гипотезы H0:
используют случайную величину
.
Случай 1:
и
заметно различаются и при этом
>
.
В этом случае используется альтернативная
гипотеза HА:
.
Вычисляют
,
Вычисляют
,
затем по таблице критических точек
распределения Фишера по уровню значимости
и числам степеней
свободы m – 1 и n
– 1 отыскивается критическая точка
Fкр(,
m – 1, n – 1).
Если Fнабл < Fкр, то основную гипотезу принимают; если же Fнабл > Fкр, то основную гипотезу отвергают.
Если
<
,
то можно аналогично использовать
левостороннюю критическую область, но
обычно, поскольку таблица не содержит
соответствующих критических точек,
снова используют правостороннюю
критическую область, взяв в качестве
критерия обратное отношение
.
Случай 2:
и
различаются мало, тогда в качестве
альтернативной берется гипотеза HА:
.
По уровню значимости /2
и числам степеней свободы m
– 1 и n – 1 (m – 1
– число степеней свободы распределения
с бóльшей выборочной дисперсией) ищут
( / 2, m – 1, n – 1),
а затем
.
Если
< Fнабл
<
,
основную гипотезу принимают, а при
Fнабл
<
или Fнабл
>
ее отвергают.
В качестве критерия проверки гипотезы H0: M M, т. е. a b выберем случайную величину
.
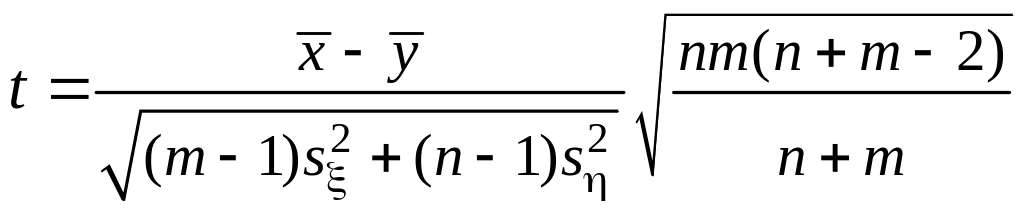Случай 1:
альтернативная гипотеза a
b.
Вычисляют
.
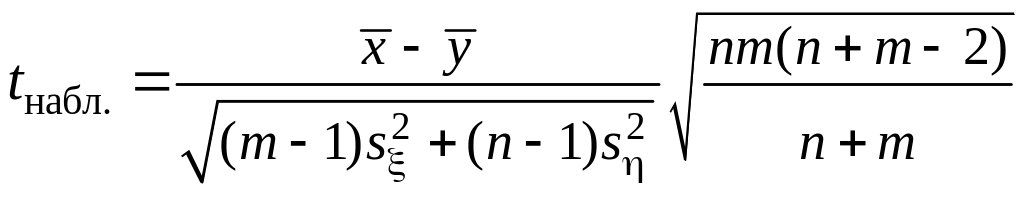Строится двусторонняя критическая область. Поэтому находят правую критическую точку по таблице критических точек распределения Стьюдента по уровню значимости / 2 и числу степеней свободы k m + n – 2.
Если
,
то основную гипотезу принимают.
Если
,
то основную гипотезу отвергают.
Случай 2:
альтернативная гипотеза a
> b. Строится
правосторонняя критическая область.
Единственную критическую точку находят
по уровню значимости
и числу степеней свободы n + m – 2
в таблице критических точек распределения
Стьюдента:
.
Если
,
то основная гипотеза принимается.
Если
,
то основную гипотезу отвергают.
Случай 3:
альтернативная гипотеза a
< b. В этом случае
строится левосторонняя критическая
область. Критическая точка
.
Если , то основная гипотеза принимается.
Если , то основную гипотезу отвергают.
В качестве критерия проверки гипотезы H0: M a выберем случайную величину
.
Этот критерий используется, когда объем выборки мал.
Случай 1:
альтернативная гипотеза
.
В этом случае строится двусторонняя
критическая область такая, чтобы
вероятность попадания значения t
в эту область в случае справедливости
основной гипотезы была равна принятому
уровню значимости .
Сначала вычисляют
,
потом находят критические точки.
Поскольку плотность вероятностей
распределения Стьюдента – четная
функция, критические точки симметричны
относительно нуля. Поэтому достаточно
найти правую критическую точку. Ее
находят по таблице критических точек
распределения Стьюдента по уровню
значимости / 2
и k
n – 1
(
).
Если , то основную гипотезу принимают.
Если , то основную гипотезу отвергают.
Случай 2:
альтернативная гипотеза
> a. Строится
правосторонняя критическая область.
Единственную критическую точку находят
по уровню значимости
и числу степеней свободы n – 1
в таблице критических точек распределения
Стьюдента:
.
Если , то основная гипотеза принимается.
Если , то основную гипотезу отвергают.
Случай 3:
альтернативная гипотеза
< a. В этом случае
строится левосторонняя критическая
область. Критическая точка
.
Если , то основная гипотеза принимается.
Если , то основную гипотезу отвергают.
96. В
ряде экспериментов исследовалось
влияние CaO как активатора
расширения ангидритовых растворов.
Было изготовлено две серии пробных
образцов по 6 штук каждая. Серия 0 (нулевая
проба) не содержала CaO;
серия 1 содержала 1% CaO. По
результатам исследований получено:
;
;
,
т. е. имеются точечные оценки параметров
двух случайных величин: 0
– расширения раствора, не содержащего
CaO, и 1
– расширения раствора, содержащего
CaO.
Выясним, значимо ли различие между обоими средними. Для этого проверим гипотезу M0 M1 при уровне значимости 0,05 и альтернативной гипотезе M0 M1.
Так как обе выборки
имеют малый объем, то сначала нужно
проверить гипотезу о равенстве их
дисперсий. В этом случае воспользуемся
односторонним критерием, так что
конкурирующая гипотеза будет иметь
вид: D
> D
По таблице критических точек распределения
Фишера по уровню значимости 0,05
и числам степеней свободы
находим
.
Так как
,
то исправленные выборочные дисперсии
отличаются незначимо. Далее вычисляем
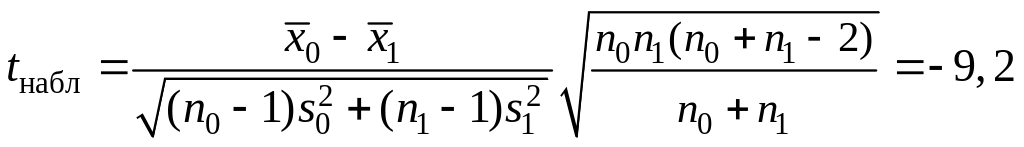и по таблице критических точек
распределения Стьюдента по уровню
значимости a / 2
0,025 и числу степеней свободы
получаем
.
Так как
,
то основная гипотеза отвергается,
другими словами, различие между средними
значимо. Таким образом, влияние CaO
как активатора расширения ангидритовых
растворов существенно.
97. Разрушающая
нагрузка, которой подвергается после
тепловой обработки бетонное покрытие
здания, должна составлять 2,0 кН. По
результатам исследования выборочной
совокупности объема n
= 6 имеем:
кН;
s = 0,112кН. Определить,
значимо ли различие между
и
ожидаемой величиной
кН при уровне значимости 0,05
.
Для этого проверим гипотезу M 2 при уровне значимости 0,05 и альтернативной гипотезе M < 2. Так как выборка имеет малый объем, для проверки этой гипотезы воспользуемся критерием .
Тогда
и по таблице критических точек
распределения Стьюдента по уровню
значимости a
0,05 и числу степеней свободы
получаем
.
Поэтому, так как
и следовательно,
то
,
то есть основная гипотеза принимается.
Другими словами, различие между
и
ожидаемой величиной
кН незначимо.
Для двух независимых выборок, извлеченных из нормальных генеральных совокупностей при уровне значимости = 0,05 проверить основную гипотезу H0: D = D при конкурирующей гипотезе H1: D > D. Если эта гипотеза принимается, то при уровне значимости = 0,05 проверить основную гипотезу H0: M = M при конкурирующей гипотезе H1: M M.
98. |
: |
14 |
12 |
14 |
15 |
7 |
19 |
14 |
12 |
12 |
6 |
|
|
|
: |
13 |
6 |
15 |
13 |
11 |
13 |
16 |
17 |
13 |
6 |
12 |
10 |
99. |
: |
10 |
6 |
9 |
16 |
16 |
12 |
16 |
15 |
17 |
10 |
|
|
|
: |
15 |
13 |
10 |
10 |
15 |
14 |
16 |
10 |
5 |
14 |
15 |
12 |
100. |
: |
12 |
12 |
4 |
14 |
17 |
12 |
12 |
10 |
16 |
11 |
|
|
: |
13 |
14 |
15 |
16 |
11 |
9 |
19 |
15 |
11 |
11 |
9 |
14 |
101. |
: |
13 |
15 |
14 |
12 |
14 |
14 |
16 |
12 |
3 |
15 |
|
|
|
: |
14 |
13 |
17 |
12 |
11 |
13 |
6 |
15 |
17 |
15 |
12 |
13 |
102. |
ξ: |
13 |
16 |
17 |
16 |
12 |
17 |
16 |
15 |
13 |
13 |
|
|
|
: |
16 |
16 |
12 |
16 |
16 |
15 |
13 |
14 |
17 |
10 |
11 |
13 |
103. |
ξ: |
14 |
13 |
16 |
11 |
12 |
11 |
8 |
12 |
10 |
16 |
|
|
η: |
15 |
14 |
10 |
16 |
15 |
18 |
18 |
14 |
7 |
11 |
8 |
104. |
ξ: |
17 |
16 |
16 |
16 |
12 |
16 |
15 |
13 |
17 |
15 |
|
|
η: |
17 |
13 |
12 |
14 |
16 |
17 |
15 |
14 |
15 |
10 |
11 |
15 |
105. |
: |
16 |
16 |
10 |
16 |
17 |
14 |
16 |
16 |
16 |
14 |
|
|
: |
16 |
18 |
16 |
14 |
17 |
15 |
14 |
13 |
12 |
13 |
9 |
11 |
106. |
: |
8 |
6 |
2 |
3 |
1 |
5 |
4 |
6 |
7 |
5 |
|
|
: |
9 |
13 |
16 |
12 |
14 |
7 |
15 |
12 |
16 |
14 |
8 |
7 |
107. |
: |
10 |
16 |
18 |
14 |
15 |
17 |
16 |
12 |
13 |
12 |
|
|
: |
12 |
16 |
19 |
16 |
13 |
15 |
16 |
13 |
16 |
17 |
11 |
12 |
108. |
: |
–4 |
–6 |
–1 |
–5 |
1 |
–2 |
1 |
7 |
1 |
– 2 |
|
|
: |
– 6 |
– 1 |
3 |
– 4 |
1 |
– 1 |
– 4 |
– 5 |
3 |
– 2 |
4 |
3 |
109. |
: |
4 |
2 |
6 |
5 |
4 |
6 |
3 |
7 |
5 |
8 |
|
|
: |
3 |
6 |
9 |
1 |
6 |
5 |
9 |
3 |
9 |
12 |
2 |
5 |
110. |
: |
17 |
18 |
19 |
10 |
21 |
17 |
18 |
19 |
10 |
21 |
|
|
: |
21 |
19 |
25 |
13 |
17 |
21 |
19 |
25 |
13 |
17 |
18 |
12 |
111. |
: |
33 |
34 |
44 |
42 |
35 |
46 |
36 |
44 |
35 |
44 |
|
|
: |
30 |
34 |
38 |
41 |
36 |
40 |
47 |
46 |
47 |
38 |
41 |
36 |
112. |
: |
32 |
36 |
36 |
31 |
49 |
38 |
47 |
43 |
51 |
48 |
|
|
: |
45 |
39 |
52 |
43 |
44 |
35 |
50 |
44 |
49 |
54 |
52 |
44 |
113. |
: |
44 |
38 |
41 |
49 |
48 |
34 |
46 |
47 |
35 |
42 |
|
|
: |
49 |
39 |
42 |
49 |
46 |
38 |
41 |
48 |
43 |
31 |
42 |
41 |
114. |
: |
32 |
36 |
36 |
31 |
49 |
38 |
47 |
43 |
51 |
48 |
|
|
: |
39 |
34 |
45 |
36 |
39 |
34 |
43 |
41 |
45 |
43 |
44 |
41 |
115. |
: |
38 |
41 |
49 |
48 |
34 |
46 |
47 |
55 |
32 |
46 |
|
|
: |
42 |
48 |
50 |
49 |
41 |
33 |
48 |
48 |
49 |
36 |
33 |
36 |
116. |
: |
38 |
38 |
42 |
42 |
50 |
41 |
42 |
41 |
44 |
41 |
|
|
: |
41 |
40 |
46 |
41 |
49 |
43 |
43 |
41 |
38 |
43 |
43 |
48 |
117. |
: |
52 |
56 |
58 |
55 |
67 |
70 |
63 |
64 |
68 |
62 |
|
|
: |
73 |
70 |
66 |
61 |
64 |
54 |
64 |
73 |
61 |
75 |
73 |
70 |
118. |
: |
65 |
51 |
57 |
68 |
53 |
67 |
61 |
58 |
61 |
54 |
|
|
: |
58 |
55 |
67 |
68 |
66 |
67 |
67 |
70 |
50 |
51 |
53 |
50 |
119. |
: |
64 |
68 |
54 |
68 |
74 |
73 |
65 |
67 |
51 |
56 |
|
|
: |
68 |
69 |
70 |
70 |
54 |
67 |
64 |
60 |
58 |
69 |
67 |
70 |
120. |
: |
46 |
39 |
44 |
41 |
49 |
39 |
40 |
43 |
44 |
43 |
|
|
: |
42 |
37 |
42 |
46 |
53 |
45 |
35 |
46 |
42 |
42 |
43 |
40 |
121. |
: |
37 |
40 |
41 |
39 |
36 |
40 |
42 |
39 |
40 |
36 |
|
|
: |
40 |
35 |
38 |
39 |
42 |
42 |
39 |
38 |
36 |
41 |
35 |
33 |
122. |
: |
17 |
14 |
16 |
14 |
18 |
20 |
18 |
18 |
10 |
20 |
|
|
: |
14 |
17 |
15 |
18 |
23 |
18 |
18 |
18 |
10 |
17 |
20 |
15 |
123. |
: |
19 |
18 |
21 |
23 |
17 |
17 |
18 |
19 |
10 |
21 |
|
|
: |
24 |
20 |
21 |
46 |
18 |
20 |
19 |
21 |
13 |
22 |
23 |
20 |
124. |
: |
42 |
37 |
39 |
39 |
42 |
41 |
44 |
38 |
38 |
46 |
|
|
: |
37 |
37 |
46 |
42 |
47 |
42 |
44 |
34 |
45 |
44 |
45 |
40 |
125. |
: |
14 |
5 |
4 |
5 |
9 |
3 |
4 |
4 |
4 |
3 |
|
|
: |
14 |
4 |
15 |
4 |
17 |
14 |
20 |
19 |
21 |
19 |
13 |
20 |
126. |
: |
52 |
56 |
58 |
55 |
67 |
70 |
63 |
64 |
68 |
62 |
|
|
: |
54 |
64 |
55 |
54 |
57 |
64 |
70 |
69 |
61 |
59 |
63 |
60 |
127. |
: |
3 |
10 |
6 |
6 |
6 |
3 |
6 |
3 |
4 |
5 |
|
|
: |
6 |
5 |
4 |
4 |
10 |
5 |
7 |
2 |
2 |
5 |
7 |
9 |
128. |
: |
41 |
34 |
36 |
37 |
36 |
34 |
43 |
33 |
31 |
40 |
|
|
: |
42 |
35 |
42 |
34 |
39 |
43 |
40 |
41 |
33 |
45 |
43 |
41 |
129. |
: |
7 |
5 |
4 |
7 |
3 |
10 |
2 |
2 |
6 |
4 |
|
|
: |
2 |
6 |
4 |
9 |
4 |
5 |
10 |
3 |
4 |
6 |
3 |
7 |
130. |
: |
5 |
4 |
2 |
2 |
6 |
4 |
– 1 |
0 |
4 |
– 2 |
|
|
: |
– 1 |
4 |
4 |
4 |
10 |
8 |
– 2 |
4 |
6 |
2 |
3 |
0 |
131. |
: |
3 |
6 |
6 |
– 3 |
– 1 |
2 |
6 |
8 |
4 |
11 |
|
|
: |
– 1 |
– 1 |
– 1 |
5 |
3 |
9 |
0 |
12 |
11 |
3 |
6 |
5 |
132. |
: |
3 |
3 |
3 |
4 |
1 |
9 |
2 |
7 |
4 |
6 |
|
|
: |
3 |
10 |
6 |
1 |
4 |
4 |
6 |
7 |
6 |
5 |
7 |
3 |
133. |
: |
10 |
13 |
11 |
6 |
18 |
13 |
12 |
22 |
14 |
18 |
|
|
: |
10 |
20 |
16 |
17 |
22 |
17 |
14 |
15 |
13 |
17 |
16 |
14 |
134. |
: |
14 |
21 |
19 |
19 |
25 |
20 |
15 |
23 |
23 |
19 |
|
|
: |
15 |
25 |
21 |
22 |
27 |
26 |
19 |
24 |
19 |
21 |
23 |
22 |
135. |
: |
8 |
11 |
9 |
4 |
12 |
8 |
8 |
15 |
12 |
14 |
|
|
: |
9 |
14 |
10 |
10 |
15 |
12 |
13 |
15 |
14 |
11 |
17 |
10 |
136. |
: |
16 |
24 |
18 |
17 |
24 |
18 |
14 |
15 |
13 |
19 |
|
|
: |
15 |
26 |
20 |
16 |
23 |
18 |
15 |
20 |
16 |
20 |
17 |
13 |
137. |
: |
20 |
22 |
21 |
17 |
12 |
10 |
18 |
23 |
23 |
22 |
|
|
: |
18 |
10 |
12 |
11 |
17 |
16 |
18 |
26 |
22 |
22 |
16 |
12 |
138. |
: |
3,9 |
3,7 |
3,2 |
3,9 |
4,0 |
3,6 |
3,8 |
3,6 |
4,0 |
3,9 |
|
|
: |
3,7 |
3,7 |
4,3 |
3,8 |
4,2 |
4,7 |
4,3 |
3,3 |
4,3 |
3,8 |
3,8 |
4,3 |
139. |
: |
4,6 |
3,8 |
4,2 |
3,8 |
4,7 |
4,0 |
4,3 |
4,6 |
4,2 |
4,0 |
|
|
: |
4,1 |
3,9 |
3,9 |
3,8 |
4,1 |
3,6 |
4,1 |
3,6 |
4,1 |
3,7 |
4,2 |
3,8 |
140. |
: |
18 |
18 |
18 |
16 |
15 |
20 |
19 |
21 |
20 |
23 |
|
|
: |
19 |
19 |
19 |
15 |
16 |
22 |
21 |
23 |
22 |
21 |
17 |
18 |
141. |
: |
17 |
17 |
20 |
19 |
17 |
22 |
18 |
22 |
19 |
18 |
|
|
: |
19 |
17 |
17 |
18 |
21 |
21 |
20 |
18 |
18 |
19 |
17 |
19 |
Для выборки объема n 14 (вторая строка таблицы п. 1), извлеченной из нормальной генеральной совокупности при уровне значимости = 0,05 проверить основную гипотезу H0: M a при конкурирующей гипотезе H1: < a.
142. Таблица из задачи 7. 143. Таблица из задачи 8.
144. Таблица из задачи 9. 145. Таблица из задачи 10.
146. Таблица из задачи 11. 147. Таблица из задачи 12.
148. Таблица из задачи 13. 149. Таблица из задачи 14.
150. Таблица из задачи 15. 151. Таблица из задачи 16.
152. Таблица из задачи 17. 153. Таблица из задачи 18.
154. Таблица из задачи 19. 155. Таблица из задачи 20.
156. Таблица из задачи 21. 157. Таблица из задачи 22.
158. Таблица из задачи 23. 159. Таблица из задачи 24.
160. Таблица из задачи 25. 161. Таблица из задачи 26.
162. Таблица из задачи 27. 163. Таблица из задачи 28.
164. Таблица из задачи 29. 165. Таблица из задачи 30.
166. Таблица из задачи 31. 167. Таблица из задачи 32.
168. Таблица из задачи 33. 169. Таблица из задачи 34.
170. Таблица из задачи 35. 171. Таблица из задачи 36.
172. Таблица из задачи 37. 173. Таблица из задачи 38.
174. Таблица из задачи 39. 175. Таблица из задачи 40.
176. Таблица из задачи 41. 177. Таблица из задачи 42.
178. Таблица из задачи 43. 179. Таблица из задачи 44.
180. Таблица из задачи 45. 181. Таблица из задачи 46.
182. Таблица из задачи 47. 183. Таблица из задачи 48.
184. Таблица из задачи 49. 185. Таблица из задачи 50.
1.4. Проверка
гипотезы о нормальном распределении
генеральной совокупности. Критерий
согласия Пирсона. Критерий для проверки
гипотезы о предполагаемом законе
неизвестного распределения называют
критерием согласия. Одним из критериев
согласия является критерий
Пирсона, который можно применять для
проверки различных гипотез о законе
распределения случайной величины. Для
построения критерия числовая прямая
разбивается на несколько промежутков
и устанавливается наблюдаемое и
теоретическое число значений случайной
величины, попадающее в каждый промежуток.
Рассмотрим применение критерия Пирсона для проверки гипотезы о нормальном распределении.
Пусть имеется выборка значений случайной величины объема n. Отрезок, концами которого являются наименьшая и наибольшая варианты, содержит все числа этой выборки. Разобьем этот отрезок на m частичных промежутков одинаковой длины:
[ y1; y2), [ y2; y3), [ y3; y4), ..., [ ym–1; ym), [ ym; ym+1]
(общие концы двух соседних промежутков отнесены к правому промежутку). Обозначим через nj – число элементов выборки, попавших в j-й промежуток (n1 + n2 + ... + nm n). Поскольку y1 и ym+1 – наименьшая и наибольшая варианты, то крайние промежутки данной последовательности можно заменить промежутками (–; y2) и [ym; ), не меняя значений n1 и nm. Таким образом, мы получаем последовательность промежутков
(–; y2), [ y2; y3), [ y3; y4), ..., [ym–1; ym), [ym; ),
объединение
которых – вся числовая прямая. При этом
n1, n2,
..., nm
являются количествами чисел имеющейся
выборки, попавшими в эти промежутки.
Наряду с этими наблюдаемыми количествами
можно построить теоретические в
предположении, что случайная величина
распределена по
нормальному закону. Для этого введем в
рассмотрение числа
(середины промежутков данной
последовательности). Эти числа называют
равноотстоящими вариантами, полученными
группировкой выборки. Приписывая им
в качестве кратностей числа nj,
получим следующий закон распределения
|
|
... |
|
|
|
... |
|
Математическим ожиданием и дисперсией этого распределения являются числа
,
,
которые
называют выборочными математическим
ожиданием и дисперсией, полученными
группировкой выборки. При большом n
эти числа мало отличаются от
и
.
Рассматривая числа
и
как приближенные значения математического
ожидания и квадратичного отклонения
случайной величины
и предполагая, что эта случайная величина
распределена по нормальному закону,
найдем вероятности того, что ее значения
попадают в данные промежутки.
;
при j 2, 3, ..., m – 1;
,
где
;
.
Теоретические
кратности находят по формуле:
.
Рассмотрим теперь случайную величину
,
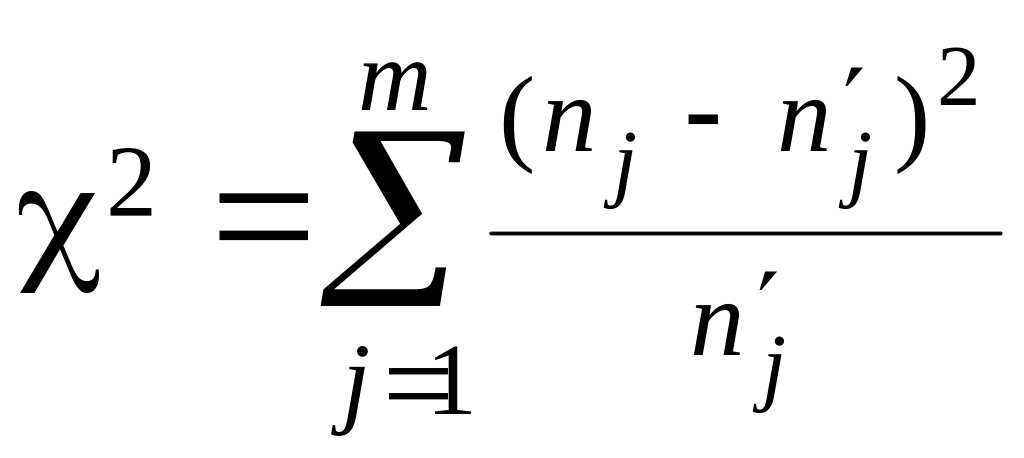которая, как доказал Пирсон, распределена по закону 2 c m – 3 степенями свободы.
Ее можно использовать для проверки гипотезы о нормальном распределении данной случайной величины .
Построим
правостороннюю критическую область,
исходя из требования, чтобы вероятность
попадания значения критерия в эту
область в предположении справедливости
основной гипотезы равнялась принятому
уровню значимости .
Критическая точка
удовлетворяет условию
и находится по таблице критических
точек распределения 2.
Если
,
то основную гипотезу принимают.
Если
,
то нулевую гипотезу отвергают.
186. Получена выборка значений случайной величины объема n 190. Найденные значения распределены по промежуткам следующим образом.
Промежуток |
[4; 6) |
[6; 8) |
[8; 10) |
[10; 12) |
[12; 14) |
Количество |
n1 15 |
n2 26 |
n3 25 |
n4 30 |
n5 26 |
Промежуток |
[14; 16) |
[16; 18) |
[18; 20) |
[20; 22] |
Количество |
n6 14 |
n7 16 |
n8 18 |
n9 20 |
Проверим гипотезу о нормальном распределении .
Находим равноотстоящие варианты:
,
,
,
,
,
,
,
,
.
По формулам (8) получаем 12,6, 4,93.
Вычисление чисел
проведено с помощью расчетной таблицы,
приведенной на стр. 72.
j |
yj |
|
(zj) |
pj (zj+1) – (zj) |
190pj |
1 |
– |
– |
–0,5 |
0,0901 |
17,119 |
2 |
6 |
– 1,34 |
–0,4099 |
0,0861 |
16,359 |
3 |
8 |
– 0,93 |
–0,3238 |
0,1219 |
23,161 |
4 |
10 |
– 0,53 |
–0,2019 |
0,1541 |
29,279 |
5 |
12 |
– 0,12 |
–0,0478 |
0,1581 |
30,039 |
6 |
14 |
0,28 |
0,1103 |
0,1446 |
27,474 |
7 |
16 |
0,69 |
0,2549 |
0,1094 |
20,786 |
8 |
18 |
1,10 |
0,3643 |
0,0689 |
13,091 |
9 |
20 |
1,50 |
0,4332 |
0,0668 |
12,692 |
10 |
|
|
0,5 |
|
|
|
|
Контроль: |
|
|
|
Отсюда следует
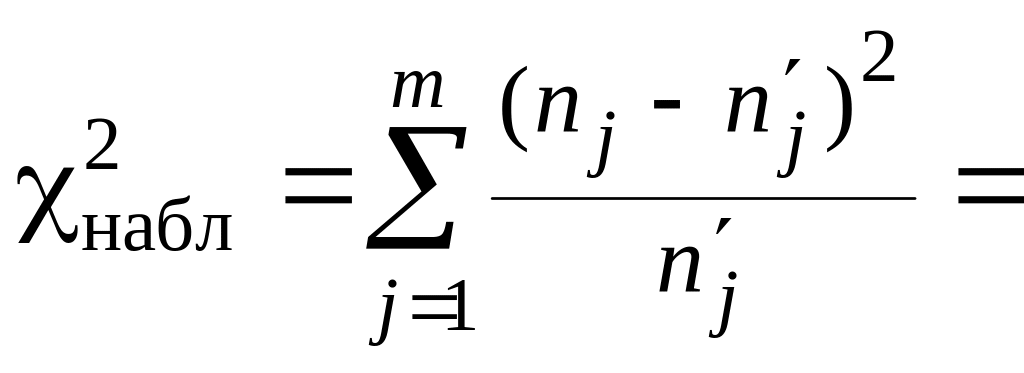20,41,
а по таблице критических точек
распределения 2
(табл. 3) находим
.
Так как
,
гипотеза о нормальном распределении
отвергается.
Для выборок значений случайной величины из §1 объема n 100 проверить гипотезу о нормальном распределении .
187. Таблица из задачи 7. 188. Таблица из задачи 8.
189. Таблица из задачи 9. 190. Таблица из задачи 10.
191. Таблица из задачи 11. 192. Таблица из задачи 12.
193. Таблица из задачи 13. 194. Таблица из задачи 14.
195. Таблица из задачи 15. 196. Таблица из задачи 16.
197. Таблица из задачи 17. 198. Таблица из задачи 18.
199. Таблица из задачи 19. 200. Таблица из задачи 20.
201. Таблица из задачи 21. 202. Таблица из задачи 22.
203. Таблица из задачи 23. 204. Таблица из задачи 24.
205. Таблица из задачи 25. 206. Таблица из задачи 26.
207. Таблица из задачи 27. 208. Таблица из задачи 28.
209. Таблица из задачи 29. 210. Таблица из задачи 30.
211. Таблица из задачи 31. 212. Таблица из задачи 32.
213. Таблица из задачи 33. 214. Таблица из задачи 34.
215. Таблица из задачи 35. 216. Таблица из задачи 36.
217. Таблица из задачи 37. 218. Таблица из задачи 38.
219. Таблица из задачи 39. 220. Таблица из задачи 40.
221. Таблица из задачи 41. 222. Таблица из задачи 42.
223. Таблица из задачи 43. 224. Таблица из задачи 44.
225. Таблица из задачи 45. 226. Таблица из задачи 46.
227. Таблица из задачи 47. 228. Таблица из задачи 48.
229. Таблица из задачи 49. 230. Таблица из задачи 50.
1.5. Однофакторный
дисперсионный анализ. Пусть случайные
величины 1,
2,
..., p
распределены по нормальному закону и
имеют одинаковую и притом неизвестную
дисперсию 2,
математические ожидания также неизвестны,
но могут быть различными. Требуется при
заданном уровне значимости проверить
гипотезу
о равенстве всех математических
ожиданий: M1
M2
...
Mp.
Для этого используется метод, основанный
на сравнении некоторых дисперсий и
поэтому названный дисперсионным
анализом.
Основная идея дисперсионного анализа состоит в сравнении факторной дисперсии, порождаемой воздействием фактора, с остаточной дисперсией, обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на изучаемую величину .
Пусть на количественный признак, значение которого есть нормально распределенная случайная величина, воздействует фактор F, имеющий p постоянных уровней. Пусть проведена группа из q1 испытаний при уровне F1, группа из q2 испытаний при уровне F2, ..., группа из qp испытаний при уровне Fp. Обозначив через xij значение, полученное в i-м испытании при j-м уровне, имеем следующую таблицу результатов.
i (номер испы- тания) |
Уровни фактора |
|||
|
|
... |
|
|
1 |
x11 |
x12 |
... |
x1p |
2 |
x21 |
x22 |
... |
x2p |
… |
... |
... |
... |
... |
q1 |
|
… |
... |
… |
... |
|
... |
... |
... |
q2 |
|
|
... |
... |
... |
|
|
... |
... |
qp |
|
|
... |
|
Групповая средняя |
|
|
... |
|
Пусть
,
где
,
т. е.
– общее среднее всех xij.
Введем в рассмотрение суммы:
– общая сумма,
– факторная
сумма,
– остаточная
сумма.
Общая сумма является суммой квадратов отклонений наблюдаемых значений от общей средней, факторная сумма есть сумма квадратов отклонений групповых средних от общей средней, остаточная сумма представляет собой сумму квадратов отклонений наблюдаемых значений от своей групповой средней.
Выполняется равенство Sобщ Sфакт + Sост.
Выражения для
общей и факторной сумм можно привести
к виду, более удобному для вычислений.
Для этого введем обозначения:
,
.
Используя эти обозначения, получаем формулы
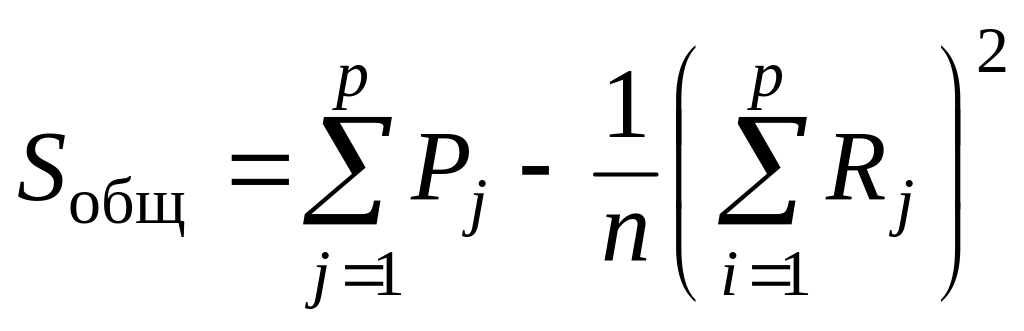и
.
Величины
,
,
называют соответственно общей,
факторной и остаточной дисперсиями.
Пусть случайные
величины
,
,...,
распределены по нормальному закону и
имеют одинаковую неизвестную дисперсию
2,
математические ожидания также неизвестны,
но могут быть различными. Построим
критерий для проверки при заданном
уровне значимости гипотезы
:
M1
M2
...
Mp
.
Случайная величина
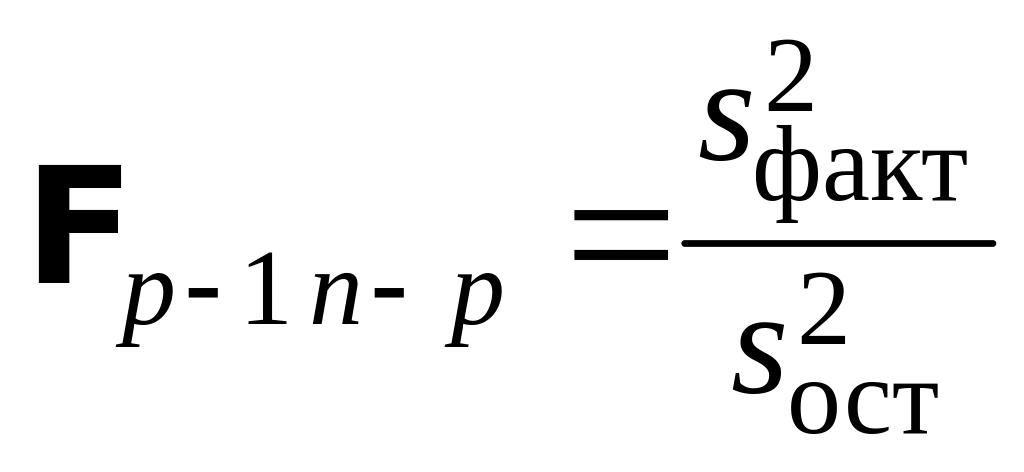распределена (при условии справедливости
гипотезы H0) по
закону Фишера со степенями свободы p
– 1 и n – p.
Эта случайная величина и является
критерием для рассматриваемой гипотезы.
Решение задачи сводится к сравнению факторной и остаточной дисперсий по критерию Фишера.
Вычисляют
и, если Fнабл
окажется больше Fкр
то гипотеза о равенстве групповых
математических ожиданий должна быть
отвергнута. Если же окажется Fнабл<
Fкр,
гипотеза
принимается.
Если факторная дисперсия окажется меньше остаточной, то отсюда сразу следует справедливость гипотезы о равенстве групповых математических ожиданий, т. е. нет необходимости применять критерий Фишера.
231. Пусть произведено 14 испытаний на различных уровнях фактора F: 5 испытаний на уровне F1, 3 испытания на уровне F2, 2 испытания на уровне F3 и 4 испытания на уровне F4. Результаты испытаний представлены следующей таблицей.
i (номер ис- пытания) |
Уровни фактора |
|||
|
|
F3 |
F4 |
|
1 |
1,5 |
3,3 |
5,6 |
6,1 |
2 |
2,1 |
3,1 |
4,8 |
5,9 |
3 |
1,4 |
4,5 |
|
4,7 |
4 |
2,2 |
|
|
4,3 |
5 |
2,4 |
|
|
|
Требуется проверить на уровне значимости 0,05 гипотезу о равенстве математических ожиданий нормально распределенных случайных величин 1, 2, 3, 4, возникающих при различных уровнях фактора F. Предполагается, что дисперсии этих случайных величин одинаковы. Обозначим через xij значение, полученное в i-м испытании при j-м уровне фактора, и составим расчетную таблицу.
i |
|
|
|
|
|
|
|
|
1 |
1,5 |
3,3 |
5,6 |
6,1 |
2,25 |
10,89 |
31,36 |
37,21 |
2 |
2,1 |
3,1 |
4,8 |
5,9 |
4,41 |
9,61 |
23,04 |
34,81 |
3 |
1,4 |
4,5 |
|
4,7 |
1,96 |
20,25 |
|
22,09 |
4 |
2,2 |
|
|
4,3 |
4,84 |
|
|
18,49 |
5 |
2,4 |
|
|
|
5,76 |
|
|
|
Rj |
9,6 |
10,9 |
10,4 |
21,0 |
|
|
|
|
Pj |
|
|
|
|
19,22 |
40,75 |
54,40 |
112,60 |
|
92,16 |
118,81 |
108,16 |
441 |
|
|
|
|
Отсюда
;
;
.
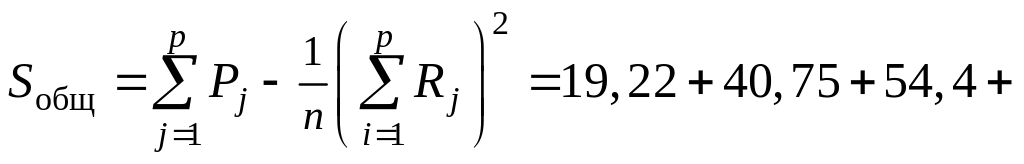
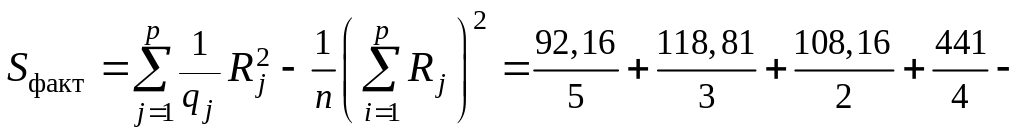
Далее найдем
факторную и остаточную дисперсии:
;
.
Получаем Fнабл
=
.
По таблице критических точек распределения
Фишера находим Fкр
= 3,71. Так как Fнабл
> Fкр,
гипотеза
отвергается.
Произведено по ki испытания на каждом из p уровней фактора F. В следующих задачах проверить основную гипотезу о равенстве математических ожиданий нормально распределенных случайных величин 1, 2, 3, …, p, возникающих при различных уровнях фактора F. Предполагается, что дисперсии этих случайных величин одинаковы.
232. |
i |
F1 |
F2 |
F3 |
F4 |
|
|
|
233. |
i |
F1 |
F2 |
F3 |
F4 |
|
1 |
38 |
33 |
37 |
32 |
|
|
|
|
1 |
47 |
78 |
87 |
53 |
|
2 |
41 |
32 |
42 |
44 |
|
|
|
|
2 |
61 |
55 |
82 |
58 |
|
3 |
39 |
35 |
44 |
48 |
|
|
|
|
3 |
79 |
69 |
84 |
64 |
|
4 |
36 |
33 |
48 |
51 |
|
|
|
|
4 |
66 |
77 |
81 |
61 |
234. |
i |
F1 |
F2 |
F3 |
F4 |
|
|
|
235. |
i |
F1 |
F2 |
F3 |
F4 |
|
1 |
15 |
25 |
24 |
22 |
|
|
|
|
1 |
12 |
11 |
17 |
12 |
|
2 |
23 |
18 |
32 |
17 |
|
|
|
|
2 |
15 |
8 |
25 |
14 |
|
3 |
37 |
16 |
29 |
26 |
|
|
|
|
3 |
8 |
13 |
29 |
22 |
|
4 |
34 |
19 |
38 |
33 |
|
|
|
|
4 |
23 |
11 |
22 |
10 |
236. |
i |
F1 |
F2 |
F3 |
F4 |
|
|
|
237. |
i |
F1 |
F2 |
F3 |
F4 |
|
1 |
38 |
33 |
37 |
32 |
|
|
|
|
1 |
38 |
33 |
37 |
32 |
|
2 |
41 |
32 |
42 |
44 |
|
|
|
|
2 |
41 |
32 |
42 |
44 |
|
3 |
39 |
35 |
44 |
48 |
|
|
|
|
3 |
39 |
35 |
44 |
48 |
|
4 |
36 |
33 |
48 |
51 |
|
|
|
|
4 |
36 |
33 |
48 |
51 |
238. |
i |
F1 |
F2 |
F3 |
F4 |
|
|
|
239. |
i |
F1 |
F2 |
F3 |
F4 |
|
1 |
42 |
67 |
76 |
78 |
|
|
|
|
1 |
29 |
19 |
33 |
20 |
|
2 |
76 |
54 |
71 |
64 |
|
|
|
|
2 |
48 |
45 |
22 |
28 |
|
3 |
55 |
34 |
82 |
60 |
|
|
|
|
3 |
33 |
23 |
35 |
38 |
|
4 |
74 |
65 |
57 |
77 |
|
|
|
|
4 |
21 |
32 |
20 |
32 |
240. |
i |
F1 |
F2 |
F3 |
F4 |
|
|
|
241. |
i |
F1 |
F2 |
F3 |
F4 |
|
1 |
64 |
47 |
79 |
55 |
|
|
|
|
1 |
43 |
54 |
87 |
92 |
|
2 |
61 |
40 |
88 |
60 |
|
|
|
|
2 |
38 |
61 |
81 |
99 |
|
3 |
54 |
51 |
91 |
51 |
|
|
|
|
3 |
34 |
59 |
85 |
93 |
|
4 |
76 |
61 |
86 |
49 |
|
|
|
|
4 |
42 |
55 |
83 |
94 |
242. |
i |
F1 |
F2 |
F3 |
F4 |
|
|
|
243. |
i |
F1 |
F2 |
F3 |
F4 |
1 |
8 |
17 |
22 |
18 |
|
|
|
|
1 |
88 |
60 |
33 |
22 |
|
2 |
9 |
13 |
19 |
23 |
|
|
|
|
2 |
79 |
59 |
42 |
30 |
|
3 |
2 |
16 |
20 |
22 |
|
|
|
|
3 |
75 |
69 |
31 |
29 |
|
4 |
6 |
11 |
23 |
27 |
|
|
|
|
4 |
82 |
61 |
44 |
24 |
244. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
245. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
38 |
33 |
37 |
32 |
29 |
1 |
47 |
78 |
87 |
53 |
48 |
||
2 |
41 |
32 |
42 |
44 |
34 |
2 |
61 |
55 |
82 |
58 |
51 |
||
3 |
39 |
35 |
44 |
48 |
32 |
3 |
79 |
69 |
84 |
64 |
49 |
||
4 |
36 |
33 |
48 |
51 |
28 |
4 |
66 |
77 |
81 |
61 |
54 |
||
5 |
35 |
31 |
46 |
42 |
31 |
5 |
64 |
73 |
84 |
62 |
58 |
246. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
247. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
15 |
25 |
24 |
22 |
33 |
1 |
12 |
11 |
17 |
12 |
21 |
||
2 |
23 |
18 |
32 |
17 |
38 |
2 |
15 |
8 |
25 |
14 |
18 |
||
3 |
37 |
16 |
29 |
26 |
36 |
3 |
8 |
13 |
29 |
22 |
26 |
||
4 |
34 |
19 |
38 |
33 |
29 |
4 |
23 |
11 |
22 |
10 |
15 |
||
5 |
28 |
23 |
32 |
35 |
30 |
5 |
18 |
5 |
15 |
18 |
30 |
248. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
249. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
38 |
33 |
37 |
32 |
40 |
1 |
38 |
33 |
37 |
32 |
29 |
||
2 |
41 |
32 |
42 |
44 |
44 |
2 |
41 |
32 |
42 |
44 |
33 |
||
3 |
39 |
35 |
44 |
48 |
42 |
3 |
39 |
35 |
44 |
48 |
37 |
||
4 |
36 |
33 |
48 |
51 |
49 |
4 |
36 |
33 |
48 |
51 |
41 |
||
5 |
43 |
31 |
45 |
49 |
52 |
5 |
42 |
38 |
39 |
42 |
31 |
250. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
251. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
38 |
33 |
37 |
32 |
29 |
1 |
37 |
33 |
37 |
32 |
29 |
||
2 |
41 |
32 |
42 |
44 |
33 |
2 |
40 |
30 |
42 |
44 |
34 |
||
3 |
39 |
35 |
44 |
48 |
37 |
3 |
39 |
35 |
44 |
48 |
32 |
||
4 |
36 |
33 |
48 |
51 |
41 |
4 |
36 |
33 |
48 |
51 |
28 |
||
5 |
42 |
38 |
39 |
42 |
31 |
5 |
35 |
31 |
46 |
42 |
31 |
252. |
i |
|
|
|
|
|
253. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
45 |
77 |
87 |
53 |
50 |
1 |
10 |
25 |
25 |
22 |
35 |
||
2 |
61 |
55 |
82 |
58 |
51 |
2 |
23 |
18 |
32 |
17 |
38 |
||
3 |
79 |
69 |
84 |
64 |
48 |
3 |
37 |
17 |
29 |
26 |
36 |
||
4 |
66 |
77 |
81 |
61 |
54 |
4 |
34 |
19 |
38 |
33 |
29 |
||
5 |
65 |
73 |
84 |
62 |
58 |
5 |
21 |
23 |
32 |
35 |
36 |
254. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
255. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
15 |
8 |
25 |
14 |
18 |
1 |
37 |
36 |
37 |
32 |
40 |
||
2 |
10 |
10 |
22 |
14 |
18 |
2 |
41 |
32 |
42 |
44 |
44 |
||
3 |
8 |
13 |
29 |
28 |
26 |
3 |
69 |
35 |
44 |
48 |
42 |
||
4 |
23 |
11 |
22 |
11 |
15 |
4 |
36 |
33 |
45 |
51 |
49 |
||
5 |
20 |
5 |
15 |
18 |
30 |
5 |
44 |
31 |
45 |
49 |
52 |
256. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
257. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
41 |
32 |
42 |
44 |
33 |
1 |
28 |
23 |
38 |
32 |
39 |
||
2 |
39 |
35 |
44 |
48 |
37 |
2 |
31 |
22 |
41 |
44 |
34 |
||
3 |
36 |
33 |
48 |
51 |
41 |
3 |
49 |
25 |
42 |
48 |
32 |
||
4 |
44 |
31 |
45 |
49 |
52 |
4 |
39 |
23 |
46 |
41 |
28 |
||
5 |
42 |
38 |
39 |
42 |
31 |
5 |
36 |
21 |
44 |
42 |
31 |
258. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
259. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
45 |
68 |
77 |
53 |
48 |
1 |
14 |
23 |
36 |
21 |
33 |
||
2 |
49 |
65 |
72 |
58 |
51 |
2 |
25 |
17 |
35 |
19 |
38 |
||
3 |
51 |
69 |
74 |
54 |
49 |
3 |
33 |
19 |
29 |
27 |
36 |
||
4 |
56 |
67 |
71 |
51 |
54 |
4 |
34 |
20 |
31 |
32 |
39 |
||
5 |
54 |
63 |
74 |
52 |
58 |
5 |
24 |
26 |
38 |
35 |
30 |
260. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
261. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
11 |
12 |
19 |
16 |
22 |
1 |
58 |
32 |
47 |
42 |
30 |
||
2 |
19 |
9 |
28 |
18 |
18 |
2 |
61 |
38 |
52 |
44 |
34 |
||
3 |
18 |
13 |
27 |
26 |
26 |
3 |
59 |
35 |
54 |
48 |
32 |
||
4 |
22 |
14 |
24 |
17 |
15 |
4 |
56 |
33 |
58 |
51 |
39 |
||
5 |
14 |
8 |
15 |
18 |
30 |
5 |
53 |
34 |
55 |
49 |
42 |
262. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
263. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
44 |
33 |
37 |
32 |
51 |
1 |
97 |
73 |
87 |
92 |
89 |
||
2 |
41 |
38 |
42 |
44 |
53 |
2 |
90 |
70 |
82 |
94 |
74 |
||
3 |
49 |
37 |
44 |
48 |
50 |
3 |
89 |
75 |
84 |
98 |
72 |
||
4 |
36 |
31 |
48 |
51 |
49 |
4 |
86 |
73 |
88 |
91 |
68 |
||
5 |
42 |
38 |
39 |
42 |
51 |
5 |
85 |
71 |
86 |
92 |
71 |
264. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
265. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
55 |
79 |
87 |
54 |
57 |
1 |
12 |
28 |
29 |
28 |
31 |
||
2 |
66 |
75 |
83 |
58 |
54 |
2 |
28 |
18 |
32 |
25 |
38 |
||
3 |
69 |
69 |
84 |
64 |
49 |
3 |
34 |
17 |
27 |
26 |
36 |
||
4 |
67 |
77 |
81 |
61 |
59 |
4 |
39 |
16 |
35 |
33 |
29 |
||
5 |
65 |
74 |
84 |
63 |
58 |
5 |
22 |
27 |
32 |
35 |
36 |
266. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
267. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
11 |
9 |
26 |
17 |
19 |
1 |
57 |
46 |
47 |
52 |
42 |
||
2 |
10 |
15 |
22 |
14 |
18 |
2 |
61 |
42 |
42 |
48 |
44 |
||
3 |
18 |
13 |
29 |
28 |
26 |
3 |
69 |
55 |
54 |
47 |
42 |
||
4 |
21 |
11 |
22 |
11 |
15 |
4 |
46 |
43 |
45 |
51 |
49 |
||
5 |
20 |
7 |
15 |
12 |
31 |
5 |
44 |
41 |
55 |
49 |
52 |
268. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
269. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
21 |
12 |
22 |
24 |
13 |
1 |
53 |
43 |
49 |
57 |
43 |
||
2 |
19 |
15 |
24 |
28 |
17 |
2 |
66 |
42 |
45 |
48 |
41 |
||
3 |
16 |
13 |
28 |
31 |
21 |
3 |
63 |
55 |
54 |
44 |
40 |
||
4 |
24 |
11 |
25 |
29 |
32 |
4 |
56 |
43 |
45 |
53 |
47 |
||
5 |
22 |
18 |
19 |
22 |
11 |
5 |
44 |
44 |
58 |
48 |
50 |
270 |
i |
F1 |
F2 |
F3 |
F4 |
|
271. |
i |
F1 |
F2 |
F3 |
F4 |
|
1 |
1,5 |
3,3 |
5,6 |
6,1 |
7,3 |
1 |
4,9 |
4,3 |
5,8 |
6,2 |
5,4 |
||
2 |
2,1 |
3,1 |
4,8 |
5,9 |
|
2 |
5,3 |
3,9 |
4,8 |
6,1 |
5,6 |
||
3 |
1,4 |
4,5 |
|
4,7 |
|
3 |
3,9 |
2,7 |
3,9 |
5,4 |
|
||
4 |
2,2 |
|
|
4,3 |
|
4 |
3,4 |
2,2 |
|
|
|
||
5 |
2,4 |
|
|
|
|
5 |
|
3,1 |
|
|
|
272. |
i |
F1 |
F2 |
F3 |
F4 |
|
273. |
i |
F1 |
F2 |
F3 |
F4 |
|
1 |
6,6 |
5,3 |
7,8 |
6,2 |
6,8 |
1 |
4,3 |
6,5 |
5,1 |
7,6 |
5,7 |
||
2 |
6,2 |
4,6 |
7,2 |
6,4 |
6,2 |
2 |
4,6 |
6,3 |
4,5 |
7,2 |
6,1 |
||
3 |
7,2 |
6,5 |
|
6,8 |
|
3 |
3,6 |
5,9 |
5,7 |
7,9 |
5,2 |
||
4 |
7,7 |
|
|
6,2 |
|
4 |
5,4 |
7,5 |
6,1 |
8,5 |
|
||
5 |
6,9 |
|
|
|
|
5 |
3,8 |
|
5,2 |
|
|
274 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
275. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,8 |
6,8 |
8,8 |
7,1 |
8,2 |
1 |
5,8 |
8,1 |
9,8 |
6,2 |
5,7 |
||
2 |
7,4 |
7,6 |
6,2 |
6,5 |
9,5 |
2 |
7,9 |
7,6 |
7,2 |
6,4 |
|
||
3 |
9,2 |
|
9,5 |
6,7 |
8,7 |
3 |
6,6 |
7,9 |
8,5 |
6,8 |
|
||
4 |
9,6 |
|
7,7 |
7,1 |
|
4 |
9,3 |
8,5 |
|
|
|
||
5 |
8,7 |
|
|
6,2 |
|
5 |
|
6,9 |
|
|
|
276 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
277. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,6 |
5,3 |
7,8 |
6,2 |
7,3 |
1 |
6,6 |
5,3 |
7,8 |
6,2 |
7,3 |
||
2 |
6,2 |
4,6 |
7,2 |
6,4 |
|
2 |
6,2 |
4,6 |
7,2 |
6,4 |
7,7 |
||
3 |
7,2 |
6,5 |
|
6,8 |
|
3 |
7,2 |
6,5 |
|
6,8 |
6,9 |
||
4 |
7,7 |
|
|
6,2 |
|
4 |
7,7 |
|
|
6,2 |
|
||
5 |
6,9 |
|
|
|
|
5 |
6,9 |
|
|
6,1 |
|
278 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
279. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,5 |
5,3 |
7,8 |
6,2 |
6,8 |
1 |
4,2 |
6,5 |
5,3 |
7,6 |
8,2 |
||
2 |
6,3 |
4,6 |
7,2 |
6,4 |
6,5 |
2 |
4,6 |
6,3 |
4,5 |
7,2 |
8,6 |
||
3 |
7,5 |
6,5 |
|
6,8 |
6,9 |
3 |
3,6 |
5,9 |
5,7 |
7,9 |
|
||
4 |
7,7 |
|
|
6,2 |
7,2 |
4 |
5,4 |
7,5 |
6,1 |
8,5 |
|
||
5 |
6,8 |
|
|
|
7,5 |
5 |
3,4 |
|
5,6 |
|
|
280 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
281. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,0 |
6,5 |
8,8 |
7,1 |
8,2 |
1 |
7,9 |
7,6 |
7,2 |
6,4 |
6,6 |
||
2 |
7,4 |
7,6 |
6,2 |
6,5 |
9,5 |
2 |
7,8 |
7,9 |
7,2 |
6,5 |
|
||
3 |
9,3 |
|
9,5 |
6,7 |
8,3 |
3 |
6,6 |
7,9 |
8,5 |
6,8 |
|
||
4 |
9,6 |
|
7,7 |
7,1 |
|
4 |
9,3 |
8,5 |
|
|
|
||
5 |
8,8 |
|
|
6,6 |
|
5 |
|
6,7 |
|
|
|
282 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
283. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,2 |
4,6 |
7,2 |
6,4 |
5,6 |
1 |
6,2 |
4,6 |
7,2 |
6,4 |
5,6 |
||
2 |
6,2 |
4,6 |
7,2 |
6,4 |
|
2 |
6,2 |
4,6 |
7,2 |
6,4 |
7,7 |
||
3 |
7,2 |
6,5 |
|
6,8 |
|
3 |
7,3 |
6,2 |
|
6,5 |
6,9 |
||
4 |
7,7 |
|
|
6,2 |
|
4 |
7,7 |
|
|
6,2 |
|
||
5 |
6,9 |
|
|
|
|
5 |
6,1 |
|
|
6,0 |
|
284 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
285. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,3 |
5,3 |
7,1 |
6,2 |
6,9 |
1 |
5,3 |
6,5 |
5,1 |
7,6 |
7,2 |
||
2 |
6,7 |
4,6 |
7,2 |
6,4 |
6,6 |
2 |
5,6 |
6,3 |
4,5 |
7,2 |
|
||
3 |
6,2 |
5,5 |
7,5 |
6,8 |
6,9 |
3 |
5,6 |
5,9 |
5,7 |
7,9 |
|
||
4 |
6,7 |
|
|
6,3 |
7,2 |
4 |
6,4 |
|
6,1 |
8,5 |
|
||
5 |
5,9 |
|
|
|
7,1 |
5 |
4,8 |
|
5,2 |
|
|
286 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
287. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,8 |
6,8 |
8,6 |
7,1 |
8,1 |
1 |
5,8 |
7,1 |
8,8 |
6,2 |
6,7 |
||
2 |
7,4 |
7,6 |
6,4 |
6,5 |
9,3 |
2 |
7,9 |
7,6 |
7,2 |
6,4 |
5,9 |
||
3 |
9,3 |
7,2 |
8,5 |
6,7 |
|
3 |
6,6 |
7,9 |
8,5 |
6,8 |
|
||
4 |
9,5 |
|
7,7 |
7,1 |
|
4 |
8,3 |
7,5 |
|
|
|
||
5 |
8,7 |
|
|
7,2 |
|
5 |
|
6,9 |
|
|
|
288 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
289. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,6 |
5,3 |
7,9 |
6,2 |
7,3 |
1 |
6,6 |
5,3 |
6,8 |
6,2 |
7,3 |
||
2 |
6,2 |
4,6 |
7,2 |
6,4 |
7,1 |
2 |
6,2 |
4,6 |
6,2 |
6,4 |
7,7 |
||
3 |
7,2 |
|
7,4 |
6,8 |
|
3 |
7,2 |
6,5 |
|
6,8 |
6,9 |
||
4 |
7,7 |
|
|
6,2 |
|
4 |
7,7 |
6,1 |
|
6,2 |
|
||
5 |
7,9 |
|
|
|
|
5 |
6,9 |
|
|
6,1 |
|
290 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
291. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
7,3 |
5,3 |
6,8 |
6,4 |
6,8 |
1 |
4,4 |
6,5 |
5,3 |
7,6 |
8,2 |
||
2 |
6,9 |
5,6 |
6,9 |
6,2 |
6,5 |
2 |
4,6 |
6,3 |
5,5 |
7,2 |
8,6 |
||
3 |
7,4 |
6,5 |
|
6,4 |
6,9 |
3 |
3,6 |
5,9 |
5,7 |
7,9 |
|
||
4 |
7,1 |
|
|
|
7,2 |
4 |
5,4 |
|
6,1 |
7,5 |
|
||
5 |
6,8 |
|
|
|
6,5 |
5 |
3,4 |
|
5,6 |
|
|
292 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
293. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,6 |
7,2 |
8,8 |
7,1 |
8,4 |
1 |
7,6 |
7,6 |
8,2 |
6,4 |
6,6 |
||
2 |
7,0 |
7,6 |
6,2 |
7,5 |
8,5 |
2 |
7,9 |
7,9 |
8,4 |
6,5 |
|
||
3 |
9,2 |
7,9 |
9,5 |
6,7 |
8,3 |
3 |
6,1 |
7,7 |
8,5 |
6,8 |
|
||
4 |
9,9 |
|
7,7 |
7,1 |
|
4 |
9,1 |
8,5 |
|
|
|
||
5 |
8,7 |
|
|
6,6 |
|
5 |
|
6,7 |
|
|
|
294 |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
295. |
i |
F1 |
F2 |
F3 |
F4 |
F5 |
1 |
6,8 |
5,6 |
7,2 |
6,6 |
5,6 |
1 |
8,1 |
7,6 |
7,2 |
6,4 |
8,6 |
||
2 |
6,1 |
4,6 |
7,4 |
6,4 |
5,3 |
2 |
9,3 |
7,6 |
7,1 |
6,8 |
7,7 |
||
3 |
7,2 |
6,5 |
|
6,8 |
|
3 |
7,3 |
6,2 |
8,5 |
6,5 |
8,9 |
||
4 |
7,7 |
5,1 |
|
|
|
4 |
7,7 |
|
|
6,2 |
|
||
5 |
6,9 |
|
|
|
|
5 |
8,1 |
|
|
6,3 |
|
§5. Элементы теории корреляции. Метод наименьших квадратов. Выборочное уравнение прямолинейной регрессии. Криволинейная регрессия. Пусть проведено n наблюдений, в результате которых получены следующие значения случайных величин , и .
Номер наблюдения |
1 |
2 |
... |
n |
Значение |
x1 |
x2 |
... |
xn |
Значение |
y1 |
y2 |
... |
yn |
Значение |
x1y1 |
x2y2 |
... |
xnyn |
Величины
,
и
есть точечные оценки соответственно
для M,
M
и M().
Величины
и
являются точечными оценками соответственно
для D
и D.
Поэтому в качестве точечной оценки
коэффициента корреляции
можно взять величину
.
Выборочное
уравнение линейной регрессии
по
имеет вид:
.
Аналогично
выборочное уравнение линейной регрессии
по
имеет вид:
.
Если
или
,
то эти уравнения эквивалентны.
296. Найти выборочный коэффициент корреляции случайных величин и по данным наблюдений.
Значения |
0,2 |
0,6 |
1,0 |
1,2 |
1,6 |
1,8 |
2,2 |
2,8 |
Значения |
0,2 |
0,4 |
1,0 |
1,2 |
1,4 |
1,8 |
0,8 |
1,0 |
Составим расчетную таблицу.
i |
xi |
yi |
|
|
xiyi |
1 |
0,2 |
0,2 |
0,04 |
0,04 |
0,04 |
2 |
0,6 |
0,4 |
0,36 |
0,16 |
0,24 |
3 |
1,0 |
1,0 |
1,00 |
1,00 |
1,00 |
4 |
1,2 |
1,2 |
1,44 |
1,44 |
1,44 |
5 |
1,6 |
1,4 |
2,56 |
1,96 |
2,24 |
6 |
1,8 |
1,8 |
3,24 |
3,24 |
3,24 |
7 |
2,2 |
0,8 |
4,84 |
0,64 |
1,76 |
8 |
2,8 |
1,0 |
7,84 |
1,00 |
2,80 |
|
11,4 |
7,8 |
21,32 |
9,48 |
12,76 |
/ n |
|
|
|
|
|
1,42
0,98
2,66
1,18
1,60
Имеем:
0,64;
0,80;
;
0,47;
0,55.
Тогда
y = 0,98 +
(x
–1,42), следовательно, y
= 0,59 x + 0,14.
;
x = 1,42 + +
(
y – 0,98) , следовательно,
x = 1,70 y
–0,25.
В следующих задачах найти коэффициент корреляции и уравнение прямой регрессии на по данным таблицы.
306. |
ξ |
– 1 |
– 0,9 |
0,2 |
0,6 |
0,9 |
1,3 |
1,7 |
1,9 |
|
2,9 |
3,3 |
5,3 |
6,1 |
6,9 |
7,5 |
8,5 |
8,7 |
|
ξ |
2,1 |
2,3 |
2,6 |
2,9 |
3,2 |
3,6 |
3,9 |
4,1 |
|
|
9,3 |
9,7 |
10,1 |
10,9 |
11,3 |
12,3 |
12,9 |
13,1 |
307. |
ξ |
1,2 |
1,9 |
2,2 |
2,6 |
2,9 |
3,3 |
3,7 |
3,9 |
|
– 0,3 |
1,8 |
2,7 |
3,8 |
4,6 |
5,5 |
7,0 |
7,8 |
|
ξ |
4,1 |
4,3 |
4,6 |
4,9 |
5,2 |
5,6 |
5,9 |
6,1 |
|
|
8,3 |
8,8 |
9,9 |
10,8 |
11,5 |
12,9 |
13,6 |
14,2 |
308. |
ξ |
– 1,1 |
– 0,9 |
– 0,2 |
0,6 |
1,6 |
2,3 |
3,2 |
3,9 |
|
– 4,2 |
– 3,8 |
– 3,3 |
– 2,3 |
– 1,5 |
– 0,6 |
0,1 |
1,0 |
|
ξ |
4,3 |
4,7 |
5,6 |
5,9 |
6,2 |
6,6 |
7,9 |
8,1 |
|
|
1,3 |
1,6 |
2,7 |
2,8 |
3,2 |
3,7 |
4,8 |
5,2 |
309. |
ξ |
– 1,1 |
– 0,4 |
0,2 |
0,6 |
1,5 |
2,4 |
3,2 |
3,7 |
|
– 3,2 |
– 1,8 |
– 0,7 |
– 0,3 |
1,9 |
3,9 |
5,4 |
6,3 |
|
ξ |
4,1 |
4,6 |
4,9 |
5,3 |
5,6 |
5,9 |
6,9 |
7,1 |
|
|
7,3 |
8,1 |
8,7 |
9,7 |
10,2 |
10,7 |
12,8 |
13,1 |
310. |
ξ |
– 1,1 |
– 0,7 |
– 0,5 |
0,3 |
0,6 |
1,3 |
1,5 |
1,9 |
|
0,7 |
1,7 |
2,0 |
3,5 |
4,2 |
5,5 |
6,1 |
6,7 |
|
ξ |
2,3 |
2,7 |
3,2 |
3,6 |
3,8 |
4,2 |
4,5 |
4,8 |
|
|
7,2 |
8,5 |
9,4 |
10,1 |
10,6 |
11,1 |
12,1 |
12,6 |
311. |
ξ |
– 1,0 |
– 0,6 |
– 0,2 |
0,5 |
1,3 |
1,6 |
2,2 |
2,5 |
|
– 7,3 |
– 5,5 |
– 3,8 |
– 1,1 |
2,2 |
3,3 |
5,2 |
7,1 |
|
ξ |
3,1 |
3,3 |
3,6 |
3,9 |
4,2 |
4,6 |
4,9 |
5,1 |
|
|
9,3 |
10,1 |
11,4 |
12,7 |
13,9 |
15,5 |
16,5 |
17,4 |
312. |
ξ |
0,1 |
0,6 |
0,9 |
1,1 |
1,4 |
1,8 |
2,2 |
2,5 |
|
– 0,7 |
0,3 |
0,8 |
1,3 |
1,7 |
2,7 |
3,4 |
4,1 |
|
ξ |
2,9 |
3,7 |
4,3 |
4,7 |
5,2 |
5,6 |
5,9 |
6,1 |
|
|
4,7 |
6,6 |
7,7 |
8,4 |
9,3 |
10,3 |
10,7 |
11,2 |
313. |
ξ |
0,2 |
0,9 |
1,2 |
1,6 |
1,9 |
2,1 |
2,5 |
2,9 |
|
– 4,3 |
– 2,4 |
– 1,4 |
– 0,2 |
0,6 |
1,4 |
2,5 |
3,6 |
|
ξ |
3,3 |
3,7 |
4,1 |
4,6 |
5,2 |
5,6 |
6,0 |
6,3 |
|
|
5,0 |
6,2 |
7,3 |
8,7 |
10,5 |
11,9 |
12,9 |
13,8 |
314. |
ξ |
– 8,1 |
– 7,9 |
– 7,2 |
– 6,6 |
– 5,6 |
– 4,3 |
– 3,2 |
– 2,9 |
|
– 1,2 |
– 0,8 |
– 0,2 |
0,3 |
1,5 |
2,6 |
3,7 |
4,1 |
|
ξ |
– 1,3 |
– 0,7 |
0,6 |
0,9 |
1,2 |
1,6 |
2,9 |
3,1 |
|
|
5,6 |
6,4 |
7,5 |
7,8 |
8,2 |
8,7 |
9,8 |
10,0 |
315. |
ξ |
– 1,1 |
– 0,8 |
– 0,3 |
0,6 |
1,6 |
1,9 |
2,2 |
2,9 |
|
4,2 |
3,8 |
3,4 |
– 2,3 |
2,5 |
1,0 |
0,9 |
0,1 |
|
ξ |
3,3 |
3,7 |
4,6 |
5,9 |
6,2 |
6,7 |
7,6 |
8,0 |
|
|
– 0,2 |
– 0,6 |
– 1,7 |
– 2,8 |
– 3,3 |
– 3,8 |
– 4,5 |
– 5,1 |
316. |
ξ |
– 1,5 |
– 1,2 |
– 0,8 |
– 0,3 |
0,6 |
0,9 |
1,2 |
1,4 |
|
6,1 |
5,4 |
4,5 |
3,5 |
1,8 |
1,3 |
0,6 |
0,3 |
|
ξ |
1,8 |
2,1 |
2,6 |
2,9 |
3,2 |
3,6 |
3,9 |
4,1 |
|
|
– 0,5 |
– 1,3 |
– 2,2 |
– 2,7 |
– 3,4 |
– 4,1 |
– 4,9 |
– 5,2 |
317. |
ξ |
– 0,1 |
0,1 |
0,3 |
0,6 |
0,9 |
1,3 |
1,8 |
2,1 |
|
– 8,4 |
– 7,6 |
– 6,4 |
– 5,0 |
– 3,4 |
– 1,6 |
1,1 |
2,4 |
|
ξ |
2,3 |
2,7 |
2,9 |
3,1 |
3,2 |
3,6 |
3,9 |
4,0 |
|
|
3,6 |
5,5 |
6,6 |
7,4 |
7,9 |
10,1 |
11,5 |
11,9 |
318. |
ξ |
– 0,8 |
– 0,5 |
– 0,2 |
0,2 |
0,6 |
1,3 |
1,7 |
1,9 |
|
– 5,3 |
– 4,6 |
– 3,6 |
– 2,3 |
– 1,3 |
0,8 |
2,2 |
2,7 |
|
ξ |
2,3 |
2,7 |
3,1 |
3,5 |
3,8 |
4,2 |
4,8 |
5,1 |
|
|
3,8 |
5,2 |
6,4 |
7,4 |
8,5 |
9,6 |
11,3 |
12,3 |
319. |
ξ |
– 1,2 |
– 0,8 |
– 0,2 |
0,4 |
1,1 |
1,3 |
1,9 |
2,3 |
|
– 10,7 |
– 9,3 |
– 8,6 |
– 4,7 |
– 1,5 |
– 0,7 |
1,7 |
3,3 |
|
ξ |
2,7 |
3,1 |
3,6 |
3,9 |
4,2 |
4,6 |
4,9 |
6,1 |
|
|
4,8 |
6,3 |
8,5 |
9,6 |
10,7 |
12,5 |
13,5 |
18,2 |
320. |
ξ |
– 2,1 |
– 1,8 |
– 1,2 |
– 0,6 |
0,6 |
0,9 |
1,2 |
1,5 |
|
7,2 |
6,7 |
5,1 |
5,6 |
4,3 |
4,2 |
3,7 |
3,5 |
|
ξ |
2,3 |
2,7 |
3,1 |
3,5 |
3,7 |
4,1 |
4,5 |
4,8 |
|
|
2,6 |
2,2 |
1,9 |
1,6 |
1,2 |
1,0 |
0,4 |
0,3 |
321. |
ξ |
– 0,1 |
0,1 |
0,3 |
0,6 |
0,9 |
1,1 |
1,2 |
1,5 |
|
– 2,7 |
1,3 |
– 0,2 |
1,7 |
1,5 |
4,5 |
5,1 |
7,0 |
|
ξ |
1,9 |
2,1 |
2,6 |
2,9 |
3,2 |
3,6 |
3,9 |
4,1 |
|
|
9,3 |
10,7 |
13,7 |
15,3 |
17,2 |
19,7 |
21,3 |
22,7 |
322. |
ξ |
– 4,3 |
– 3,9 |
– 3,2 |
– 2,9 |
– 2,6 |
– 2,3 |
– 2,1 |
– 1,9 |
|
– 10,3 |
– 8,5 |
– 5,8 |
– 4,5 |
– 3,3 |
– 2,3 |
– 1,4 |
– 0,5 |
|
ξ |
– 1,6 |
– 1,1 |
– 0,6 |
– 0,3 |
0,2 |
0,6 |
0,9 |
1,1 |
|
|
0,7 |
2,6 |
4,5 |
5,7 |
7,9 |
9,3 |
10,6 |
11,3 |
323. |
ξ |
– 3,2 |
– 2,9 |
– 2,2 |
– 1,6 |
– 1,2 |
– 0,8 |
– 0,5 |
0,1 |
|
10,3 |
9,9 |
8,4 |
7,1 |
6,5 |
5,7 |
5,1 |
3,8 |
|
ξ |
0,3 |
0,7 |
0,9 |
1,1 |
1,4 |
1,6 |
1,9 |
2,1 |
|
|
3,3 |
2,7 |
2,1 |
1,8 |
1,3 |
0,7 |
0,3 |
– 0,2 |
324. |
ξ |
– 4,1 |
– 3,9 |
– 3,2 |
– 2,8 |
– 2,3 |
– 1,9 |
– 1,5 |
– 1,2 |
|
18,3 |
17,8 |
15,6 |
14,3 |
13,0 |
11,7 |
10,4 |
9,7 |
|
ξ |
– 0,8 |
– 0,3 |
0,2 |
0,5 |
0,9 |
1,3 |
1,5 |
1,9 |
|
|
8,4 |
6,8 |
5,5 |
4,4 |
3,3 |
2,0 |
1,6 |
0,2 |
325. |
ξ |
– 0,8 |
– 0,5 |
– 0,2 |
0,7 |
1,1 |
1,3 |
1,8 |
2,0 |
|
– 4,5 |
– 3,9 |
– 3,2 |
– 1,5 |
– 0,7 |
– 0,5 |
0,6 |
1,1 |
|
ξ |
2,3 |
2,7 |
3,2 |
3,9 |
4,2 |
4,6 |
4,9 |
5,1 |
|
|
1,5 |
2,6 |
3,4 |
4,7 |
5,5 |
6,1 |
6,8 |
7,3 |
326. |
ξ |
– 0,4 |
– 0,1 |
0,2 |
0,4 |
0,6 |
0,8 |
1,1 |
1,2 |
|
– 5,1 |
– 3,6 |
– 1,9 |
– 1,0 |
0,1 |
0,9 |
2,6 |
2,9 |
|
ξ |
1,3 |
1,5 |
1,7 |
1,8 |
2,1 |
2,4 |
2,5 |
2,7 |
|
|
3,5 |
4,6 |
5,4 |
6,1 |
7,5 |
8,9 |
9,6 |
10,5 |
327. |
ξ |
– 2,3 |
– 2,1 |
– 1,9 |
– 1,6 |
– 1,3 |
– 0,9 |
– 0,5 |
– 0,2 |
|
– 0,5 |
– 0,3 |
0,2 |
0,9 |
1,5 |
2,2 |
2,9 |
3,7 |
|
ξ |
0,3 |
0,7 |
0,9 |
1,2 |
1,5 |
1,8 |
2,1 |
2,7 |
|
|
4,5 |
5,5 |
5,7 |
6,4 |
7,1 |
7,7 |
8,3 |
9,4 |
328. |
ξ |
– 1,2 |
– 0,8 |
– 0,2 |
0,6 |
1,2 |
2,2 |
2,6 |
3,2 |
|
– 3,5 |
– 3,5 |
– 3,0 |
– 2,8 |
– 2,4 |
– 1,8 |
– 1,6 |
– 1,3 |
|
ξ |
3,8 |
4,4 |
5,2 |
5,8 |
6,2 |
6,6 |
7,8 |
8,8 |
|
|
– 1,2 |
– 0,7 |
– 0,3 |
0,0 |
0,2 |
0,3 |
0,8 |
1,5 |
329. |
ξ |
– 4,8 |
– 4,4 |
– 3,6 |
– 3,2 |
– 2,4 |
– 1,2 |
– 0,8 |
– 0,2 |
|
7,5 |
7,1 |
6,9 |
6,6 |
6,1 |
5,6 |
5,3 |
5,0 |
|
ξ |
0,2 |
0,8 |
1,6 |
2,2 |
3,2 |
3,6 |
4,8 |
5,6 |
|
|
4,8 |
4,6 |
4,3 |
3,8 |
3,5 |
3,1 |
2,5 |
2,2 |
330. |
ξ |
– 1,0 |
– 0,8 |
– 0,2 |
0,6 |
1,0 |
2,3 |
3,2 |
3,9 |
|
– 3,3 |
– 3,4 |
– 3,0 |
– 2,8 |
– 2,5 |
– 2,1 |
– 1,7 |
– 1,5 |
|
ξ |
4,3 |
5,7 |
6,6 |
7,9 |
8,2 |
9,6 |
9,9 |
11,5 |
|
|
– 1,2 |
– 0,8 |
– 0,3 |
0,1 |
0,3 |
0,8 |
1,0 |
1,6 |
331. |
ξ |
– 0,7 |
– 0,3 |
0,5 |
1,3 |
1,6 |
2,1 |
2,4 |
2,9 |
|
– 5,6 |
– 4,4 |
– 1,1 |
2,4 |
3,5 |
5,3 |
6,6 |
8,7 |
|
ξ |
3,5 |
3,8 |
4,2 |
4,6 |
5,6 |
6,1 |
6,8 |
8,2 |
|
|
10,8 |
12,1 |
13,9 |
15,2 |
19,5 |
21,2 |
24,9 |
29,4 |
332. |
ξ |
– 2,4 |
– 2,2 |
– 1,6 |
– 0,6 |
– 0,4 |
0,1 |
0,5 |
0,8 |
|
7,9 |
7,1 |
6,4 |
5,2 |
3,9 |
2,9 |
2,2 |
1,5 |
|
ξ |
1,2 |
1,6 |
1,9 |
2,3 |
2,7 |
3,2 |
3,5 |
4,1 |
|
|
0,6 |
– 0,3 |
– 0,7 |
– 1,8 |
– 2,2 |
– 3,5 |
– 4,2 |
– 5,4 |
333. |
ξ |
– 2,2 |
– 1,8 |
– 1,3 |
– 0,7 |
– 0,3 |
0,1 |
0,5 |
0,9 |
|
– 11,5 |
– 10,5 |
– 8,8 |
– 4,6 |
– 4,9 |
– 4,6 |
– 3,6 |
– 2,4 |
|
ξ |
1,3 |
1,6 |
2,1 |
2,5 |
2,8 |
3,2 |
3,6 |
4,2 |
|
|
– 1,1 |
– 0,1 |
1,2 |
2,5 |
3,5 |
4,5 |
5,9 |
7,6 |
334. |
ξ |
– 7,1 |
– 6,6 |
– 5,3 |
– 4,4 |
– 4,1 |
– 3,3 |
– 2,7 |
– 1,9 |
|
– 2,1 |
– 1,6 |
– 0,3 |
0,6 |
0,8 |
1,8 |
2,2 |
3,1 |
|
ξ |
– 0,8 |
– 0,2 |
0,2 |
0,9 |
1,2 |
2,6 |
2,9 |
4,1 |
|
|
4,3 |
4,7 |
5,2 |
6,0 |
6,1 |
7,7 |
7,8 |
9,2 |
335. |
ξ |
– 2,2 |
– 1,8 |
– 1,3 |
– 0,7 |
– 0,3 |
0,1 |
0,5 |
0,9 |
|
9,9 |
8,1 |
5,4 |
2,5 |
0,4 |
– 1,4 |
– 3,6 |
– 5,4 |
|
ξ |
1,3 |
1,6 |
1,8 |
2,1 |
2,5 |
2,8 |
3,2 |
3,6 |
|
|
– 7,6 |
– 9,1 |
– 9,9 |
– 11,4 |
– 13,6 |
– 14,9 |
– 17,0 |
– 18,9 |
Если линия регрессии не является прямой линией, то регрессию называют криволинейной. Криволинейную регрессию называют параболической (полиномиальной), если ее уравнение имеет вид: y a0xn + a1xn–1 + ... + an.
В частности, выборочное уравнение параболической регрессии 2-го порядка отыскивается в виде y
=
,
где коэффициенты a,
b и c
определяются из системы уравнений:
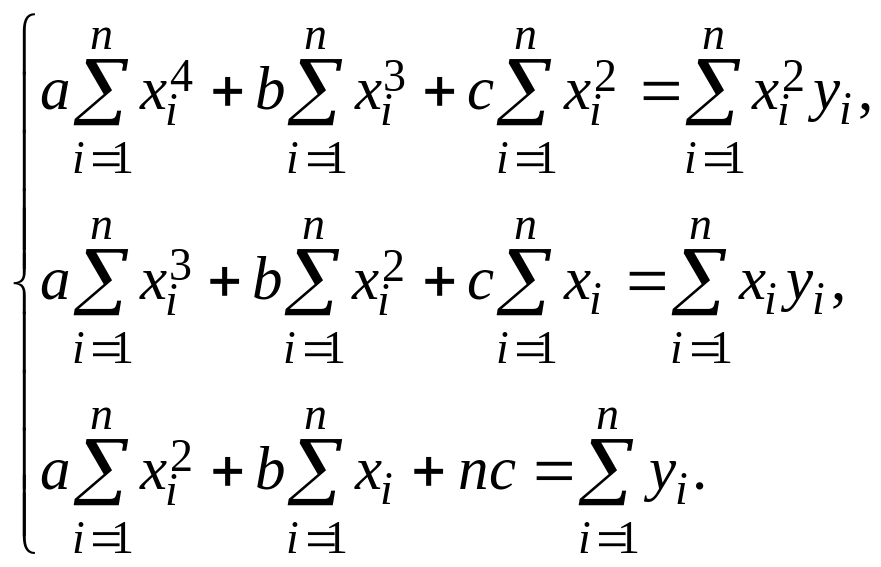
В следующих задачах найти выборочное уравнение параболической регрессии 2-го порядка регрессии на по данным таблицы.
336. |
ξ |
1 |
3 |
4 |
6 |
7 |
|
1,2 |
6,9 |
24,8 |
121,1 |
210,7 |
|
ξ |
8 |
10 |
12 |
14 |
15 |
|
|
337,2 |
720,9 |
1321,2 |
2185,0 |
2731,3 |
337. |
ξ |
2 |
4 |
5 |
7 |
8 |
|
8,1 |
62,2 |
121,9 |
337,7 |
506,2 |
|
ξ |
9 |
10 |
12 |
14 |
16 |
|
|
721,8 |
991,9 |
1718,2 |
2731,8 |
4082,1 |
338. |
ξ |
–1 |
1 |
3 |
4 |
5 |
|
–0,9 |
1,3 |
2,8 |
19,1 |
52,8 |
|
ξ |
7 |
9 |
10 |
12 |
13 |
|
|
199,2 |
489,1 |
702,9 |
1298,8 |
1693,2 |
339. |
ξ |
–1 |
0 |
2 |
4 |
6 |
|
–1,1 |
–0,2 |
13,8 |
84,1 |
258,2 |
|
ξ |
7 |
8 |
10 |
11 |
12 |
|
|
399,0 |
583,9 |
1109,8 |
1463,3 |
1883,9 |
340. |
ξ |
–3 |
–2 |
1 |
3 |
4 |
|
–24,8 |
–10,1 |
–0,8 |
35,2 |
79,9 |
|
ξ |
5 |
7 |
8 |
9 |
10 |
|
|
151,3 |
394,9 |
580,1 |
814,8 |
1106,2 |
341. |
ξ |
–4 |
–3 |
–1 |
0 |
2 |
|
–73,9 |
–31,2 |
–0,8 |
2,1 |
3,7 |
|
ξ |
3 |
5 |
6 |
7 |
8 |
|
|
16,9 |
97,2 |
176,1 |
288,8 |
442,1 |
342. |
ξ |
–5 |
–3 |
–2 |
–1 |
1 |
|
–134,1 |
–31,9 |
–11,0 |
–2,2 |
3,8 |
|
ξ |
3 |
4 |
6 |
7 |
9 |
|
|
34,1 |
73,3 |
228,9 |
358,2 |
747,8 |
343. |
ξ |
1 |
2 |
3 |
4 |
5 |
|
3,2 |
9,9 |
27,1 |
59,8 |
115,2 |
|
ξ |
6 |
7 |
8 |
9 |
10 |
|
|
197,9 |
314,7 |
472,2 |
675,3 |
929,8 |
344. |
ξ |
–2 |
–1 |
0 |
1 |
2 |
|
1,9 |
5,1 |
2,2 |
–0,8 |
1,8 |
|
ξ |
4 |
5 |
7 |
8 |
9 |
|
|
50,1 |
106,7 |
317,2 |
482,1 |
694,9 |
345. |
ξ |
–3 |
–2 |
–1 |
1 |
3 |
|
-28,2 |
–8,8 |
–2,3 |
0,1 |
25,9 |
|
ξ |
4 |
6 |
7 |
8 |
10 |
|
|
63,2 |
214,7 |
341,9 |
511,1 |
999,2 |
346. |
ξ |
–4 |
–3 |
–2 |
–1 |
0 |
|
–119,2 |
–58,9 |
–23,1 |
–5,0 |
0,8 |
|
ξ |
1 |
2 |
3 |
4 |
5 |
|
|
1,1 |
0,7 |
7,2 |
24,8 |
61,3 |
347. |
ξ |
–2 |
–1 |
1 |
2 |
3 |
|
–4,2 |
1,9 |
2,2 |
7,7 |
26,1 |
|
ξ |
5 |
6 |
7 |
8 |
10 |
|
|
121,8 |
212,2 |
338,1 |
505,8 |
992,2 |
348. |
ξ |
–5 |
–4 |
–3 |
1 |
2 |
|
–197,2 |
–108,9 |
–51,2 |
0,8 |
–0,9 |
|
ξ |
3 |
4 |
5 |
6 |
7 |
|
|
3,3 |
19,1 |
52,8 |
111,1 |
199,2 |
349. |
ξ |
–1 |
0 |
2 |
3 |
4 |
|
–0,8 |
0,2 |
13,7 |
39,1 |
84,2 |
|
ξ |
6 |
7 |
8 |
9 |
10 |
|
|
257,9 |
399,3 |
584,2 |
818,8 |
1109,9 |
350. |
ξ |
–3 |
–1 |
0 |
1 |
3 |
|
–25,1 |
–4,9 |
–4,2 |
–0,8 |
34,9 |
|
ξ |
5 |
7 |
8 |
10 |
11 |
|
|
151,0 |
396,1 |
579,9 |
1106,2 |
1458,7 |
351. |
ξ |
–6 |
–4 |
–2 |
0 |
2 |
|
–244,2 |
–73,8 |
–8,1 |
1,7 |
3,9 |
|
ξ |
4 |
6 |
8 |
10 |
12 |
|
|
46,2 |
175,8 |
442,3 |
892,1 |
1573,8 |
352. |
ξ |
–5 |
–4 |
–2 |
–1 |
0 |
|
–134,2 |
–70,9 |
–8,8 |
–2,2 |
0,7 |
|
ξ |
1 |
2 |
3 |
5 |
7 |
|
|
3,9 |
12,8 |
34,2 |
135,9 |
358,1 |
353. |
ξ |
–1 |
0 |
1 |
2 |
3 |
|
–5,1 |
0,2 |
2,8 |
9,9 |
27,1 |
|
ξ |
4 |
5 |
6 |
7 |
8 |
|
|
49,7 |
114,9 |
198,2 |
315,1 |
471,8 |
354. |
ξ |
–4 |
–3 |
–2 |
–1 |
0 |
|
–46,2 |
–12,9 |
2,2 |
4,8 |
2,1 |
|
ξ |
1 |
2 |
3 |
4 |
5 |
|
|
–0,9 |
1,8 |
17,3 |
49,9 |
107,2 |
355. |
ξ |
–2 |
–1 |
0 |
1 |
2 |
|
–9,1 |
–1,9 |
–1,2 |
0,1 |
6,8 |
|
ξ |
3 |
4 |
5 |
6 |
7 |
|
|
27,3 |
63,2 |
123,8 |
215,1 |
341,9 |
356. |
ξ |
– 5 |
– 3,2 |
– 0,1 |
0,1 |
0,3 |
|
45,10 |
24,83 |
5,30 |
4,72 |
4,18 |
|
ξ |
0,9 |
1,2 |
1,5 |
2,4 |
3,2 |
|
|
3,11 |
2,83 |
2,76 |
3,56 |
5,63 |
357. |
ξ |
– 5,1 |
– 3,8 |
– 0,2 |
0,4 |
0,7 |
|
14,80 |
5,9 |
– 1,36 |
– 0,03 |
0,28 |
|
ξ |
1,1 |
1,6 |
1,8 |
2,4 |
3,3 |
|
|
2,42 |
4,75 |
5,85 |
9,56 |
16,48 |
358. |
ξ |
– 8,2 |
– 7,4 |
– 6,3 |
– 5,5 |
– 4,7 |
|
53,8 |
43,0 |
30,1 |
22,2 |
15,7 |
|
ξ |
– 3,1 |
– 2,4 |
– 1,5 |
– 0,4 |
0,8 |
|
|
6,4 |
4,0 |
2,3 |
2,3 |
5,2 |
359. |
ξ |
– 4,1 |
– 3,2 |
– 0,1 |
1,3 |
2,4 |
|
35,22 |
25,03 |
2,41 |
– 1,52 |
– 1,84 |
|
ξ |
3,1 |
3,5 |
4,3 |
5,1 |
5,5 |
|
|
– 0,78 |
0,24 |
3,28 |
7,62 |
10,24 |
В следующих задачах составить корреляционную таблицу. Найти выборочную функцию регрессии по , выборочную функцию регрессии по и коэффициент корреляции.
360. Пусть 1/2, где 1 – предел текучести стали, 2 – предел прочности стали, а – процентное содержание углерода в стали. В результате 79 опытов получена следующая корреляционная таблица значений и .
x y |
0,5 |
0,6 |
0,7 |
0,8 |
|
0,5 |
0 |
2 |
0 |
8 |
10 |
0,6 |
0 |
4 |
2 |
9 |
15 |
0,7 |
2 |
12 |
3 |
1 |
18 |
0,8 |
21 |
14 |
0 |
0 |
35 |
0,9 |
1 |
0 |
0 |
0 |
1 |
|
24 |
32 |
5 |
18 |
79 |
Требуется найти выборочный коэффициент корреляции и выборочные уравнения прямых регрессии. Имеем:
;
0,105;
;
0,110;
.
Найдем выборочные уравнения прямых регрессии:
y
–0,931x + 1,277;
x
–0,849y + 1,231.
352. |
30; 26 |
40; 56 |
25; 26 |
30; 36 |
35; 36 |
40; 46 |
30; 36 |
35; 46 |
25; 16 |
30; 36 |
30; 36 |
35; 46 |
30;3 6 |
35; 46 |
30; 36 |
25; 26 |
30; 46 |
40; 46 |
30; 36 |
35; 56 |
20; 16 |
30; 26 |
30; 36 |
35; 46 |
30; 46 |
40; 3 6 |
25; 26 |
30; 36 |
40; 36 |
35; 46 |
30; 46 |
30; 36 |
30; 26 |
40; 46 |
30; 36 |
30; 36 |
30; 36 |
30; 26 |
35; 36 |
40; 36 |
25; 26 |
30 ;36 |
40; 36 |
40; 36 |
40; 56 |
30; 36 |
35; 46 |
30; 26 |
35; 46 |
25; 16 |
30; 36 |
40; 46 |
30; 36 |
30; 36 |
25; 16 |
25; 16 |
30; 36 |
25; 26 |
35; 46 |
40; 56 |
30; 36 |
30; 46 |
30; 36 |
40; 36 |
30; 26 |
30; 36 |
35; 36 |
35; 46 |
40; 46 |
25; 16 |
30; 36 |
25; 26 |
30; 36 |
30; 46 |
20; 16 |
35; 46 |
30; 36 |
40; 36 |
35; 46 |
30; 36 |
30; 26 |
35; 46 |
40; 46 |
25; 16 |
30; 36 |
35; 46 |
30; 36 |
40; 36 |
30; 26 |
40; 56 |
25; 16 |
30; 36 |
35; 46 |
30; 36 |
40; 36 |
30; 36 |
40; 46 |
20; 16 |
40; 36 |
25; 16 |
|
|
|
353. |
15; 120 |
10;140 |
20; 160 |
5; 160 |
5; 120 |
25; 140 |
10; 120 |
40; 160 |
20; 140 |
20; 160 |
35; 160 |
15; 140 |
20; 140 |
10; 120 |
20; 140 |
20; 140 |
35; 180 |
15; 140 |
5; 100 |
20; 140 |
35; 160 |
40; 160 |
25; 140 |
35; 180 |
5; 120 |
20; 140 |
10; 120 |
25; 140 |
15; 140 |
25; 140 |
20; 140 |
35; 180 |
5; 120 |
15; 120 |
25; 140 |
20; 140 |
10; 120 |
20; 140 |
25; 140 |
10; 100 |
20; 140 |
25; 140 |
5; 120 |
15; 120 |
15; 120 |
20; 140 |
5; 120 |
15; 140 |
25; 140 |
40; 180 |
35; 180 |
20; 140 |
20; 140 |
10; 100 |
25; 140 |
15; 140 |
20; 140 |
15; 140 |
10; 120 |
20; 140 |
15; 140 |
25; 140 |
20; 140 |
10; 120 |
20; 140 |
5; 100 |
20; 140 |
35; 180 |
25; 140 |
20; 140 |
20; 140 |
15; 120 |
20; 140 |
5; 120 |
25; 140 |
10; 120 |
25; 140 |
20; 140 |
15; 120 |
15; 140 |
20; 140 |
35; 180 |
20; 140 |
40; 180 |
20; 140 |
25; 140 |
15; 120 |
25; 140 |
20; 140 |
15; 140 |
5; 100 |
35; 180 |
10; 120 |
25; 140 |
5; 100 |
20; 140 |
20; 140 |
15; 140 |
20; 140 |
35; 180 |
|
|
|
|
|
|
|
354. |
30; 120 |
10; 160 |
30; 100 |
10; 160 |
20; 140 |
5; 160 |
20; 140 |
30; 100 |
30; 100 |
10; 160 |
20; 140 |
10; 160 |
35; 120 |
10; 160 |
30; 120 |
10; 160 |
25; 140 |
15; 140 |
35; 120 |
15; 160 |
5; 160 |
25; 140 |
20; 140 |
15; 140 |
20; 140 |
35; 100 |
10; 160 |
15; 140 |
10; 160 |
30; 120 |
15; 140 |
30; 100 |
15; 160 |
25; 140 |
15; 140 |
30; 120 |
5; 160 |
20; 140 |
15; 160 |
20; 140 |
25; 140 |
15; 140 |
20; 140 |
5; 180 |
15; 140 |
20; 140 |
10; 180 |
30; 100 |
15; 140 |
20; 140 |
30; 100 |
5; 180 |
30; 100 |
20; 140 |
20; 180 |
35; 100 |
15; 140 |
30; 120 |
5; 160 |
25; 140 |
20; 140 |
25; 140 |
5; 180 |
20; 140 |
15; 140 |
20; 140 |
15; 160 |
30; 100 |
20; 140 |
15; 140 |
20; 140 |
30; 120 |
15; 140 |
20; 140 |
25; 140 |
15; 140 |
25; 140 |
5; 180 |
20; 140 |
15; 140 |
10; 180 |
30; 100 |
5;1 60 |
30; 100 |
5; 160 |
20; 140 |
30; 100 |
25; 140 |
30; 100 |
20; 140 |
15; 140 |
20; 140 |
15; 160 |
30; 120 |
25; 140 |
15; 140 |
20; 140 |
5; 160 |
20; 180 |
30; 120 |
|
|
|
|
|
|
|
355. |
29; 50 |
41; 70 |
35; 55 |
41; 60 |
38; 60 |
35; 50 |
41; 70 |
32; 50 |
44; 70 |
32; 55 |
47; 70 |
38; 55 |
38; 65 |
35; 60 |
41; 65 |
38; 60 |
47; 75 |
35; 55 |
44; 65 |
38; 65 |
35; 55 |
44; 70 |
38; 60 |
44; 70 |
38; 60 |
38; 65 |
41; 60 |
41; 60 |
38; 65 |
38; 55 |
41; 65 |
38; 65 |
32; 50 |
41; 60 |
38; 65 |
41; 65 |
38; 65 |
41; 70 |
35; 60 |
29; 50 |
47; 75 |
38; 60 |
41; 70 |
44; 65 |
35; 60 |
38; 65 |
38; 60 |
41; 65 |
35; 50 |
41; 70 |
41; 60 |
35; 55 |
38; 60 |
41; 60 |
38; 65 |
41; 60 |
38; 65 |
41; 70 |
38; 65 |
35; 55 |
38; 65 |
41; 65 |
47; 70 |
32; 50 |
44; 65 |
38; 60 |
44; 70 |
44; 75 |
44; 70 |
38; 65 |
41; 65 |
38; 65 |
38; 55 |
38; 65 |
38; 60 |
41; 70 |
35; 60 |
38; 60 |
38; 65 |
41; 65 |
35; 55 |
41; 60 |
47; 75 |
41; 65 |
35; 55 |
38; 65 |
38; 65 |
38; 65 |
41; 70 |
38; 65 |
41; 70 |
38; 65 |
32; 50 |
44; 70 |
38; 65 |
41; 65 |
35; 55 |
41; 65 |
35; 60 |
38; 55 |
|
|
|
|
|
|
|
|
|
356. |
28; 150 |
33; 175 |
28; 150 |
33; 175 |
28; 150 |
38; 225 |
23; 175 |
23; 125 |
33; 175 |
28; 175 |
38; 200 |
33; 175 |
38; 200 |
23; 150 |
33; 175 |
38; 200 |
48; 250 |
23; 175 |
33; 175 |
43; 225 |
28; 150 |
33; 175 |
38; 225 |
33; 200 |
33; 175 |
28; 150 |
33; 175 |
33; 200 |
18; 150 |
33; 175 |
28; 175 |
38; 200 |
48; 250 |
38; 200 |
43; 250 |
23; 175 |
38; 200 |
33; 175 |
28; 175 |
33; 175 |
23; 125 |
43; 225 |
33; 200 |
38; 200 |
28; 200 |
33; 175 |
28; 150 |
33; 175 |
28; 200 |
33; 175 |
33; 200 |
33; 175 |
23; 175 |
18; 150 |
38; 200 |
33; 175 |
23; 150 |
43; 250 |
33; 200 |
33; 175 |
38; 225 |
33; 175 |
33; 175 |
28; 150 |
33; 200 |
33; 175 |
33; 200 |
33; 175 |
43; 225 |
38; 200 |
38; 225 |
28; 150 |
33; 175 |
38; 200 |
23; 175 |
33; 175 |
33; 200 |
33; 175 |
43; 225 |
33; 175 |
33; 175 |
23; 175 |
33; 175 |
28; 175 |
23; 225 |
38; 225 |
43; 225 |
38; 225 |
38; 200 |
28; 150 |
33; 175 |
23; 150 |
33; 175 |
33; 200 |
33; 175 |
38; 200 |
33; 175 |
33; 175 |
33; 175 |
33; 200 |
|
|
|
|
|
|
|
357. |
20; 24 |
27; 27 |
13; 15 |
27; 24 |
13; 21 |
27; 27 |
20; 18 |
13; 21 |
13; 18 |
27; 21 |
34; 24 |
20; 18 |
34; 24 |
27; 24 |
34; 24 |
27; 24 |
34; 27 |
27 ;24 |
20; 21 |
27; 24 |
13; 15 |
27; 27 |
34; 27 |
20; 21 |
20; 24 |
20; 21 |
27; 24 |
20; 18 |
20; 24 |
20; 21 |
34; 27 |
20; 24 |
27; 24 |
34; 27 |
27; 24 |
34; 30 |
34; 24 |
27; 24 |
13; 18 |
34; 27 |
20; 18 |
34; 30 |
20; 21 |
27; 27 |
13; 18 |
27; 24 |
13; 21 |
27; 24 |
20; 24 |
27; 24 |
27; 24 |
20; 24 |
27; 24 |
6; 12 |
34; 27 |
20; 24 |
27; 27 |
6; 15 |
34; 27 |
13; 21 |
27; 27 |
20; 24 |
34; 24 |
27 ;27 |
20; 24 |
41; 30 |
20; 24 |
27; 24 |
27; 27 |
34; 24 |
20; 21 |
41; 30 |
27; 24 |
20; 24 |
41; 33 |
20; 21 |
27; 24 |
27; 21 |
34; 24 |
27; 24 |
34; 27 |
13; 21 |
34; 24 |
34; 30 |
27; 24 |
34; 27 |
34; 24 |
20; 24 |
34; 24 |
20; 18 |
20; 24 |
34; 24 |
27; 24 |
20; 18 |
34; 27 |
27; 24 |
20; 21 |
27; 24 |
20; 24 |
27; 27 |
|
|
|
|
|
|
|
|
|
358. |
40; 60 |
48; 40 |
24; 70 |
48; 40 |
49; 60 |
48; 60 |
40; 60 |
48; 60 |
40; 60 |
40; 60 |
48; 50 |
40; 60 |
32; 60 |
40; 60 |
32; 60 |
40; 60 |
32; 60 |
32; 70 |
48; 60 |
48; 60 |
40; 60 |
24; 70 |
40; 60 |
24; 70 |
64; 30 |
48; 50 |
40; 60 |
40; 60 |
32; 70 |
40; 60 |
48; 50 |
56; 30 |
24; 70 |
40; 50 |
40; 60 |
48; 60 |
32; 70 |
56; 30 |
24; 80 |
56; 30 |
32; 70 |
32; 60 |
40; 60 |
32; 60 |
48; 60 |
32; 60 |
48; 60 |
48; 50 |
40; 60 |
24; 70 |
32; 70 |
64; 30 |
48; 60 |
40; 60 |
24; 70 |
16; 90 |
40; 60 |
32; 80 |
32; 60 |
48; 60 |
32; 60 |
40; 60 |
32; 60 |
32; 80 |
32; 60 |
40; 60 |
48; 50 |
16; 80 |
24; 90 |
32; 60 |
40; 60 |
48; 40 |
40; 60 |
56; 40 |
40; 60 |
24; 80 |
40; 60 |
40; 50 |
32; 70 |
40; 60 |
48; 50 |
40; 60 |
32; 60 |
48; 40 |
32; 60 |
40; 60 |
32; 60 |
40; 60 |
40; 60 |
48; 40 |
40; 60 |
32; 70 |
56; 40 |
24; 70 |
48; 50 |
32; 70 |
40; 60 |
32; 70 |
56; 40 |
40; 60 |
|
|
|
|
|
|
|
|
|
359. |
48; 20 |
27; 10 |
13; 10 |
41; 25 |
34; 15 |
41; 15 |
13; 10 |
34; 15 |
48; 20 |
41; 15 |
41; 25 |
34; 15 |
48; 20 |
34; 15 |
41; 15 |
34; 15 |
48; 20 |
41; 25 |
41; 15 |
48; 20 |
34; 15 |
20; 15 |
34; 15 |
41; 20 |
34; 15 |
20; 15 |
34; 15 |
27; 15 |
20; 15 |
34; 15 |
41; 20 |
20; 10 |
62; 35 |
34; 15 |
41; 20 |
34; 15 |
41; 15 |
48; 20 |
34; 15 |
41; 15 |
27; 10 |
48; 25 |
13; 5 |
27; 10 |
34; 15 |
41; 25 |
48; 20 |
55; 25 |
34; 15 |
55; 25 |
34; 15 |
20; 15 |
34; 15 |
48; 25 |
41; 15 |
34; 15 |
41; 15 |
13; 10 |
34; 20 |
34; 15 |
48; 20 |
34; 15 |
41; 15 |
20; 15 |
34; 15 |
27; 15 |
48; 20 |
41; 20 |
55; 30 |
48; 20 |
34; 15 |
34; 20 |
48; 20 |
13; 5 |
62; 30 |
34; 15 |
27; 15 |
20; 10 |
41; 15 |
34; 15 |
27; 15 |
41; 20 |
34; 15 |
20; 10 |
13; 5 |
27; 15 |
13; 10 |
48; 20 |
13; 5 |
41; 15 |
62; 35 |
20; 10 |
27; 15 |
41; 25 |
34; 15 |
48; 20 |
34; 15 |
20; 15 |
41; 25 |
34; 15 |
|
|
|
|
|
|
|
|
|
360. |
2; 19 |
16; 13 |
9; 19 |
37; 1 |
16; 13 |
37;7 |
9;19 |
44; 1 |
9; 19 |
23; 13 |
23; 25 |
37; 7 |
30; 13 |
23; 13 |
9; 19 |
30;13 |
23;13 |
37; 7 |
16; 13 |
16; 13 |
23; 13 |
16; 19 |
37; 1 |
16; 13 |
23; 13 |
37;1 |
16;13 |
9; 25 |
16; 13 |
23; 13 |
23; 25 |
9; 19 |
23; 13 |
30; 13 |
16; 19 |
23;13 |
44;7 |
30; 13 |
23; 13 |
2; 25 |
23; 13 |
37; 1 |
2; 19 |
37; 1 |
23; 13 |
37;1 |
16;19 |
23; 13 |
2; 25 |
23; 13 |
37; 1 |
16; 19 |
23; 13 |
44; 7 |
9; 19 |
37;7 |
37;7 |
23; 13 |
30;13 |
16; 19 |
9; 19 |
23; 13 |
16; 13 |
37; 1 |
30; 13 |
2;19 |
16;13 |
44;7 |
16;13 |
37; 1 |
23; 13 |
16; 19 |
37; 7 |
9; 19 |
23; 13 |
37;7 |
37;1 |
30; 13 |
9;19 |
9 ;25 |
16; 13 |
23; 13 |
30; 13 |
23; 13 |
16; 13 |
37;1 |
9;19 |
30; 13 |
23; 13 |
23; 13 |
37; 1 |
2; 19 |
23; 13 |
16; 13 |
37; 7 |
44;1 |
23;13 |
30; 13 |
23; 13 |
16; 13 |
|
|
|
|
|
|
|
|
|
361. |
24; 20 |
18; 11 |
16; 8 |
24; 23 |
18; 11 |
20; 14 |
20; 17 |
18; 11 |
16; 11 |
20; 14 |
14; 11 |
22; 17 |
20; 17 |
18; 11 |
16; 14 |
22; 17 |
26; 23 |
16; 8 |
24; 20 |
18; 14 |
20; 14 |
20; 17 |
20; 14 |
20; 17 |
20; 14 |
24; 20 |
18; 11 |
18; 17 |
22; 17 |
20; 14 |
20; 17 |
20; 14 |
18; 14 |
20; 14 |
20; 17 |
22; 17 |
20; 17 |
22; 17 |
24; 20 |
16; 11 |
20; 14 |
18; 11 |
16; 14 |
20; 17 |
18; 11 |
20; 14 |
22; 20 |
20; 14 |
22; 20 |
22; 17 |
18; 17 |
20; 14 |
22; 17 |
22; 20 |
20; 14 |
20; 17 |
18; 14 |
20; 17 |
18; 11 |
18; 14 |
20; 17 |
24; 20 |
20; 17 |
16; 14 |
22; 17 |
20; 14 |
22; 20 |
22; 17 |
16; 14 |
14; 11 |
26; 23 |
16; 11 |
20; 14 |
22; 17 |
20; 14 |
22; 20 |
22; 17 |
24; 23 |
22; 20 |
20; 14 |
18; 11 |
20; 14 |
20; 17 |
20; 14 |
18; 11 |
20; 17 |
16; 14 |
20; 17 |
20; 14 |
16; 11 |
20; 14 |
20; 17 |
20; 14 |
22; 17 |
24; 20 |
22; 17 |
20; 14 |
20; 14 |
16; 14 |
20; 14 |
|
|
|
|
|
|
|
|
|
362. |
43; 56 |
37; 66 |
25; 46 |
25; 36 |
31; 56 |
31; 46 |
31; 56 |
43; 66 |
43; 56 |
31; 56 |
25; 46 |
31; 56 |
31; 66 |
31; 56 |
25; 46 |
31; 56 |
31; 66 |
49; 76 |
31; 56 |
37; 76 |
31; 56 |
37; 66 |
43; 76 |
37; 66 |
31; 56 |
37; 66 |
43; 76 |
31; 46 |
49; 76 |
43; 76 |
37; 56 |
31; 56 |
31; 46 |
31; 56 |
37; 56 |
43; 66 |
37; 66 |
43; 56 |
25; 46 |
25; 36 |
31; 56 |
31; 46 |
43; 66 |
25; 36 |
31; 56 |
31; 46 |
31; 56 |
49; 76 |
43; 56 |
43; 76 |
37; 66 |
31; 56 |
31; 66 |
43; 66 |
37; 66 |
43; 76 |
43; 56 |
19; 36 |
31; 56 |
31; 66 |
25; 46 |
43; 56 |
37; 66 |
43; 56 |
25; 46 |
43; 56 |
49; 76 |
43; 56 |
31; 56 |
31; 56 |
37; 66 |
49; 76 |
31; 46 |
31; 56 |
19; 36 |
31; 56 |
37; 66 |
31; 56 |
31; 46 |
25; 36 |
31; 56 |
31; 46 |
31; 56 |
25; 36 |
31; 56 |
31; 46 |
31; 56 |
19; 36 |
25; 46 |
31; 56 |
37; 66 |
31; 56 |
37; 56 |
31; 56 |
43; 56 |
31; 56 |
43; 76 |
31; 46 |
49; 76 |
37; 66 |
|
|
|
|
|
|
|
|
|
363. |
43; 60 |
38; 68 |
53; 52 |
43; 68 |
58; 44 |
38; 68 |
48; 60 |
43; 60 |
38; 68 |
43; 60 |
43; 68 |
58; 44 |
48; 52 |
43; 60 |
43; 68 |
43; 60 |
53; 36 |
58; 36 |
43; 60 |
48; 44 |
38; 76 |
53; 36 |
48; 68 |
53; 36 |
38; 76 |
53; 36 |
33; 84 |
43; 60 |
48; 60 |
43; 60 |
48; 52 |
58; 44 |
28; 84 |
43; 60 |
53; 36 |
58; 44 |
53; 44 |
53; 44 |
43; 76 |
43; 76 |
43; 60 |
48; 60 |
43; 60 |
48; 52 |
43; 60 |
43; 60 |
48; 60 |
33; 76 |
43; 60 |
58; 44 |
33; 84 |
43; 60 |
53; 44 |
58; 36 |
43; 60 |
48; 52 |
43; 60 |
53; 60 |
38; 68 |
48; 60 |
43; 60 |
48; 60 |
53; 36 |
43; 60 |
48; 52 |
43; 60 |
48; 60 |
43; 60 |
53; 36 |
36; 68 |
48; 52 |
43; 60 |
43; 60 |
38; 68 |
43; 60 |
53; 44 |
43; 60 |
38; 76 |
48; 60 |
43; 60 |
53; 52 |
48; 68 |
48; 52 |
48; 52 |
53; 60 |
43; 60 |
48; 52 |
43; 60 |
53; 36 |
48; 52 |
38; 76 |
43; 60 |
58; 44 |
53; 44 |
43; 60 |
53; 44 |
43; 60 |
33; 76 |
43; 60 |
53; 36 |
|
|
|
|
|
|
|
|
|
364. |
35; 11 |
19; 31 |
23; 31 |
15; 41 |
23; 31 |
15; 41 |
23; 31 |
27; 31 |
23; 31 |
23; 31 |
19; 41 |
23; 31 |
19; 41 |
31; 11 |
11; 51 |
25; 21 |
19; 41 |
11; 41 |
31; 11 |
15; 41 |
31; 21 |
11; 41 |
31; 21 |
19; 31 |
23; 31 |
19; 31 |
31; 11 |
15; 41 |
27; 31 |
23; 31 |
15; 51 |
23; 31 |
19; 31 |
35; 21 |
19; 31 |
23; 31 |
19; 31 |
27; 31 |
19; 41 |
15; 41 |
35; 21 |
27; 31 |
23; 31 |
15; 41 |
23; 31 |
27; 31 |
23; 31 |
31; 21 |
19; 31 |
31; 21 |
11; 41 |
11; 41 |
27; 31 |
23; 31 |
31; 11 |
23; 31 |
15; 51 |
11; 41 |
31; 11 |
19; 41 |
23; 31 |
19; 31 |
31; 21 |
31; 11 |
23; 51 |
27; 31 |
31; 21 |
19; 31 |
35; 21 |
27; 31 |
31; 11 |
15; 41 |
27; 31 |
19; 31 |
23; 31 |
31; 11 |
11; 51 |
23; 31 |
15; 41 |
19; 31 |
23; 31 |
27; 31 |
31; 11 |
35; 11 |
19; 31 |
23; 31 |
31; 11 |
19; 31 |
31; 11 |
23; 31 |
19; 41 |
23; 31 |
31; 11 |
15; 41 |
31; 21 |
19; 31 |
19; 41 |
15; 41 |
23; 31 |
23; 51 |
|
|
|
|
|
|
|
|
|
365. |
30; 84 |
40; 114 |
25; 69 |
40; 84 |
45; 114 |
25; 54 |
40; 99 |
30; 69 |
30; 84 |
20; 54 |
30; 84 |
35; 99 |
45; 114 |
35; 84 |
35; 99 |
30; 84 |
25; 69 |
45; 114 |
40; 99 |
35; 99 |
25; 69 |
40; 84 |
30; 69 |
30; 84 |
25; 69 |
30; 69 |
30; 84 |
25; 54 |
30; 84 |
40; 114 |
30; 84 |
35; 99 |
40; 99 |
35; 84 |
35; 114 |
45; 114 |
35; 99 |
40; 84 |
35; 99 |
30; 69 |
30; 84 |
25; 54 |
30; 84 |
25; 69 |
20; 54 |
40; 99 |
30; 69 |
30; 84 |
30; 84 |
30; 99 |
30; 84 |
40; 84 |
30; 69 |
40; 84 |
40; 114 |
30; 84 |
30; 84 |
20; 54 |
30; 84 |
40; 84 |
30; 69 |
30; 84 |
35; 99 |
30; 84 |
25; 69 |
30; 84 |
40; 114 |
35; 99 |
30; 84 |
40; 114 |
30; 99 |
25; 69 |
40; 84 |
30; 84 |
30; 69 |
30; 84 |
40; 84 |
30; 69 |
30; 84 |
40; 99 |
30; 84 |
30; 99 |
45; 114 |
30; 84 |
35; 99 |
25; 54 |
30; 84 |
30; 99 |
30; 84 |
35; 99 |
30; 84 |
25; 54 |
35; 99 |
45; 114 |
30; 84 |
40; 114 |
30; 84 |
40; 84 |
30; 84 |
30; 69 |
|
|
|
|
|
|
|
366. |
69; 79 |
91; 46 |
113; 35 |
80; 68 |
80; 57 |
91; 46 |
80; 57 |
91; 57 |
91; 57 |
80; 57 |
69; 68 |
80; 57 |
91; 57 |
58; 90 |
80; 57 |
113; 24 |
102; 24 |
91; 46 |
102; 24 |
80; 57 |
102; 24 |
69; 68 |
80; 57 |
91; 46 |
80; 57 |
113; 35 |
80; 57 |
91; 57 |
58; 79 |
80; 57 |
91; 46 |
102; 24 |
80; 57 |
69; 79 |
113; 35 |
47; 90 |
80; 57 |
102; 24 |
102; 35 |
80; 79 |
80; 57 |
113; 24 |
80; 57 |
80; 57 |
80; 57 |
91; 57 |
80; 57 |
102; 46 |
80; 57 |
91; 46 |
102; 24 |
80; 68 |
91; 35 |
91; 68 |
113; 35 |
69; 68 |
102; 35 |
91; 57 |
102; 46 |
80; 57 |
102; 35 |
58; 90 |
69; 79 |
91; 68 |
80; 57 |
113; 35 |
69; 68 |
80; 57 |
91; 57 |
80; 57 |
69; 68 |
80; 57 |
58; 79 |
102; 24 |
91; 46 |
80; 57 |
102; 24 |
69; 68 |
102; 35 |
80; 57 |
91; 46 |
80; 57 |
91; 46 |
80; 57 |
91; 57 |
80; 57 |
102; 35 |
80; 57 |
80 ;68 |
113; 35 |
80; 79 |
80; 57 |
102; 24 |
80; 57 |
69; 79 |
80; 57 |
102; 57 |
102; 24 |
91; 46 |
80; 57 |
|
|
|
|
|
|
|
367. |
21;24 |
36;42 |
31;24 |
26;24 |
|||
31;33 |
26;24 |
31;33 |
26;33 |
31;24 |
31;33 |
26;33 |
31;33 |
31;42 |
31;33 |
31;42 |
31;33 |
36;42 |
26;24 |
31;33 |
31;42 |
31;33 |
31;42 |
26;33 |
36;42 |
21;15 |
31;33 |
36;42 |
31;33 |
31;42 |
31;33 |
36;42 |
31;33 |
36;42 |
36;51 |
26;24 |
36;42 |
26;24 |
31;42 |
31;33 |
31;42 |
26;42 |
31;42 |
36;51 |
31;33 |
31;51 |
31;33 |
16;15 |
31;33 |
36;51 |
31;33 |
31;42 |
26;42 |
31;33 |
31;42 |
31;33 |
36;42 |
31;51 |
31;42 |
31;33 |
36;42 |
36;51 |
41;51 |
31;51 |
26;24 |
31;33 |
21;33 |
46;60 |
31;33 |
41;60 |
21;33 |
31;33 |
36;42 |
46;60 |
31;42 |
31;33 |
21;24 |
26;24 |
36;42 |
31;42 |
31;33 |
31;42 |
31;33 |
26;24 |
31;33 |
31;33 |
26;24 |
31;33 |
31;51 |
41;51 |
31;42 |
31;33 |
31;42 |
31;42 |
31;33 |
36;42 |
21;24 |
16;15 |
31;33 |
21;24 |
41;60 |
368. |
36; 47 |
52; 47 |
60; 52 |
60; 57 |
52; 52 |
60; 57 |
36; 42 |
52; 47 |
52; 52 |
60; 52 |
52; 47 |
52; 42 |
60; 57 |
52; 47 |
28; 42 |
52; 47 |
28; 42 |
52; 57 |
52; 47 |
52; 42 |
60; 52 |
36; 42 |
52; 47 |
44; 52 |
52; 47 |
60; 52 |
52; 52 |
52; 47 |
44; 42 |
52; 47 |
52; 52 |
52; 47 |
52; 52 |
52; 47 |
52; 52 |
52; 47 |
44; 42 |
52; 47 |
60; 52 |
52; 52 |
44; 42 |
52; 52 |
60; 57 |
36; 37 |
52; 47 |
60; 52 |
52; 47 |
52; 57 |
44; 47 |
44; 47 |
52; 47 |
60; 52 |
52; 47 |
68; 57 |
44; 42 |
52; 47 |
52; 52 |
44; 42 |
36; 37 |
52; 52 |
60; 52 |
52; 52 |
44; 42 |
52; 57 |
52; 47 |
76; 62 |
36; 42 |
52; 52 |
28; 42 |
36; 37 |
52; 47 |
68; 57 |
52; 47 |
68; 62 |
52; 52 |
44; 42 |
52; 47 |
52; 57 |
52; 47 |
52; 47 |
44; 42 |
52; 52 |
68; 62 |
52; 57 |
52; 47 |
60; 52 |
52; 52 |
36; 57 |
44; 42 |
44; 52 |
52; 47 |
76; 62 |
52; 47 |
44; 47 |
52; 52 |
36; 42 |
52; 47 |
44; 42 |
60; 52 |
52; 47 |
|
|
|
|
|
|
|
|
|
378. |
49;110 |
57;86 |
41;122 |
81;74 |
|||
57; 98 |
49; 110 |
57; 98 |
49;110 |
57;98 |
65;98 |
57;98 |
49;122 |
65; 86 |
57; 98 |
65; 86 |
73;74 |
65;98 |
33;134 |
65;98 |
57;98 |
49;110 |
65;86 |
57;98 |
65;98 |
57;98 |
65;98 |
57;98 |
57;86 |
73;62 |
57;98 |
57;110 |
57;98 |
57;110 |
81;74 |
57;110 |
57;98 |
65;86 |
73;62 |
33;134 |
73;62 |
57;98 |
73;62 |
81;62 |
65;86 |
65;74 |
57;98 |
73;62 |
57;98 |
49;98 |
81;62 |
57;98 |
49;62 |
57;98 |
33;134 |
81;74 |
65;98 |
73;62 |
57;98 |
73;62 |
49;122 |
49;110 |
81;74 |
65;110 |
49;122 |
81;74 |
65;98 |
57;98 |
73;74 |
73;98 |
57;134 |
57;98 |
65;110 |
73;62 |
57;98 |
33;134 |
57;98 |
41;134 |
73;74 |
65;86 |
49;122 |
57;98 |
65;86 |
57;98 |
65;86 |
57;98 |
65;86 |
57;98 |
65;98 |
33;122 |
57;98 |
49;110 |
81;74 |
65; 86 |
73;86 |
41;134 |
73;74 |
33; 122 |
73; 74 |
41; 122 |
73;86 |
379. |
|
|
|
– 4;42 |
– 8;42 |
– 4;42 |
0;48 |
|||
– 4;42 |
– 4;48 |
– 4;42 |
– 4;48 |
– 8;30 |
– 4;42 |
0;48 |
– 8;42 |
|||
0;36 |
– 4;42 |
0;36 |
0;42 |
– 4;42 |
0;42 |
– 8;36 |
– 4;42 |
|||
– 4;42 |
– 8;30 |
– 4;42 |
4;48 |
– 12;30 |
– 4;42 |
4;48 |
– 8;42 |
|||
0;48 |
– 4;42 |
0;42 |
– 4;36 |
– 4;42 |
– 8;42 |
– 4;42 |
0;42 |
|||
– 8;30 |
4;48 |
– 4;36 |
0;42 |
– 4;48 |
0;48 |
– 4;48 |
– 4;42 |
|||
– 4;42 |
– 8;42 |
– 4;42 |
0;54 |
– 8;42 |
– 4;42 |
4;60 |
– 8;36 |
|||
0;54 |
0;42 |
0;54 |
– 12;42 |
– 4;42 |
0;48 |
– 4;42 |
4;54 |
|||
– 4;36 |
– 4;42 |
– 4;36 |
– 4;42 |
– 4;48 |
– 4;42 |
– 4;48 |
– 4;42 |
|||
– 4;42 |
– 8;36 |
– 4;42 |
0;54 |
– 4;42 |
– 8;30 |
– 4;42 |
0;48 |
|||
– 4;48 |
– 4;42 |
0;36 |
– 8;36 |
4;48 |
0;48 |
4;48 |
– 4;48 |
|||
– 4;42 |
– 8;42 |
– 4;42 |
0;48 |
– 4;48 |
– 8;42 |
– 4;42 |
– 8;36 |
|||
– 8;36 |
4;60 |
– 4;36 |
– 4;42 |
–12;24 |
– 4;42 |
– 4;36 |
0;48 |
|||
371. |
3; 78 |
9; 78 |
3; 82 |
0; 82 |
6; 78 |
3; 78 |
6; 78 |
6; 82 |
9; 78 |
9; 74 |
3; 78 |
6; 82 |
3; 82 |
3; 78 |
9; 82 |
0; 82 |
3; 78 |
– 3; 86 |
3; 78 |
3; 78 |
3; 82 |
9; 82 |
3; 78 |
6; 82 |
3; 78 |
– 6; 86 |
6; 78 |
– 3; 86 |
0; 82 |
3; 82 |
9; 78 |
3; 78 |
12; 70 |
3; 78 |
3; 82 |
9; 78 |
3; 78 |
3; 78 |
3; 78 |
– 6; 86 |
3; 78 |
6; 82 |
3; 78 |
9; 82 |
3; 78 |
0; 86 |
– 6; 86 |
9; 78 |
9; 78 |
12; 70 |
3; 82 |
0; 82 |
3; 82 |
3; 78 |
6; 82 |
3; 78 |
12; 74 |
3; 78 |
6; 78 |
3; 78 |
6; 78 |
3; 78 |
6; 82 |
0; 82 |
9; 74 |
3; 82 |
3; 78 |
12; 74 |
0; 82 |
6; 78 |
3; 78 |
9; 74 |
3; 78 |
6; 82 |
3; 78 |
3; 78 |
6; 78 |
0; 78 |
3; 82 |
0; 82 |
3; 82 |
3; 78 |
6; 78 |
3; 78 |
6; 82 |
9; 78 |
3; 78 |
3; 82 |
3; 78 |
9; 74 |
9; 78 |
0; 78 |
3; 78 |
12; 74 |
3; 86 |
3; 78 |
3; 86 |
6; 82 |
9; 78 |
6; 78 |
|
|
|
|
|
|
|
|
|
372. |
15; 27 |
18; 35 |
18; 27 |
18; 31 |
21;31 |
15;31 |
18; 31 |
15; 27 |
21; 31 |
21; 35 |
15; 23 |
18; 31 |
15; 27 |
27; 39 |
12; 23 |
18; 31 |
18; 35 |
18; 31 |
12; 27 |
18; 31 |
24; 35 |
15; 31 |
12; 27 |
18; 27 |
15; 31 |
27; 41 |
15; 23 |
18; 31 |
24; 35 |
21; 31 |
15; 27 |
21; 35 |
18; 27 |
15; 31 |
21; 35 |
15; 27 |
18; 27 |
24; 35 |
15; 23 |
15; 23 |
24; 39 |
18; 31 |
15; 31 |
15; 23 |
18; 27 |
27; 39 |
18; 31 |
9; 15 |
15; 27 |
18; 27 |
12; 19 |
24; 35 |
18; 27 |
27; 39 |
15; 31 |
18; 35 |
24; 39 |
18; 31 |
18; 27 |
15; 27 |
18; 31 |
18; 27 |
15; 27 |
18; 31 |
18; 27 |
12; 23 |
18; 31 |
18; 35 |
12; 23 |
18; 27 |
15; 31 |
21; 31 |
18; 31 |
24; 39 |
15; 27 |
18; 35 |
15; 27 |
15; 31 |
18; 31 |
15; 23 |
21; 35 |
12; 23 |
24; 35 |
18; 31 |
18; 35 |
15; 23 |
21; 39 |
18; 27 |
18; 31 |
21; 35 |
18; 31 |
21; 35 |
18; 31 |
12; 19 |
18; 27 |
18; 27 |
18; 31 |
12; 27 |
18; 27 |
18; 31 |
|
|
|
|
|
|
|
|
|
373. |
26; 37 |
26; 23 |
26; 30 |
26; 30 |
26; 37 |
16; 27 |
26; 30 |
31; 37 |
21; 30 |
11 9 |
26; 37 |
31; 30 |
31; 37 |
26; 23 |
21; 30 |
36; 37 |
21; 16 |
16;16 |
26; 23 |
21; 23 |
21; 30 |
26; 30 |
21; 23 |
11; 2 |
31; 30 |
26; 30 |
36; 44 |
21; 30 |
21; 16 |
26; 30 |
31; 37 |
21; 16 |
26; 30 |
31; 37 |
26; 23 |
41; 44 |
21; 30 |
26; 30 |
21;23 |
16; 27 |
26; 30 |
31; 37 |
26; 37 |
26; 30 |
16; 16 |
26; 30 |
36; 37 |
21; 23 |
31; 37 |
26; 30 |
21; 23 |
26; 30 |
21; 23 |
36; 37 |
26; 30 |
21; 23 |
26; 30 |
26; 23 |
31; 30 |
21; 16 |
31; 30 |
16; 16 |
26; 30 |
21; 30 |
41; 44 |
26; 23 |
16; 9 |
26; 23 |
21; 30 |
26; 23 |
26; 30 |
26; 23 |
31; 44 |
36; 44 |
21; 16 |
26; 37 |
26; 23 |
26; 23 |
11; 9 |
21; 30 |
16; 9 |
36; 37 |
16; 27 |
26; 23 |
36; 37 |
21; 23 |
41; 51 |
26; 30 |
21; 30 |
26; 30 |
26; 23 |
21; 16 |
26; 23 |
26; 30 |
26; 30 |
21; 16 |
26; 23 |
16; 16 |
21; 23 |
21; 23 |
|
|
|
|
|
|
|
|
|
374. |
32; 44 |
26; 36 |
32; 52 |
26; 44 |
26; 44 |
32; 52 |
20; 28 |
32; 52 |
26; 44 |
38; 44 |
32; 36 |
38 ;44 |
32; 44 |
20; 36 |
38; 52 |
32; 52 |
32; 44 |
32; 44 |
14; 28 |
26; 36 |
38; 44 |
14; 28 |
38; 52 |
32; 44 |
32; 44 |
26; 44 |
38; 52 |
44; 52 |
32; 44 |
44; 52 |
26; 44 |
44; 52 |
26; 36 |
38; 52 |
50; 60 |
44; 60 |
20; 36 |
32; 44 |
8; 12 |
32; 36 |
32; 44 |
20; 28 |
38; 52 |
26; 44 |
14; 28 |
32; 44 |
32; 52 |
20; 28 |
32; 52 |
32; 44 |
38; 44 |
38; 52 |
26; 36 |
32; 52 |
32; 44 |
44; 60 |
32; 44 |
32; 44 |
20; 28 |
26; 44 |
8; 20 |
32; 44 |
32; 44 |
44; 60 |
32; 44 |
14; 20 |
32; 52 |
26; 44 |
32; 52 |
44; 52 |
32; 52 |
38; 44 |
38; 44 |
20; 36 |
44; 60 |
32; 44 |
38; 52 |
32; 36 |
26; 44 |
20; 36 |
32; 52 |
26; 36 |
26; 44 |
32; 52 |
32; 44 |
38; 52 |
20; 28 |
14; 20 |
32; 44 |
38; 44 |
26; 36 |
44; 52 |
38; 52 |
26; 44 |
38; 52 |
26; 44 |
44; 52 |
32; 36 |
20; 36 |
32; 44 |
|
|
|
|
|
|
|
|
|
375. |
13; 24 |
16; 24 |
10; 28 |
16; 24 |
16; 24 |
19; 24 |
7; 32 |
13; 24 |
19; 24 |
16; 24 |
10; 28 |
19; 24 |
16; 24 |
19; 24 |
13; 24 |
19; 20 |
16; 24 |
19; 20 |
13; 32 |
7; 36 |
16; 24 |
16; 24 |
19; 24 |
16; 24 |
16; 24 |
13; 28 |
19; 24 |
16; 24 |
22; 20 |
16; 24 |
16; 20 |
10; 32 |
16; 24 |
4; 36 |
19; 24 |
19; 16 |
13; 24 |
19; 24 |
16; 28 |
19; 24 |
13; 28 |
16; 24 |
16; 24 |
16; 28 |
16; 24 |
19; 24 |
19; 20 |
16; 28 |
19; 24 |
10; 28 |
19; 24 |
13; 24 |
22; 16 |
16; 24 |
19; 16 |
13; 32 |
16; 24 |
16; 24 |
13; 28 |
22; 20 |
16; 24 |
25; 12 |
10; 32 |
22; 16 |
16; 24 |
19; 24 |
22; 20 |
22; 20 |
16; 24 |
13; 24 |
22; 12 |
16; 28 |
25; 16 |
13; 28 |
13; 24 |
16; 24 |
13; 28 |
16; 24 |
16; 28 |
19; 24 |
7; 32 |
25; 16 |
13; 24 |
16; 24 |
22; 16 |
16; 24 |
19; 24 |
13; 24 |
16; 24 |
13; 32 |
16; 24 |
13; 24 |
19; 16 |
16; 24 |
10; 32 |
22; 16 |
16; 24 |
16; 28 |
13; 32 |
16; 20 |
|
|
|
|
|
|
|
|
|
376. |
44; 15 |
44; 22 |
29; 36 |
34; 22 |
39; 22 |
49; 15 |
44; 22 |
49; 15 |
34; 29 |
49; 15 |
39; 29 |
49; 15 |
44; 22 |
39; 15 |
44; 15 |
29; 29 |
49; 15 |
39; 22 |
39; 15 |
39; 22 |
44; 15 |
44; 22 |
39; 22 |
49; 8 |
44; 22 |
39; 15 |
39; 22 |
44; 22 |
39; 22 |
44; 22 |
49; 8 |
39; 22 |
49; 15 |
39; 22 |
44; 22 |
44; 15 |
44; 22 |
39; 15 |
44; 15 |
59; 1 |
44; 22 |
39; 22 |
39; 15 |
49; 15 |
44; 22 |
39; 22 |
49; 8 |
29; 36 |
44; 15 |
34; 22 |
44; 15 |
49; 15 |
44; 15 |
39; 22 |
44; 15 |
49; 15 |
39; 22 |
49; 8 |
39; 22 |
59; 8 |
44; 22 |
39; 15 |
39; 29 |
54; 8 |
29; 29 |
44; 22 |
44; 15 |
44; 22 |
49; 15 |
39; 22 |
59; 8 |
24; 36 |
54; 8 |
44; 15 |
44; 15 |
49; 8 |
44; 22 |
49; 15 |
39; 29 |
59; 8 |
39; 22 |
59; 8 |
39; 15 |
39; 22 |
44; 22 |
39; 15 |
44; 15 |
44; 15 |
39; 15 |
44; 22 |
54; 8 |
34; 22 |
49; 15 |
44; 15 |
54; 8 |
44; 22 |
39; 15 |
34; 22 |
34; 29 |
39; 29 |
44; 15 |
|
|
|
|
|
|
|
|