Порядок выполнения работы

Студенты получают задание с исходными данными для расчета и установления математической модели распределения погрешностей измерений определения концентрации вредного вещества в окружающей среде. Работу выполняют в несколько этапов:

1. Изучают основные теоретические положения и выбирают одну из оценок центра распределения погрешностей;

2. Производят графическое построение математической модели распределения погрешностей и определяют ее характеристики;

3. Сравнивают экспериментальные и теоретические модели распределения погрешностей и выбирают закон распределения;

4. Производят проверку соответствия эмпирического распределения выбранной модели.

Пример

По данным многократных наблюдений концентрации вредных веществ выборка объемом n = 80 со значениями от 4,92 до 5,16.

На основании формул (1), (2), (11), (14), (15) определяют оценки параметров и характеристик эмпирического распределения погрешностей: = 5,0168; σ = 0,045; k = 0,54; Х_г— = 4,879; Х_г+ = 5,155.

Значение 5,16 является промахом на основании (15), а поэтому после исключения его из вариационного ряда получили:

n = 79; = 5,015; Ме = 5,020; Х_г— = 4,893; Х_г+ =5,1317; σ = 0,042; γ_а = -0,33; 1,5σ(γ_а) = 0,4; γ_э = -0,14; k = 0,59; Δ = 0,079; K = 1,87; m = 7 (6,07); d = 0,027.

Так как | γ_а | < 1,5 σ(γ_а), т.е. 0,33 < 0,4, эмпирическое распределение погрешностей считают симметричным и выбор математической модели осуществляют для симметричных функций.

Графическое представление эмпирического распределения погрешностей в виде гистограммы и полигона показано на рис. 2. Количество интервалов группирования значений выборки определяется по формуле (20)

Полученное значение округляют до большего нечетного числа m = 7.

На основании сравнения оценок параметров и характеристик эмпирического распределения погрешностей с их числовыми значениями для математических моделей табл. 26 [5]) выбирают две теоретические функции – нормальную (рис. 2, б) и треугольную (рис. 2, в) в качестве аппроксимирующих данное эмпирическое распределение погрешностей для дальнейшей проверки их по критериям согласия. Вычисляют значения теоретических вероятностей и заносят данные в табл. 3.

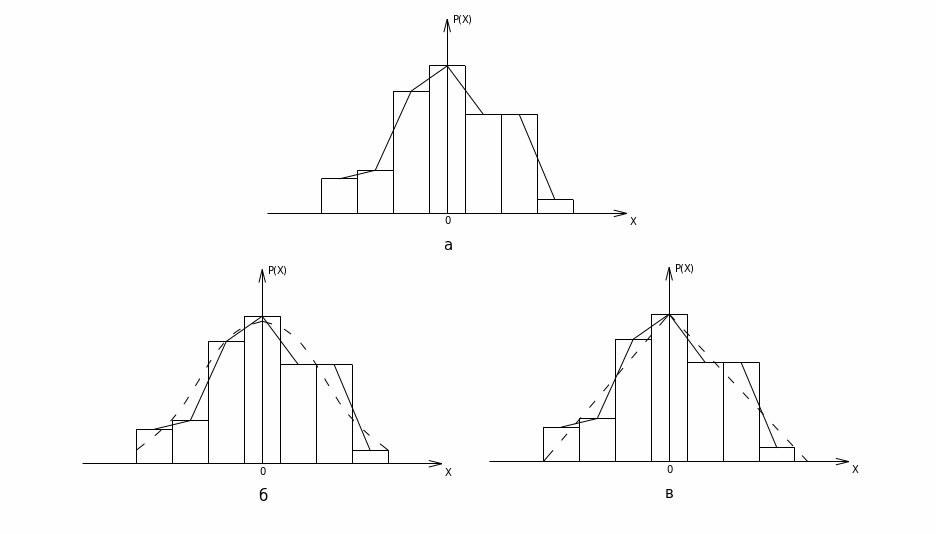Рис. 2. Графическое представление эмпирического распределения

Таблица 3

Расчетные данные

Номер интервала	Середина интервала	Эмпиричес­кая частость	Вероятность		Теоретическая частость
			Нормальная функция	Треуголь­ная функция	Нор- мальная функция	Тре- угольная функция
1	4,9336	5	0,04	0,055	3,13	4,37
2	4,9607	6	0,112	0,125	8,85	9,85
3	4,9879	17	0,209	0,194	16,51	15,32
4	5,0150	21	0,257	0,263	20,32	20,8
5	5,0421	14	0,209	0,194	16,51	15,32
6	5,0693	14	0,112	0,125	8,84	9,85
7	5,0963	2	0,04	0,055	3,13	4,37

Проверку согласия эмпирического распределения с выбранными теоретическими функциями (нормальной и треугольной) проводят по критерию ω²:

(ω_n²)_норм = 3,87; (ω_n²)_треуг = 1,07.

После этого задают уровень значимости q = 0,1. По прил. 3 находят значение функции α (ω_n²), соответствующее вычисленному значению ω_n². Значения ω_n² в прил. 3 ограничены значением 2,5. При (ω_n²)_норм > 2,5 значение функции α(ω_n²)_норм > 0,95 и стремится к единице. При (ω_n²)_треуг = 1,07 α(ω_n²)_треуг будет равно 0,673. При заданном уровне значимости q = 0,1 α (ω_n²)_треуг = 0,673 > > (1 - 0,1).

Таким образом, принимают гипотезу о законе распределения Симпсона. Математическая модель эмпирического распределения погрешностей имеет вид

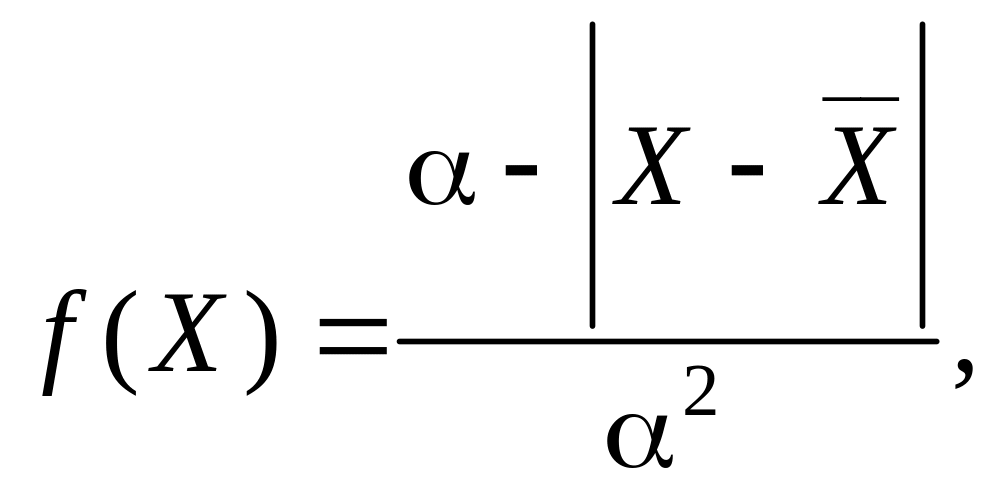
где α = σ .