Формулы для определения начальных и центральных моментов

αк	μk	μk = f (αk)
		;
		μ2 = α2 – α12
		μ3 = α 3 – 3 α 2 α 1 + 2 α 13
		μ4 = α4 – 4 α 3 α 1 + 6 α 2 α 12 – – 3 α 14

3. Определяют параметры рассеивания погрешностей. Несмещенную оценку дисперсии и среднего квадратического отклонения определяют по формулам:

(10)

. (11)

4. Определяют параметры островершинности распределения погрешностей. Эксцесс определяют по формуле

(12)

Коэффициент эксцесса определяют по формуле

γ_э = μ₄/σ⁴ + 3. (13)

Контрэксцесс определяют по формуле

(14)

где 0 < k < 1.

5. Определяют границы промахов. Промахами (грубыми погрешностями) считают погрешности, отклонения которых от центра распределения существенно превышают значения, оправданные объективными условиями измерения, и для которых выполняются неравенства Х_г— > Х_i и Х_г+ < Х_i, где Х_г— и Х_г+ - границы промахов, определяемые из выражения

, (15)

где – центр распределения погрешностей, определенный в зависимости от значения k.

После исключения из выборки промахов повторяют вычисления по пп. 1–5.

6. Определяют параметры асимметрии распределения погрешностей. Коэффициент асимметрии распределения погрешностей определяют по формуле

(16)

Среднее квадратическое отклонение коэффициента асимметрии определяют по формуле

(17)

Распределение погрешностей симметрично, если выполняется условие

(18)

7. Определяют показатель формы распределения погрешностей. Показатель формы распределения погрешностей измерения связан с эксцессом Э функциональной зависимостью

(19)

и определяется по графику зависимости показателя формы α от эксцесса Э, представленному на рис. 1.

8. Графически представляют статистические данные. Законы распределения погрешностей измерения и средств измерений определяют экспериментально на основании статистических данных.

Допустим, определяется закон распределения погрешности измерения или средства измерений при ручной обработке информации. Гистограмма (ступенчатый многоугольник, служащий для наглядного представления об эмпирическом распределении и оценки качества произведенного группирования), являющаяся ступенчатой аппроксимацией плотности вероятностей погрешностей, строится в следующем порядке:

1) значения погрешностей располагают в вариационный ряд Х₁; Х₂; …; Х _S ; …; Х_n, где Х _S-1 ≤ Х_S ≤ Х _S+1;

a

Э

Рис. 1. Зависимость показателя формы α от эксцесса Э

2) определяют число интервалов группирования погрешностей, используя вычисленное значение контрэксцесса k:

(20)

Значение m округляют до большего нечетного числа;

3) определяют ширину интервала группирования:

(21)

4) группируют погрешности по интервалам:

(22)

где Г_j - левая граница j-го интервала группирования (j = 1, 2, …, m);

5) определяют вероятность р_i попадания погрешностей в j-й интервал группирования:

(23)

где j = 1, 2, …, m.

Сумма вероятностей по всем интервалам равна

(24)

На каждом интервале, как на основании, строят прямоугольник, площадь которого равна вероятности этого интервала, высота – вероятности, деленной на ширину интервала. Масштаб графика выбирают таким образом, чтобы отношение высоты гистограммы к ее основанию составляло примерно 0,6.

Полигон (ломаную линию) распределения погрешностей строят, соединяя середины верхних сторон прямоугольников гистограммы. Гистограмме обычно отдают предпочтение, потому что ее площадь всегда равна объему выборки, а площадь под полигоном этим качеством не обладает.

Гистограмма или полигон может иметь не одну, а две или несколько вершин, наличие которых трудно объяснить случайными колебаниями. Тогда следует предположить, что вариационный ряд составлен при существенно разных условиях. В этом случае тщательно анализируют условия наблюдения.

9. Определяют информационные характеристики распределения погрешностей. Энтропийное значение погрешности определяют по формуле

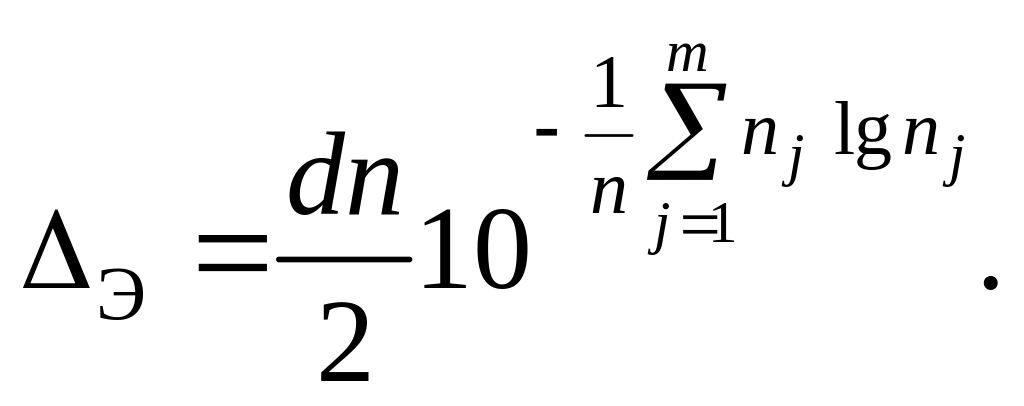(25)

Энтропийный коэффициент, определяющий форму вершины распределения погрешностей, определяют по формуле

(26)

На основании вида гистограммы и полигона, а также сравнения оценок параметров и характеристик эмпирического распределения погрешностей: Э; γ_э; k; γ_а; σ (γ_а); α с их критериальными значениями, приведенными в табл. 26 [5], выдвигают одну или несколько гипотез о виде математической модели эмпирического распределения погрешностей.

На основании гипотез последовательно производят вычисление теоретических плотностей распределения вероятностей погрешностей и теоретических частот следующим образом. Подставляют значения параметров табл. 26 [5] в математическую модель распределения погрешностей и, умножая полученные значения на ширину интервала группирования d, определяют плотность распределения вероятностей погрешности f (X) для значений Х_j (i = 1, 2, …, m), равных серединам интервалов группирования. Теоретические частоты n_i определяют в каждом интервале группирования, умножая вычисленные значения плотности распределения погрешностей f (X _i) на объем выборки n.

После этого проверяют соответствие эмпирического распределения погрешностей выбранной математической модели. Проверку производят в зависимости от объема выборки. Для объемов выборок 50 > n > 15 проверку проводят по составному критерию, для объемов выборок 50 < n < 200 проверку на соответствие эмпирического распределения математической модели проводят по критерию Мизеса – Смирнова (ω²), для выборки с n > 100 рассчитывают критерий Пирсона (²).

Составной критерий состоит из двух составляющих.

Критерий 1. Определяют значение отношения по формуле

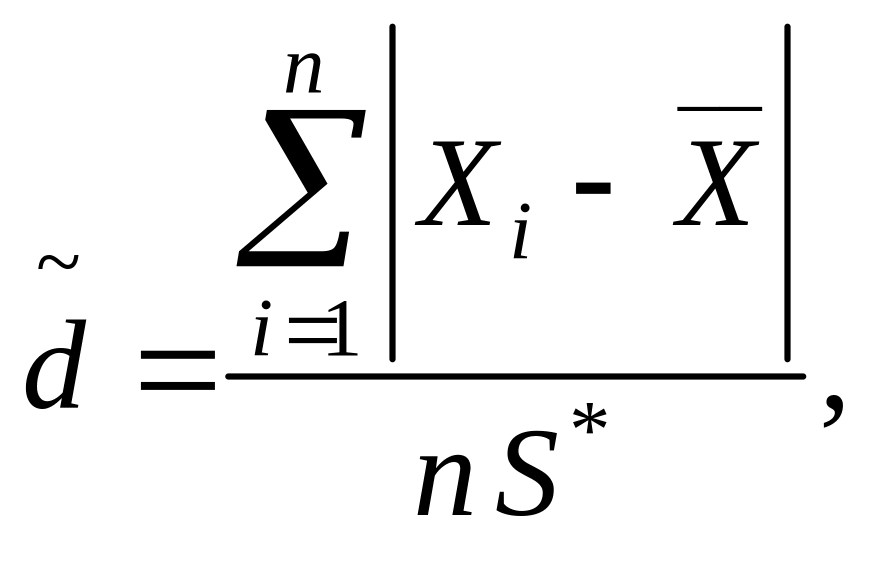(27)

где S^* - смещенная оценка среднего квадратического отклонения, вычисляемая по формуле

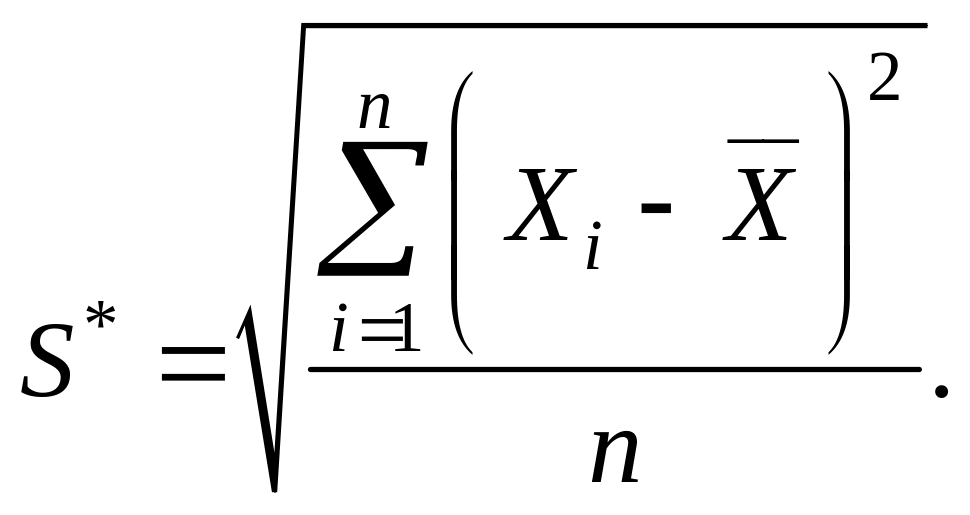(28)

Распределение результатов наблюдений считают нормальным, если

(29)

где и – квантили распределения, определяемые в соответствии с прил. 1 по n, q₁/2 и (1 - q₁/2), причем q₁ – заранее выбранный уровень значимости критерия.

Критерий 2. Результаты наблюдений считают нормальными, если не более m разностей (Х_i - ) превзошло значение Z_P/2 S, где Z_P/2 – верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности Р/2; S – оценка среднего квадратического отклонения, вычисляемая по формуле

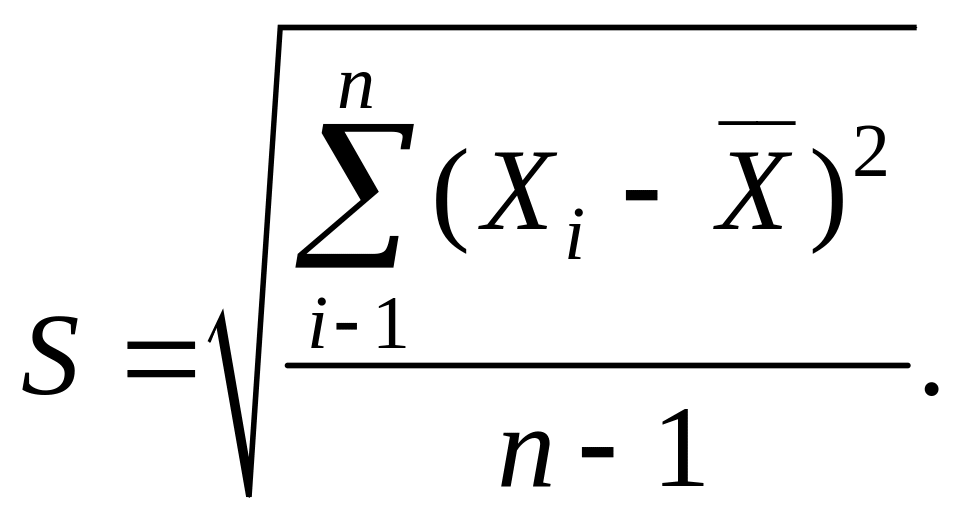(30)

Значения Р определяют в соответствии с прил. 2 по выбранному уровню значимости q₂ и числу результатов наблюдений n.

Если при проверке соответствия опытных данных теоретичес­ким для критерия 1 выбран уровень значимости q₁, а для критерия 2 – q₂, то результирующий уровень значимости составного критерия равен q = q₁ + q₂. Если хотя бы один из критериев не соблюдается, то гипотеза о теоретическом распределении отвергается.

Вычисления критерия Мизеса – Смирнова проводят в следующем порядке.

Определяют значение ω_n² по формуле

(31)

где Х_i (i = 1, 2, …, n) – результат наблюдений, имеющий i-й номер в вариационном ряду Х₁ ≤ Х₂ ≤ … ≤ Х_n; F (X_i) – значение функции теоретического распределения при значении аргумента Х_i, равное

(32)

где f (X_i) – плотность вероятности функции распределения.

Результаты, полученные по формуле (31), сводят в табл. 2. Вычисления проводят с точностью до пяти значащих цифр, округляя окончательный результат до двух значащих цифр. Заполнив табл. 2, получают значение ω_n² путем суммирования чисел, занесенных в графу 10 табл. 2. Затем по прил. 3 находят значение функции α(ω_n²), соответствующее вычисленному значению ω_n². Функция α(ω_n²) представляет собой функцию распределения величины ω_n².

После этого задают уровень значимости α, равный 0,1 или 0,2. Если α(ω_n²) ≥ (1 – α), то гипотезу о согласии эмпирического и теоретического распределений отвергают. Если α(ω_n²) < (1 – α), то гипотезу принимают.

Если для нескольких математических моделей нет существенного расхождения с эмпирическим распределением погрешнос­тей, то в качестве математической модели принимают ту из них, для которой получена наибольшая вероятность согласия.