Прямое уравнение Колмогорова. Уравнение Фоккера-Планка

Теперь получим прямое уравнение Колмогорова, которое является сопряжённым к обратному и ещё называется уравнением Фоккера-Планка. Для вывода этого уравнения необходимо существование переходной плотности распределения, так как прямое уравнение составлено именно для переходной плотности распределения p(s,x;t,y).

Теорема. Если для переходной плотности распределения p(s,x;t,y) существуют производная по t, а также первая и вторая производные по y, то для любых y и всех t>s переходная плотность распределения p(s,x;t,y) удовлетворяет уравнению

,

которое называется прямым уравнением Колмогорова или уравнением Фоккера-Планка.

Некоторые частные случаи уравнения Фоккера-Планка

Рассмотрим некоторые частные случаи уравнения Фоккера-Планка.

1. Для однородного диффузионного процесса

,

а переходная плотность распределения вероятностей p(s,x;t,y) зависит лишь от разности моментов времени, то есть имеет вид

,

поэтому уравнение Фоккера-Планка примет вид

с начальным условием .

Если при  существует предел

,

не зависящий от x, то функцию p(y) называют финальной или стационарной плотностью распределения вероятностей значений однородного диффузионного процесса.

Для стационарной плотности распределения уравнение Фоккера-Планка примет вид

,

который получается если положить p(t,y)p(y). Решение этого уравнения не представляет труда, так как оно относится к классу обыкновенных линейных дифференциальных уравнений первого порядка

,

где C₁ – произвольная постоянная, полученная в результате интегрирования исходного уравнения.

2. Рассмотрим диффузионный процесс авторегрессии, для которого коэффициенты переноса и диффузии имеют вид a(y)=-y, b(y)=², тогда уравнение предыдущее уравнение при C₁=0 перепишем следующим образом

.

Его решение, удовлетворяющее условию нормировки, запишем в виде

,

то есть решением p(y) этого уравнения является плотность нормального распределения с нулевым математическим ожиданием и дисперсией равной .

3. Винеровским диффузионным процессом будем называть однородный диффузионный процесс с коэффициентами переноса и диффузии вида a(y)=0 b(y)=², тогда уравнение Фоккера-Планка примет вид

.

Решение этого уравнения выполним методом характеристических функций

.

Домножив левую и правую части этого уравнения на e^iuy и проинтегрировав их по y(–,), получим равенство

.

Здесь

,

.

Поэтому можно записать

,

то есть в виде обыкновенного линейного дифференциального уравнения первого порядка, решение которого, удовлетворяющее начальному условию

,

имеет вид

,

то есть вид характеристической функции нормального распределения с математическим ожиданием равным x и дисперсией равной ², следовательно, переходная плотность распределения вероятностей p(x,,y) имеет вид

.

Допредельная модель диффузионного процесса

Рассмотрим реальные процессы, которые достаточно хорошо описываются диффузионными случайными процессами.

Представим себе частицу, совершающую скачкообразные движения по оси X. За время t частица совершает скачок на величину  с вероятностью 1/2, при этом скачки выполняются независимо друг от друга. Через (T) обозначим координату частицы в момент времени T, через x_k – величину скачка частицы в k-й момент времени. Здесь x_k= с вероятностью 1/2. Очевидно, что

.

Найдём среднее значение и дисперсию положения частицы в момент времени T

,

.

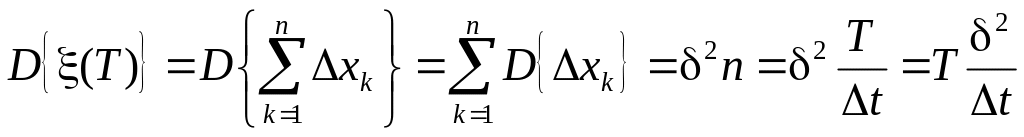В пределе, при t0, 0, возможны три варианта.

а) Если ²=(t), то D(T)0, а так как M(T)=0, то частица не меняет своего положения, оставаясь в начальной точке. Этот случай не представляет интереса.

б) Если t=(²), то D(T), следовательно, положение частицы в конечный момент времени T имеет бесконечный разброс, что для реальных процессов невозможно, поэтому такой вариант рассматривать не будем.

в) Если ²=(t), то есть эти величины одного порядка малости, например ²=Bt, где B>0 – некоторая постоянная, тогда D(T)=B. Этот вариант рассмотрим более подробно.

Рассмотрим приращения

,

для которых можно записать

,

.

Тогда в силу центральной предельной теоремы можно записать

,

и все приращения по предположению независимы. Следовательно, рассматриваемое случайное блуждание в пределе даёт винеровский процесс.

Остановимся на особенностях траекторий винеровского процесса. Так как при t0, величина скачка 0, , то реализации винеровского процесса непрерывны.

С другой стороны, отношение

,

то есть производная не существует, поэтому говорят, что реализации винеровского процесса недифференцируемы.

Таким образом, случайное блуждание частица, при достаточно малой величине скачка, можно описать винеровским процессом, то есть диффузионным процессом с коэффициентами переноса, равным нулю, и коэффициентом диффузии, равным некоторой положительной постоянной.

Более общий вариант диффузионного процесса можно получить в пределе, если пролагать, что положительный скачок происходит с вероятностью ½+, а отрицательный – с вероятностью ½–. Тогда

,

.

Так как , то

.

Полагая, что , получим

.

При этом

.

Нетрудно показать, что при t0 в пределе несимметричное блуждание переходит в диффузионный процесс с коэффициентом переноса – A, и коэффициентом диффузии – B.