Контрольное задание 9.

1. Вычислить криволинейный интеграл , где L – линия пересечения верхней полусферы с цилиндром . L пробегает против хода часовой стрелки, если смотреть из точки (0,0,3R).

2. Найти циркуляцию векторного поля вдоль замкнутого контура L, составленного из части винтовой линии и отрезка прямой, соединяющей точки B(a,0,2π) и A(a,0,0). Движение происходит от точки B к A и далее к B.

3. Для векторного поля вычислить , циркуляцию поля вдоль окружности и выяснить, является ли поле потенциальным в области ; в области ?

4. Найти циркуляцию поля вдоль контура треугольника OABO c координатами вершин O(0,0,0), A(1,1,2), B(0,1,2). Ответ проверить с помощью формулы Стокса. Найти максимальное значение циркуляции по данному контуру.

§11. Операторы Гамильтона и Лапласа.

Определение 13. Оператором Гамильтона называют символический вектор (набла): или .

С помощью оператора Гамильтона можно кратко записывать операции над скалярными и векторными полями, доказывать некоторые утверждения векторного анализа. Данный оператор имеет и самостоятельное значение.

Операции первого порядка:

1. Умножая вектор на скалярную функцию , получим :

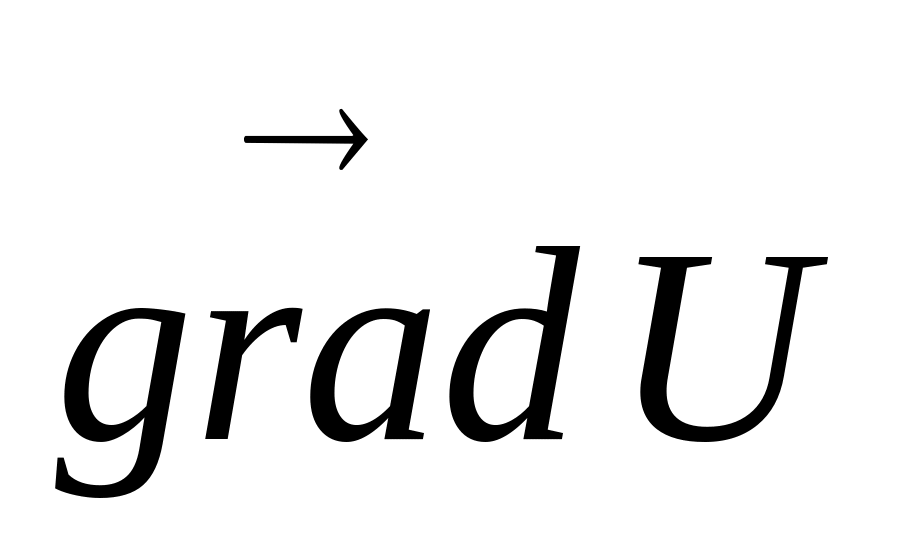2. Скалярное произведение вектора на вектор-функцию даёт : .

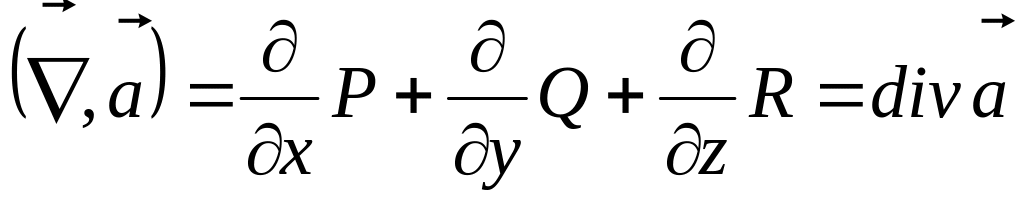3. Векторное произведение вектора на вектор-функцию даёт :

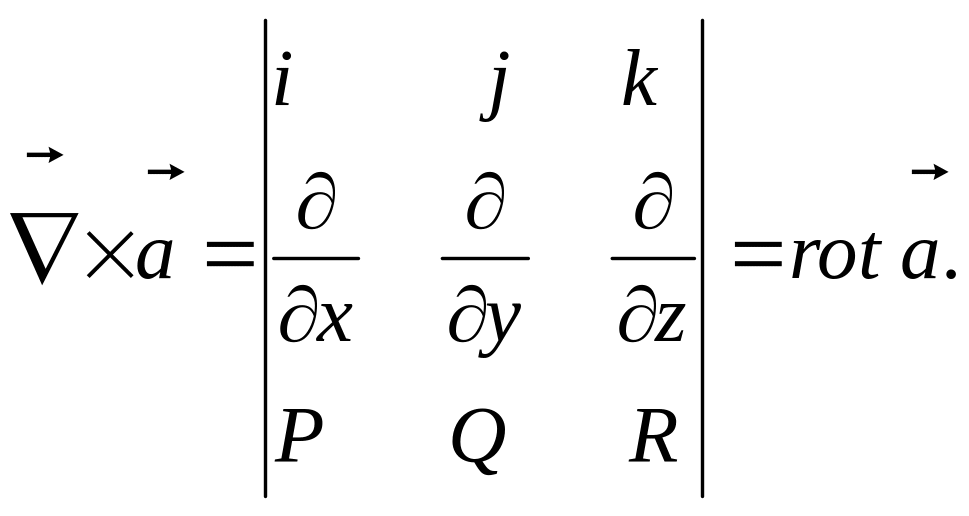
Применять оператор нужно, соблюдая следующие правила:

1. Линейность оператора . Пусть 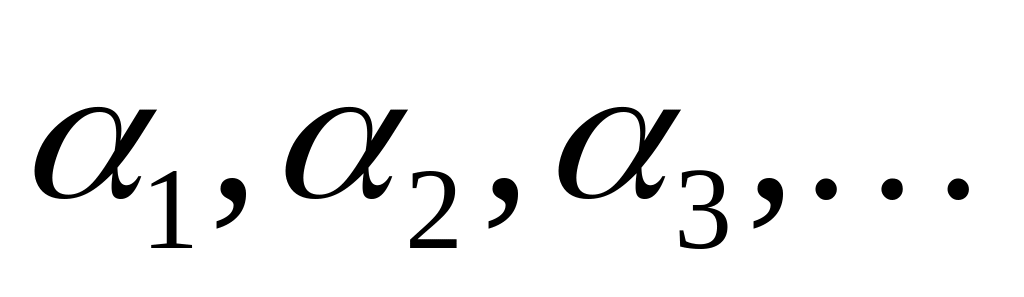- вещественные или комплексные числа, 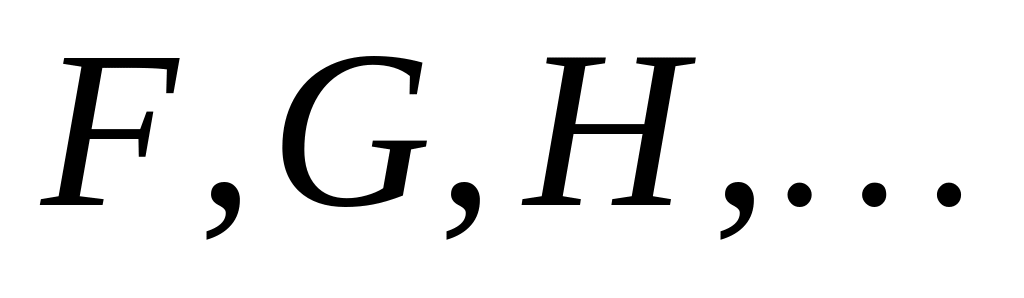- скалярные или векторные функции. Тогда

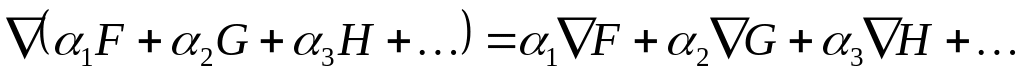
2. Действие оператора на произведение функций. .

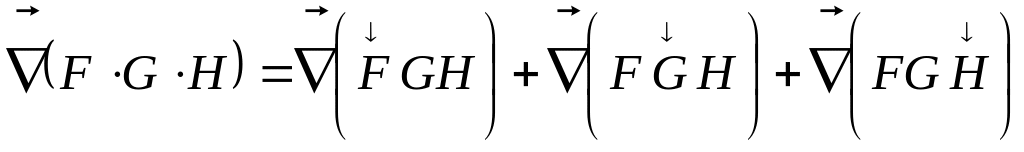(Символ «↓» указывает на объект действия оператора).

Докажем, например, что .

.

При доказательстве воспользовались свойством смешанного произведения векторов .

Дифференциальные операции второго порядка.

Пусть в области G заданы скалярное поле и векторное поле , такие, что функции имеют в области G непрерывные частные производные второго порядка. Тогда и - дифференцируемые векторные поля, - дифференцируемое скалярное поле. В этих случаях к полям и применимы операции вычисления дивергенции и ротора, а к полю - операция вычисления градиента. Таким образом, получим пять повторных операций:

, , , , .

Определение 14. Операция называется оператором Лапласа и обозначается символом (лапласиан): . Оператор Лапласа можно записать с помощью оператора набла : .

При этом . Тогда

Определение 15. Уравнение в частных производных или называют уравнением Лапласа.

Дважды дифференцируемую функцию , удовлетворяющую этому уравнению, называют гармонической в области G. Для плоской области уравнение Лапласа примет вид: .

Примеры гармонических функций: , , .

Запись дифференциальных операций второго порядка в операторной форме.

- потенциальное поле является безвихревым полем.

- векторное поле роторов соленоидально.

=

,где - вектор-функция, полученная в результате применения оператора Лапласа функциям .

Определение 16. Векторное поле называется гармоническим в области G, если в этой области оно одновременно является потенциальным и соленоидальным, т.е. для любой точки гармонического поля выполняются условия и . Для односвязных областей из первого условия следует, что , а из второго, что , т. е. функция φ, потенциал поля – решение уравнения Лапласа и гармоническая функция.

Пример 27. Проверить гармоничность функции .

функция - гармоническая. Тогда поле - гармоническое и , .

Пример 28. Доказать формулу .

Доказательство. При этом . Тогда , ч. т. д.

Пример 29. Найти .

Решение. С помощью оператора имеем: .