Контрольное задание 6.

1. Проверить, что векторное поле потенциально. Найти его потенциал. Изобразить линии равного потенциала. Найти векторные линии и изобразить их на том же рисунке. Вычислить работу поля при перемещении материальной точки от точки до . Найти векторную линию и эквипотенциальную линию, проходящую через точку .

2. Проверить, является ли векторное поле потенциальным. Если да, найти его потенциал.

3. Найти потенциал гравитационного поля .

4. Показать, что векторное поле потенциально и найти его потенциал.

§8. Поток векторного поля.

Пусть σ – некоторая ориентированная поверхность в области G. Выберем определённую её сторону, задав единичный вектор нормали к поверхности .

Определение 9. Потоком вектора через поверхность σ называется поверхностный интеграл от скалярного произведения вектора поля на нормальный единичный вектор: П . (13)

Имеют место другие формы записи потока вектора. Например, учитывая, что Пр получим: П .

Или можно определить вектор , направленный по нормали к поверхности, такой, что: , . Тогда: . (14)

Если поверхность σ замкнута, то обычно за направление вектора берут направление внешней нормали к поверхности и обозначают

. (15)

Если изменить ориентацию (взять другую сторону поверхности), то скалярное произведение и, соответственно, поток меняют знак.

Поток можно записать в координатной форме, представив соответствующим образом скалярное произведение векторов и :

. (16)

Или , (17)

где в правой части имеем поверхностный интеграл второго рода.

Каждое из слагаемых в формуле (17) преобразуется в двойной интеграл по области D, являющейся проекцией поверхности σ на соответствующую координатную плоскость:

(18)

где - проекции σ на координатные плоскости Oyz, Oxz, Oxy соответственно. Знак перед двойным интегралом в правой части совпадает со знаком косинуса угла между нормальным вектором к поверхности и положительным направлением осей Ox, Oy, Oz соответственно. Выражения получают, выражая переменные из уравнения поверхности σ: . Можно свести вычисление потока к вычислению интеграла первого рода, подставив в формулу (16) , , .

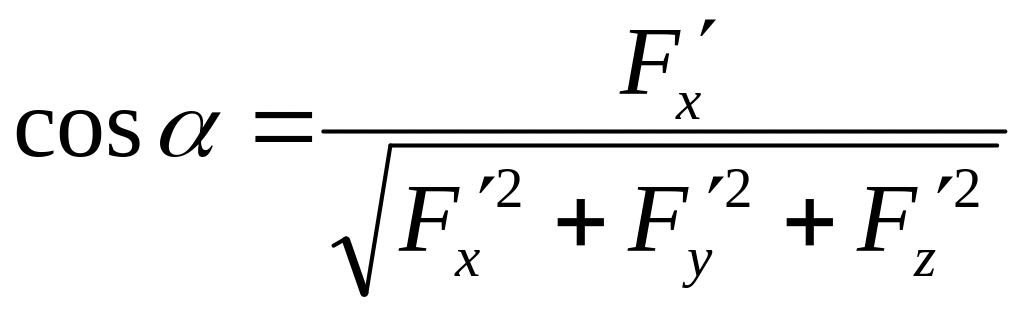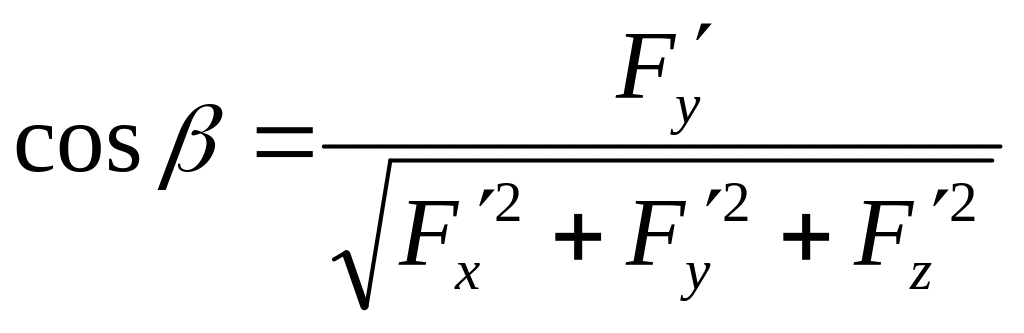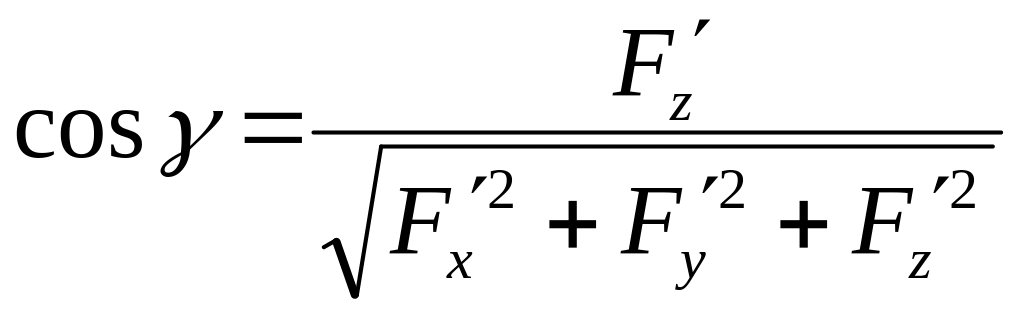Пример 16. Вычислить поток векторного поля через часть плоскости , заключённую в первом октанте, в сторону нормали, составляющей тупой угол с осью OY.

Р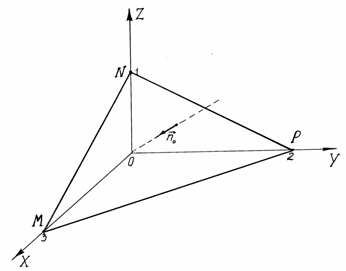 ешение.

По формуле (13) , где σ – плоскость S: .

В

Рисунок 12

спомним, что нормальный вектор к плоскости с уравнением имеет вид . В нашей задаче , этот вектор составляет острый угол с осью OY. Тогда .

Сведём задачу к вычислению интеграла I рода (см. (13)).

, .

Но , т.е. . Из векторной алгебры известно, что площадь треугольника MNP (см.Рисунок 12) Ответ: .

П

Рисунок 13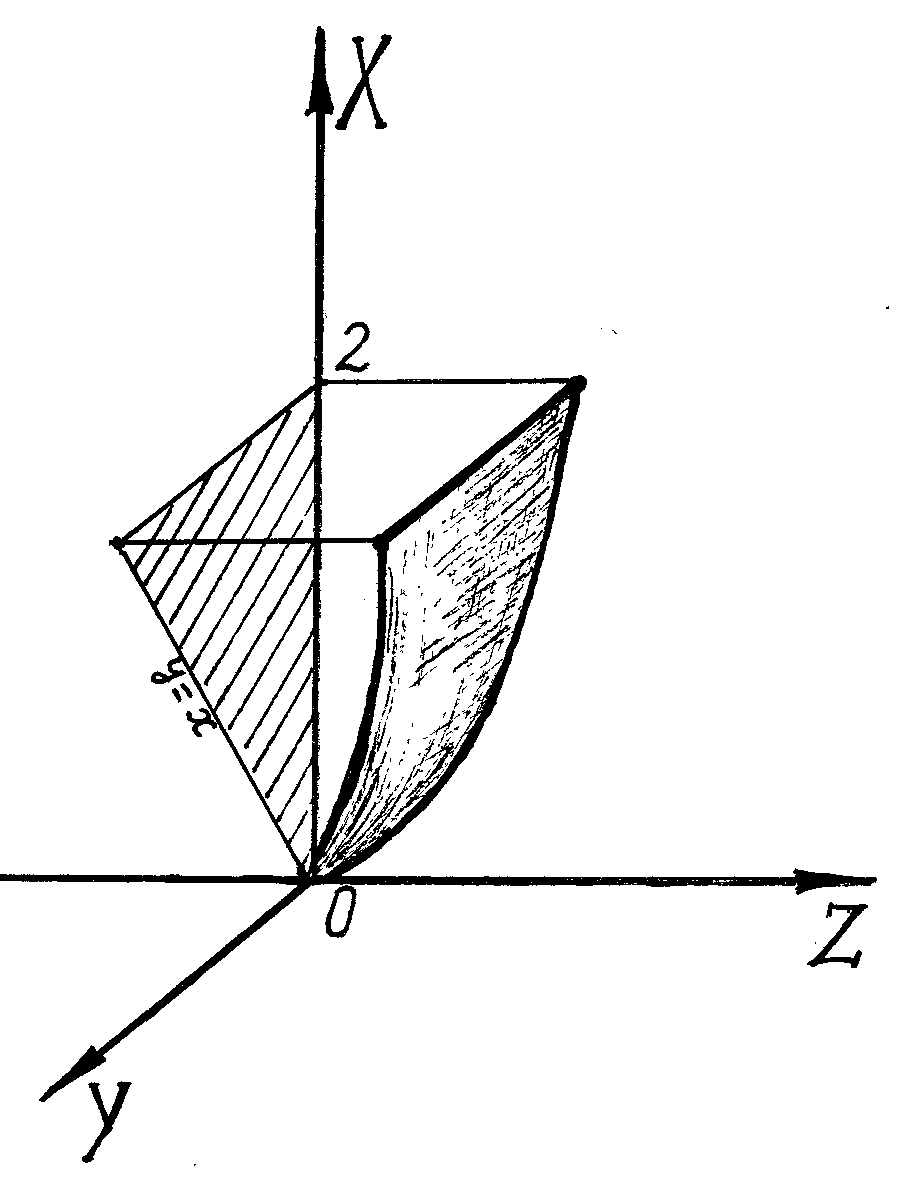

ример 17. Найти поток векторного поля через часть поверхности , если вектор нормали к поверхности составляет острый угол с положительным направлением оси OX.

Решение. Составим интеграл для вычисления потока поля:

(см. (16)).

По рисунку 12 видим, что вектор составляет с OX острый угол, с OY - прямой, с OZ – тупой, следовательно, .

Из (18) следует: .

Вычислим . Проекция линии пересечения и на плоскость YOZ: . Тогда: .Из уравнения поверхности . Тогда

.

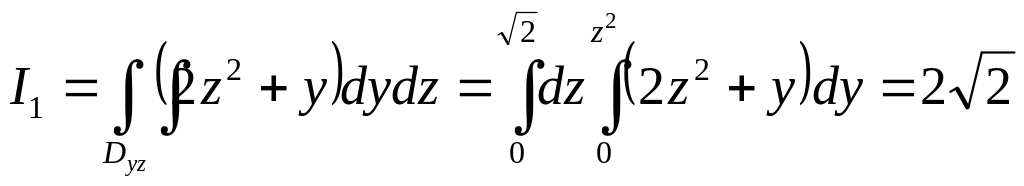Вычислим . Из уравнения поверхности . Тогда

.

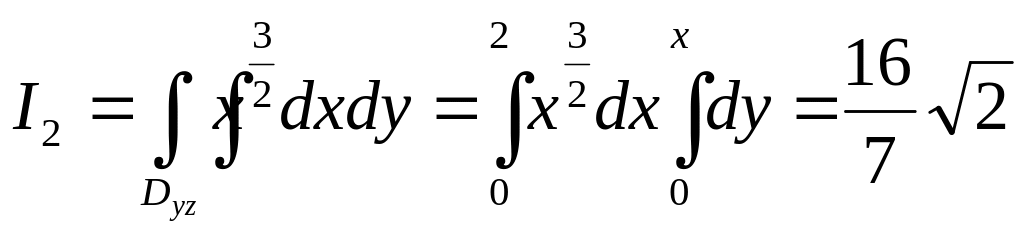Получаем поток .

Результат можно проверить, сведя задачу к поверхностному интегралу I рода. Для этого найдём направляющие косинусы и вычислим . Если уравнение поверхности имеет вид , то вектор нормали к ней , а .

В примере (15) уравнение поверхности: . Учитывая, что нормальный вектор составляет острый угол с осью OX, имеем . Тогда .

Для вычисления этого интеграла I рода спроектируем σ на плоскость XOY (см. рис. 12), тогда:

Из уравнения поверхности : , .

Получаем .

Ответ: .