Контрольное задание 4.

Найти векторные линии поля:

1) ; 2) ; 3) ; 4) .

§6. Линейный интеграл векторного поля.

Линейный интеграл векторного поля – это криволинейный интеграл второго рода. Вводится он следующим образом. Пусть в области G задано векторное поле , и в этом поле определена гладкая или кусочно-гладкая ориентированная кривая АВ. Разобьём кривую АВ на n частей точками деления по направлению от А к В. Радиус-вектор точки обозначим . Вектор . Выберем произвольно на каждой частичной дуге точку и вычислим значение поля в них. Для всех вычислим значения скалярного произведения и составим сумму вида .

Определение 6. Линейным интегралом векторного поля вдоль дуги АВ называется предел (если он существует), к которому стремится интегральная сумма , если наибольшая из длин частичных дуг стремится к нулю, а число элементарных дуг n неограниченно возрастает. Этот предел обозначают символом . Т.е.

. (5)

При изменении ориентации кривой интеграл меняет знак: .

Физический смысл выражения - это работа, произведённая силой при перемещении материальной точки от А к В по контуру L.

Линейный интеграл векторного поля вдоль замкнутой кривой (контура L) называется циркуляцией поля по замкнутому контуру при заданном направлении обхода контура и обозначается символом

Ц (6)

(знак + обозначает, что контур обходится против часовой стрелки).

Пусть поле задано своими функциями-координатами: и . Тогда

. (7)

В правой части выражения (7) - криволинейный интеграл второго рода.

Для плоского поля линейный интеграл вычисляется по формуле: . (8)

Линейный интеграл векторного поля вычисляется по обычным правилам вычисления криволинейного интеграла второго рода, т.е. преобразовывается в определённый. Для этого все переменные под знаком интеграла выражают через одну переменную, используя уравнение той линии, вдоль которой производится интегрирование.

Если векторное поле задано в пространстве , а линия АВ задана параметрическими уравнениями то

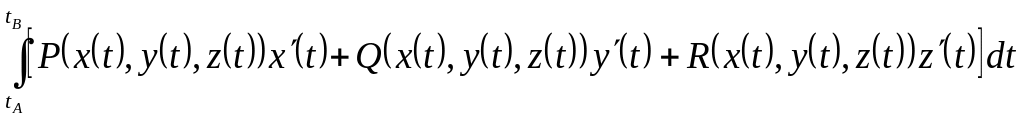. (7.1)

Если линия АВ задана системой уравнений то

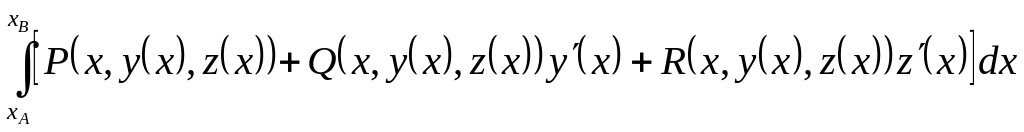. (7.2)

Для плоского векторного поля и линии АВ, заданной параметрическими уравнениями , криволинейный интеграл вычисляется по формуле:

, (8.1)

где - значения параметра t, соответствующие начальной и конечной точкам пути интегрирования.

Для дуги АВ, заданной уравнением : 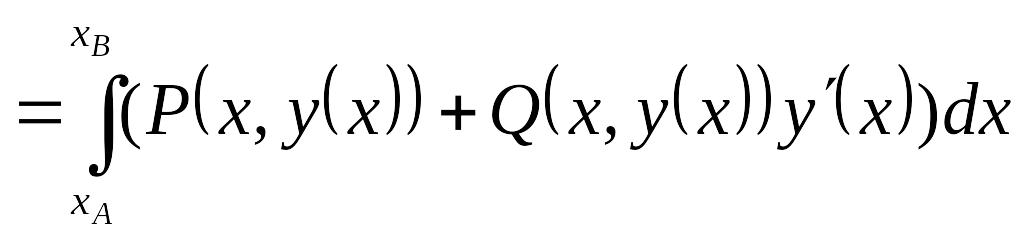. (8.2)

Если линия АВ кусочно-гладкая, то следует воспользоваться свойством аддитивности криволинейного интеграла, разбив АВ на гладкие дуги.

Пример 10. Найти работу векторного поля при перемещении точки вдоль контура, состоящего из части кривой от точки до и дуги эллипса от точки до .

Р

Рисунок 6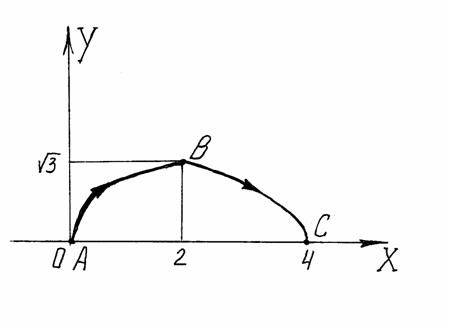

ешение.

Работа (см. (8)).

Т. к. контур состоит из двух частей, воспользуемся свойством аддитивности криволинейного интеграла: . Сведём оба интеграла к определённым по формулам (8.1) и (8.2).

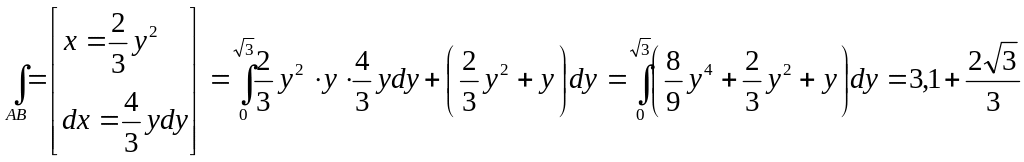
Для вычисления интеграла по контуру ВС используем параметрическую форму записи уравнения эллипса.

.

Ответ: .

Пример 11. Вычислить циркуляцию векторного поля вдоль части кривой Вивиани, заданной пересечением полусферы и цилиндра , пробегаемой против часовой стрелки, если смотреть с положительной части оси OX.

Решение.

Рисунок 7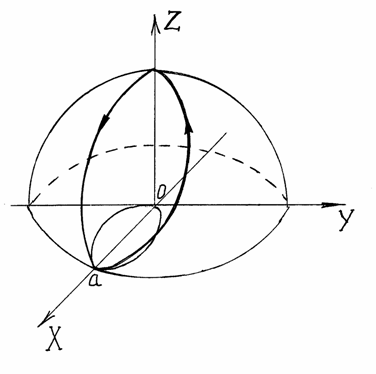

Воспользуемся формулой (7). Ц .

Чтобы свести подынтегральное выражение к одной переменной, перейдём в цилиндрическую систему координат: . Т.к. точка перемещается по кривой , то считаем параметром полярный угол , , и получаем следующие параметрические уравнения этой кривой:

. Тогда .

Подставим полученные выражения в формулу для вычисления циркуляции:

Ц .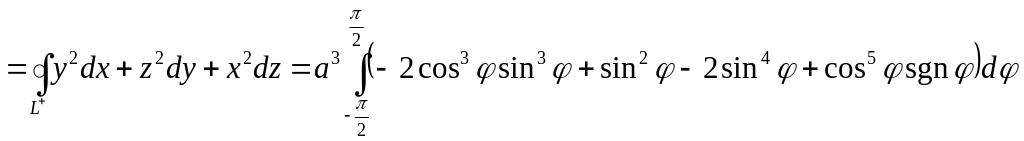

Учитывая свойства интегралов по симметричному интервалу от нечётных и чётных функций, получим: , и

Ц .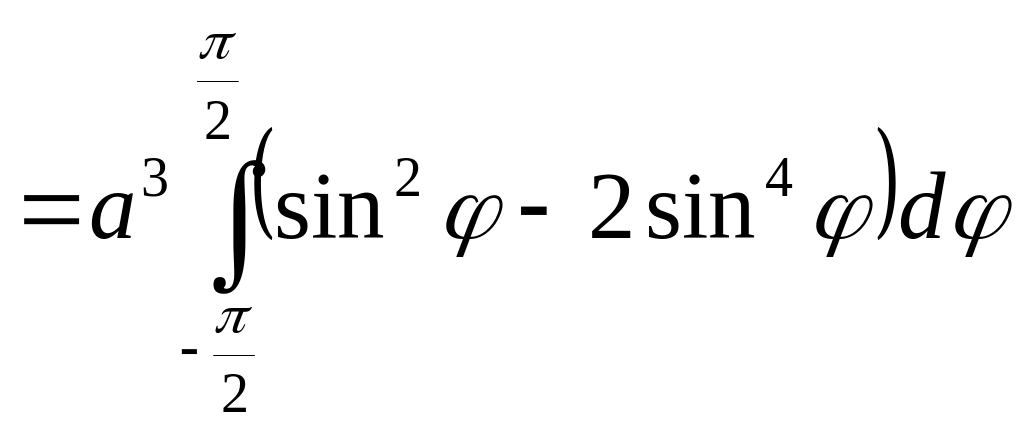

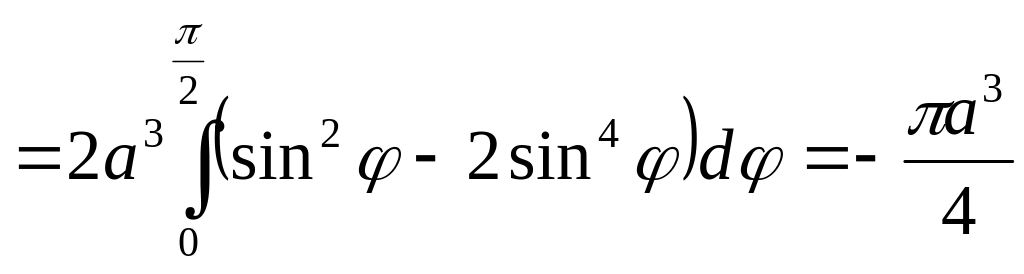Ответ: Ц= .