Формула Грина.

Для плоского векторного поля имеет место следующее утверждение.

Если функции и их частные производные непрерывны в замкнутой области Г, где Г – граница односвязной области G, то

- формула Грина. (10)

обозначает положительное направление обхода (против часовой стрелки).

Пример 12. Используя формулу Грина, вычислить циркуляцию векторного поля по контуру, состоящему из отрезков OA, OB и большей дуги окружности , соединяющей точки A и B, если , , .

Р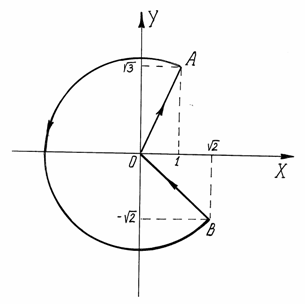 ешение.

Рисунок 8

По формуле Грина: Ц . , ; , . Ц .

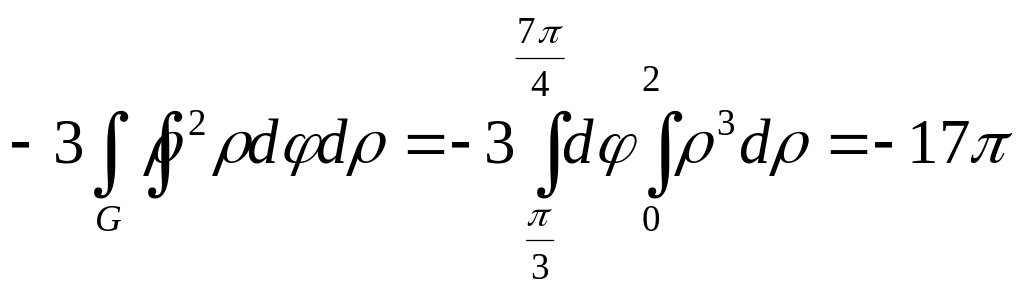Проверим ответ, вычислив циркуляцию непосредственно по контуру с помощью линейного интеграла: Ц .

.

.

.

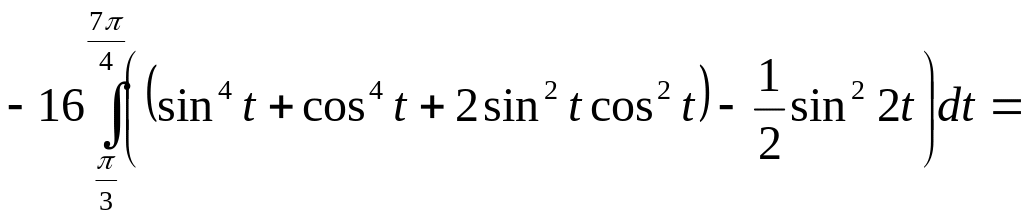
Ответ: Ц .

Контрольное задание 5.

Вычислить линейные интегралы векторного поля:

1) по ломаной .

2) по эллипсу а) , б) .

3) Вычислить циркуляцию векторного поля вдоль эллипса, полученного от пересечения цилиндра плоскостью в направлении по часовой стрелке, если смотреть из точки (0;10;0).

4) Вычислить линейный интеграл векторного поля вдоль ломаной линии ABOC, где , , , .

5) Найти работу поля вдоль части линии пересечения цилиндров и от точки через до точки .

§7. Потенциальное векторное поле.

Определение 7. Векторное поле называется потенциальным в области G, если существует такая скалярная функция , что её градиент равен : .

Функция называется скалярным потенциалом векторного поля . Если , то из определения (6) следует, что

Пусть функции имеют непрерывные частные производные в односвязной области G. Тогда для потенциального поля можно доказать эквивалентность следующих утверждений:

1) Имеют место равенства: (11)

Для плоского поля: . (11.1)

Это необходимые и достаточные условия потенциальности поля.

2) Циркуляция векторного поля по любому замкнутому контуру равна нулю.

3) В области существует скалярная функция , полный дифференциал которой совпадает с подынтегральным выражением линейного интеграла, т. е. В этом случае функция определяется не однозначно, а с точностью до постоянного слагаемого, т.к.

4) Криволинейный интеграл потенциального векторного поля не зависит от пути, соединяющего две произвольные точки и , а зависит только от положения этих точек. Имеет место формула Ньютона-Лейбница.

, (12)

т.е. работа в потенциальном поле не зависит от выбора пути между точками А и В, и равна разности потенциалов в этих точках.

Примеры потенциальных полей.

1. Рассмотрим поле тяготения точечной массы m, помещённой в начало координат О(0,0,0). Такое поле описывается вектор-функцией , где γ – гравитационная постоянная, - радиус-вектор точки , . С такой силой действует поле на единичную массу, помещённую в точку . Поле тяготения потенциально. Его можно представить как градиент скалярной функции , называемой ньютоновским потенциалом поля тяготения точечной массы m. В самом деле:

Аналогично: Тогда

2. Поле электрического точечного заряда е, помещённого в начало координат, описывается в точке вектором напряжённости , ( , .) Это поле потенциально. Его можно представить как градиент скалярной функции , которая называется потенциалом электрического поля точечного заряда е. .

Определение 8. Поверхности уровня (линии уровня для плоского поля) потенциала называются эквипотенциальными поверхностями (линиями).

Отметим, что эквипотенциальная поверхность (линия) и векторная линия, проходящие через общую точку , взаимно ортогональны в ней.

Пример 13. Проверить, является ли поле потенциальным. Если является, то найти потенциал поля, построить эквипотенциальные линии и векторные линии поля. Выделить векторную и эквипотенциальную линии, проходящие через точку .

Решение. Поле определено на всей плоскости XOY.

, ;

Проверим, выполняются ли необходимые и достаточные условия потенциальности: , поле потенциально.

1.Для нахождения функции составим систему: .

Из первого уравнения, проинтегрировав его по переменной x, найдём:

.(Роль константы здесь играет любая функция, зависящая от x). Для отыскания подставим найденную функцию во второе уравнение системы:

. Получили .

2.Условие эквипотенциальности: , отсюда получаем семейство эквипотенциальных линий .

Приведём уравнение к каноническому виду:

.

Это семейство гипербол при .

Если , получим уравнения прямых .

Строим эквипотенциальные линии на плоскости XOY.

3 .Векторные линии поля . Составим дифференциальное уравнение векторных линий поля: .Решим его :

Рисунок 9

- семейство гипербол, если , и две прямые , если . Строим векторные линии на плоскости XOY.

Эквипотенциальные и векторные линии в точках пересечения ортогональны. Проверим это для линий, проходящих через точку .

4.Подставим координаты точки в уравнение векторных линий: . Через точку М проходит векторная линия .

Аналогично найдём для эквипотенциальной линии, проходящей через точку М: . Через точку М проходит эквипотенциальная линия .

Вычислим угловые коэффициенты касательных к этим кривым в точке М:

Для векторной линии: в т. М: .

Для эквипотенциальной линии в т. М: .

- условие перпендикулярности двух касательных.

Вывод: векторная и эквипотенциальная линии в точке М ортогональны.

П

Рисунок 10

ример 14. Убедиться, что поле является потенциальным, найти потенциал поля и вычислить работу, совершаемую этим полем при перемещении материальной точки из в .

Решение. Для ответа на вопрос о потенциальности данного поля вычислим частные производные от функций , , . Эти функции непрерывны вместе со своими частными производными в любой точке .

; ; ; ; ; .

Видим, что выполняются необходимые и достаточные условия потенциальности поля : , , , ч. т. д.

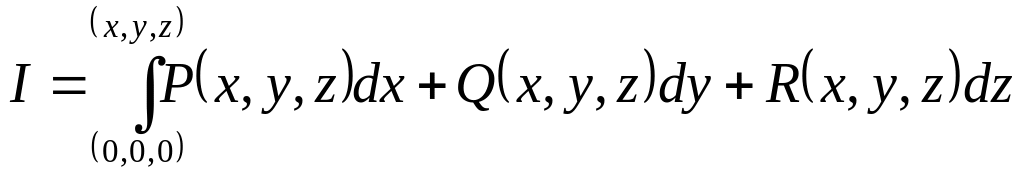
Для вычисления потенциала воспользуемся тем, что линейный интеграл в таком поле не зависит от пути интегрирования и может быть вычислен по формуле Ньютона-Лейбница. Пусть точка - начало пути, а некоторая точка - конец пути. Вычислим интеграл 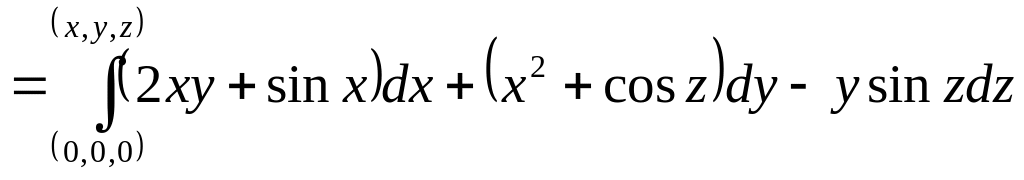по контуру, состоящему из отрезков прямых, параллельных координатным осям (см.Рисунок 10). .

Уравнения частей контура: , , .

Тогда

, x здесь зафиксирован, поэтому ,

, здесь зафиксирован y, поэтому .

В итоге получаем: .

Теперь тот же интеграл вычислим по формуле Ньютона-Лейбница. = = .

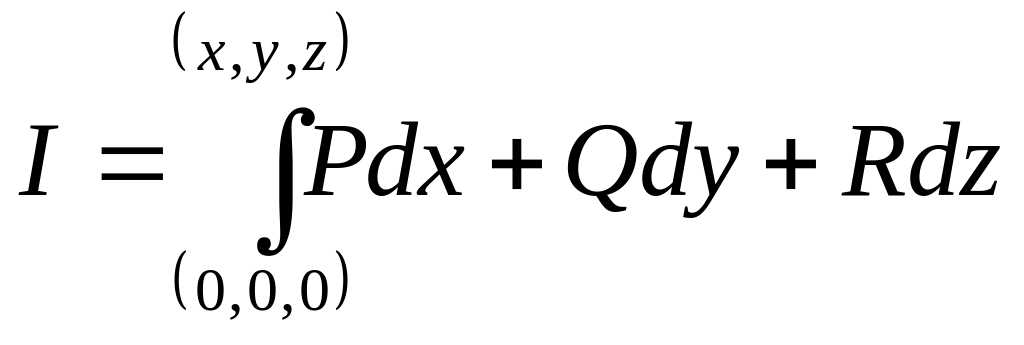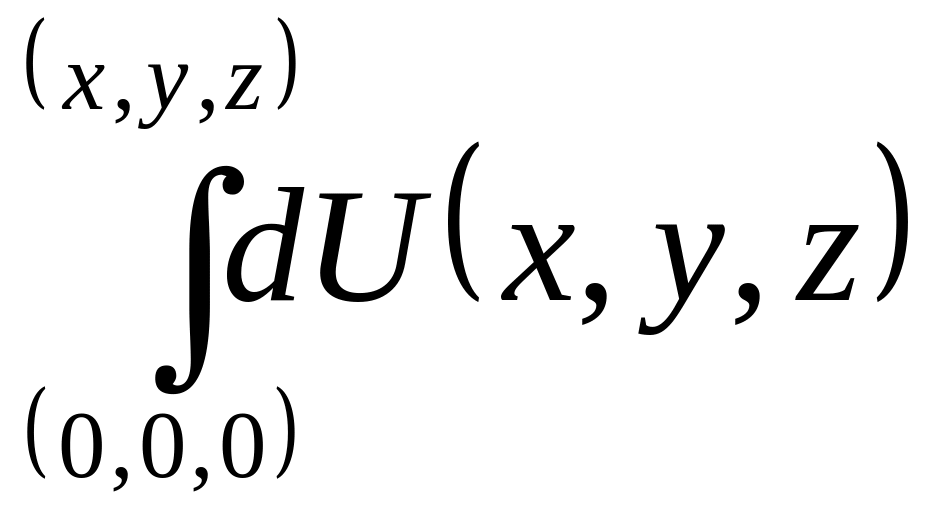Приравняем результаты: .

Из полученного равенства следует, что , а Потенциал данного поля найден.

Найдём работу, совершаемую векторным полем при перемещении точки из в . В потенциальном поле работа равна разности потенциалов в конечной и начальной точках пути, т. е.

Пример 15. Убедиться в потенциальности векторного поля , найти уравнения эквипотенциальных поверхностей и выделить среди них ту, которая проходит через точку M(2,1,1).

Решение. Поле определено в каждой точка пространства . Проверим потенциальность поля (см. (11)):

условия выполнены, поле потенциально. Можно найти потенциал так же, как в примере 12, а можно другим способом. Для нахождения потенциала имеем систему:

.

Интегрируя первое уравнение системы по переменной x, найдём . Продифференцируем полученное выражение по y: .Из второго уравнения системы получаем: .Уточним выражение для потенциала:

. Дифференцируем по переменной z и сравниваем с третьим уравнением системы: .

Восстановим всю функцию: . Потенциал найден.

Потребовав , получим уравнения эквипотенциальных поверхностей:

.

Приведём это уравнение к каноническому виду: .

Это уравнения сфер с центром в точке O(0;1;1) и радиусом

Найдём эквипотенциальную поверхность, проходящую через точку M(2,1,1). Подставим координаты точки в уравнение поверхности, определим :

через точку М проходит сфера .

Найдём векторную линию поля, проходящую через точку М.

Уравнения векторных линий:

Рисунок 11

в т. М: , т. е. через т. М проходит прямая . Т.к. она проходит через центр сферы, касательная плоскость к сфере в т. М ей перпендикулярна. Т. е. векторная линия и эквипотенциальная поверхность в т. М взаимно ортогональны.

Направление движения поля по этой линии совпадает с направлением оси OX при x>0 и противоположно ему при x<0. Это совпадает с направлением увеличения потенциала U. Действительно, чем больше потенциал, тем больше радиус сферы.