
- •§1. Скалярные и векторные поля.
- •§2. Поверхности и линии уровня.
- •§3. Производная по направлению скалярного поля.
- •Контрольное задание 2.
- •§4. Градиент скалярного поля.
- •Контрольное задание 3.
- •§5. Векторные линии поля.
- •Контрольное задание 4.
- •§6. Линейный интеграл векторного поля.
- •Формула Грина.
- •Контрольное задание 5.
- •§7. Потенциальное векторное поле.
- •Примеры потенциальных полей.
- •Контрольное задание 6.
- •§8. Поток векторного поля.
- •Контрольное задание 7.
- •§9. Дивергенция векторного поля. Соленоидальное векторное поле.
- •Формула Остроградского – Гаусса.
- •Контрольное задание 8.
- •§10. Ротор (вихрь) векторного поля. Формула Стокса.
- •Контрольное задание 9.
- •§11. Операторы Гамильтона и Лапласа.
- •Дифференциальные операции второго порядка.
- •Запись дифференциальных операций второго порядка в операторной форме.
- •Контрольное задание 10.
- •Ответы к контрольным заданиям.
- •Список литературы.
- •Оглавление.
- •Скалярные и векторные поля. 4
§3. Производная по направлению скалярного поля.
Пусть
-
скалярное поле, заданное в области
![]() .
.
![]() - единичный фиксированный вектор. М
– фиксированная
точка,
- единичный фиксированный вектор. М
– фиксированная
точка,
![]() .
.
![]() -
произвольная, отличная от М,
точка из G,
такая, что
вектор
-
произвольная, отличная от М,
точка из G,
такая, что
вектор
![]() коллинеарен
.
Пусть
коллинеарен
.
Пусть
![]() -
величина направленного отрезка
(равная
-
величина направленного отрезка
(равная
![]() ,
если
,
если
![]() и равная -
и равная -![]() ,
если
,
если
![]() ).
).
Определение 2.
Число
![]() называется производной скалярного
поля в направлении
в
точке М и
обозначается символом
называется производной скалярного
поля в направлении
в
точке М и
обозначается символом
![]() .
.
Производная
скалярного поля в направлении
в точке М
равна скорости
изменения поля в этой точке в данном
направлении. Если
![]() ,
то при перемещении из точки М
в направлении
значение поля (функция
,
то при перемещении из точки М
в направлении
значение поля (функция
![]() )
возрастает, если
)
возрастает, если
![]() - убывает.
- убывает.
Пусть поле
задано в декартовой системе координат
и
![]() -
единичный вектор данного направления.
Тогда производная скалярного поля в
направлении
в точке M
вычисляется
по формуле:
=
-
единичный вектор данного направления.
Тогда производная скалярного поля в
направлении
в точке M
вычисляется
по формуле:
=![]() +
+![]()
![]() ,где α,β,γ – углы, образуемые вектором
с соответствующими осями координат и
,где α,β,γ – углы, образуемые вектором
с соответствующими осями координат и
![]() .
.
Если
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() ,
,
Для плоского поля
![]() производная по направлению вычисляется
по формуле:
=
производная по направлению вычисляется
по формуле:
=![]() +
+![]() =
+
=
+![]() .
.
Пример 3. Установить
характер изменения поля, заданного
функцией
![]() в точке
в точке
![]() в направлении от А
к точке
в направлении от А
к точке
![]() .
.
Решение.
![]()
![]() ,
,
![]() ,
,
![]() .
.
Значения производных
в точке А:
![]()
![]()
![]()
![]() =
+
=
+![]()
![]()
Ответ:
Т.к.
![]() поле убывает в направлении
поле убывает в направлении
![]() .
.
Пример 4. Найти
производную функции
![]() в точке
в точке
![]() в направлении, составляющем угол
в направлении, составляющем угол
![]() с положительным направлением оси ОХ.
с положительным направлением оси ОХ.
Решение.
Для плоского поля
![]() =
=![]() +
+![]() .
.
Значения производных
в точке M:
![]() ,
,
![]() .
.
![]()
![]() Ответ:
Ответ:
![]()
Контрольное задание 2.
Найти производную функции:
1)![]() в точке
в точке
![]() в направлении вектора
в направлении вектора
![]() ,
составляющем угол
с
положительным направлением оси ОХ;
,
составляющем угол
с
положительным направлением оси ОХ;
2)
![]() в точке
в точке
![]() в направлении вектора
в направлении вектора![]() ,
где
,
где
![]() ;
;
3)
![]() в точке
в точке
![]() в направлении вектора
в направлении вектора
![]() ;
;
§4. Градиент скалярного поля.
Определение 3.
Градиентом
скалярного поля
называется вектор-функция
![]() ,
(1)
,
(1)
координатами которой являются соответствующие частные производные данной функции.
Если
![]() -
единичный вектор данного направления,
то из формулы (1) следует, что производная
по направлению
-
это скалярное произведение векторов
-
единичный вектор данного направления,
то из формулы (1) следует, что производная
по направлению
-
это скалярное произведение векторов
![]() и
,т.е
и
,т.е
![]()
![]()
![]() .
.
Но
=![]()
![]() .
Тогда
.
Тогда
![]() ,
т. к.
,
т. к.
![]() .
.
Здесь
![]() - угол между вектором градиента в данной
точке и вектором
.
- угол между вектором градиента в данной
точке и вектором
.
О
Рисунок 3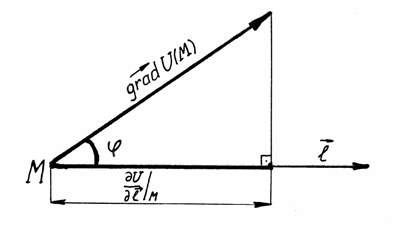
1. Вектор
в данной точке указывает направление
наибольшего роста поля (функции![]() )
в этой точке. При этом
)
в этой точке. При этом
![]()
![]() - наибольшее значение производной по
направлению в точке M.
(Таким образом, вектор
не зависит от выбора системы координат,
а его модуль и направление в каждой
точке определяются функцией
).
- наибольшее значение производной по
направлению в точке M.
(Таким образом, вектор
не зависит от выбора системы координат,
а его модуль и направление в каждой
точке определяются функцией
).
2. Градиент скалярного поля в точке М ортогонален к поверхности (линии) уровня поля, проходящей через точку М.
3. Если
![]() - поле постоянно, то его градиент равен
0.
- поле постоянно, то его градиент равен
0.
4. Справедливы формулы:
а)
![]() ;
б)
;
б)
![]()
в)
![]() ;
г)
;
г)
![]()
д)
![]() ,
где U
и V
– скалярные поля.
,
где U
и V
– скалярные поля.
е)
![]() .
.
Пример 5.
Найти градиент электростатического
поля
![]() ,
где е
- заряд,
,
где е
- заряд,
![]() -
расстояние от данной точки до заряда.
-
расстояние от данной точки до заряда.
Решение. Данному полю принадлежат все точки пространства за исключением начала координат, где U обращается в бесконечность.
По определению: . Вычислим частные производные:
![]()
![]()
![]()
![]() .
.
Ответ:
![]() .
.
Пример 6. Найти
наибольшую скорость возрастания функции
![]() в точке
в точке
![]() .
.
Решение.
Направление наибольшего возрастания
поля указывает вектор градиента этого
поля.
![]() .
.
Вычислим значения
частных производных в точке M:
![]()
![]()
![]()
![]()
Наибольшая скорость
возрастания
равна наибольшему значению производной
по направлению точке M
![]()
Ответ: Наибольшая
скорость возрастания функции
![]()
