8.5. Поверхности в трехмерном евклидовом пространстве

Пусть 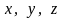– декартовы координаты в трехмерном евклидовом пространстве , – множество точек плоскости .

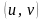Определение 11. Непрерывное отображение 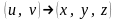множества , где 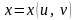, , 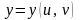, 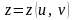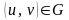(39)

в евклидово пространство называют поверхностью. Здесь – непрерывные функции переменных _.

Три скалярных равенства (39) можно записать в векторной форме

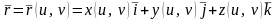, (40)

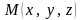где – радиус вектор точки в .

Переменные называются координатами или параметрами на поверхности 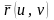. Образ множества при отображении (39) или (40) представляет собой некоторое множество в евклидовом пространстве , которое также называется поверхностью и обозначается 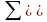. Если возникающее при этом соответствие между множеством и его образом однозначно, то говорят, что поверхность 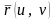не имеет самопересечений.

Пример 15. Два отображения

,

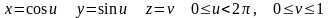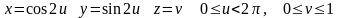
определяют различные поверхности, несмотря на то, что образами множества 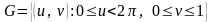в обоих случаях будет одно и тоже множество, а именно: 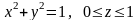. В первом случае поверхность не имеет самопересечений, а во втором имеет самопересечение.

Пусть – область, открытое связанное множество на плоскости .

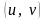Определение 12. Поверхность 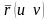называется гладкой, если функции 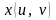, , 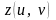имеют непрерывные частные производные первого порядка в области , т.е. непрерывно дифференцируема в .

Определение 13. Гладкая поверхность называется регулярной, если в любой точке 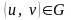ранг матрицы Якоби

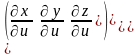
равен двум.

Это означает, что 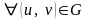векторы 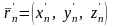и 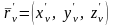линейно независимы, что равносильно тому, что

.

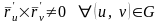Пусть – гладкая регулярная поверхность без самопересечений, заданная уравнением (39) или (40). Ее геометрический образ будет обозначен . Пусть 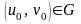– фиксированная точка. Ей соответствует точка , где

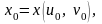
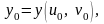
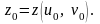
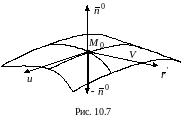
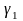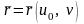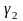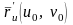Зафиксируем одну из переменных . Тогда векторная функция будет определять гладкую кривую на (рис. 10.7). Вектор-функция будет определять гладкую кривую на . Кривые проходят через точку . Векторы и 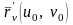будут касательными векторами в точке 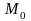к и соответственно. Кривые 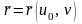и 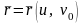называются координатными линиями на .

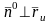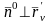Вектор называют нормальным вектором поверхности. Ясно, что и . Обозначим единичный нормальный вектор

.

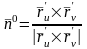Таким образом, в каждой точке гладкой поверхности существует два направления и .

Определение 14. Ориентацией гладкой регулярной поверхности называется непрерывная единичная нормаль. Поверхность, у которой фиксирована ориентация, называется ориентированной. Для гладкой регулярной поверхности без самопересечений есть две нормали – положительная и – отрицательная.

Ориентированную поверхность также называют двухсторонней. Ее можно также определить следующим образом: какова бы не была замкнутая кривая, целиком лежащая на поверхности и не пересекающая границы поверхности, вектор нормали при перемещении вдоль этой кривой по поверхности возвращается в исходное положение.

В противном случае поверхность называется односторонней. Примером неориентированной или односторонней поверхности является лист Мёбиуса (рис. 8.8). При движении по средней линии листа от точки 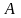единичный вектор нормали непрерывно поворачивается. При возвращении в точку единичный вектор нормали изменит направление на противоположное. Поэтому на этой поверхности нельзя построить непрерывное поле нормали. Лист Мебиуса не ориентируемая поверхность.

Найдем направляющие косинусы нормали, т.е. координаты единичного вектора . Известно, что 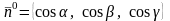и .

1. Поверхность задана параметрически:

.

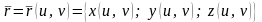Тогда .

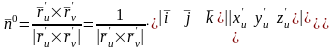Откуда,

,

,

.

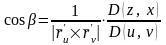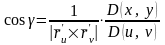2. Поверхность задана в явном виде .

Тогда ее векторное представление , , .

;

.

.

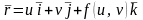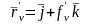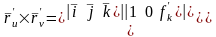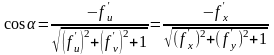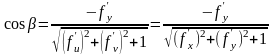. (41)

.

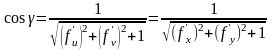Определение 15. Плоскость, проходящая через точку 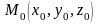поверхности, в которой лежат все касательные к координатным кривым, проходящим через эту точку, называют касательной плоскостью к поверхности в данной точке.

Для гладкой регулярной поверхности 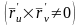в каждой точке есть касательная плоскость, причем единственная.

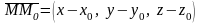П олучим уравнение касательной плоскости в декартовой системе координат с нормалью в точке (рис. 8.9). Пусть произвольная точка, принадлежащая касательной плоскости. Рассмотрим векторы и 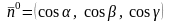. Очевидно, что они ортогональные и их скалярное произведение равно нулю, т. е.

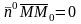, или, записывая скалярное произведение в координатах, получим уравнение касательной плоскости:

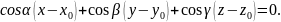
Подставляя значения направляющих косинусов, получим

.

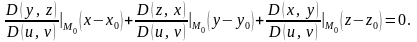Если поверхность задана в явном виде, т.е. , то направляющие косинусы определяются по формулам (41) и уравнения касательной плоскости будет

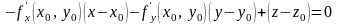
или

.

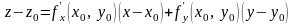Для поверхности заданной неявно уравнением ,

где 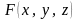непрерывно дифференцируемая функция в окрестности точк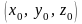и и 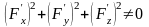уравнение касательной имеет вид

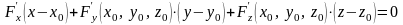, так как нормальным вектором поверхности является grad F(M₀)

Определение 16. Прямая, проходящая через точку касания поверхности с касательной плоскостью и перпендикулярная этой плоскости, называется нормальной прямой (нормалью) к поверхности в этой точке.

Каноническое уравнение прямой в пространстве имеет вид:

,

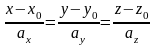Если в качестве направляющего вектора выбран вектор , то уравнение нормали в зависимости от способа задания поверхности будут

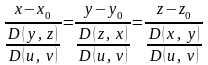
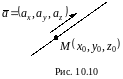
или

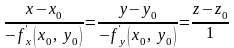
или

.

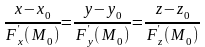Пример 16. Написать уравнения касательной, плоскости, нормальной прямой к сфере x²+y²+z²=4 в точке, проекция которой на плоскость oxy есть точка (1; 1).