8.2. Векторные отображения

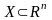Пусть точка множества и пусть на 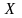заданы следующие функции n-переменных:

, (11)

Таким образом, для каждого фиксированного 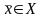можно рассматривать вектор 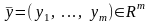. В этом случае говорят, что имеет место векторное отображение 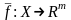или векторная функция .

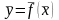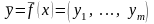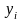У векторной функции , каждая координата является функцией n-переменных . Функции называют координатными функциями отображения 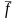, где записывают так .

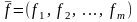Если 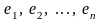– координатные векторы в , а – координатные векторы в 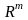, т.е.

, , …, ;

, , …, .

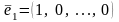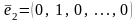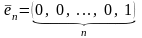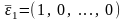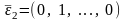Тогда

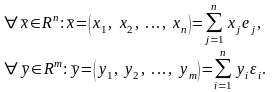
Если 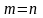, то пространства и можно считать совпадающими и функцию 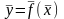можно интерпретировать как отображение в . Такое отображение часто называют векторным полем заданным на . Важным классом векторных отображений 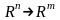являются линейные отображения или линейные векторные функции.

Определение 1. Векторное отображение 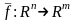называют линейным есл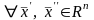и и 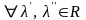, выполняется:

.

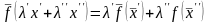Из определения следует, что при линейном отображении любая линейная комбинация векто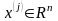ров отображается в такую же линейную комбинацию образов этих векторов

.

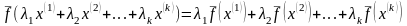Линейные отображения называют также линейными операторами.

Пусть 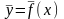линейная векторная функция (линейное отображение или линейный оператор). Образ каждого координатного вектора 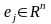, 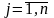при отображении является вектором (точкой) в и поэтому раскладывается по координатным векторам . Обозначим коэффициенты этого разложения через 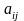, тогда

.

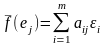Пусть , тогда 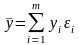. В силу линейности отображения получим (12):

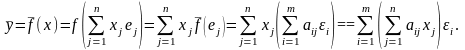
Следовательно, 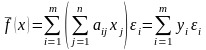. Тогда коэффициенты разложения вектора будут равны коэффициентам при единичных векторах 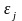, т.е.

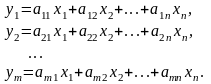(13)

Наоборот, легко проверить, что всякое отображение , координаты которого имеют вид (13), является линейным оператором.

Определение 2. Матрица в (13) называется матрицей линейного оператора .

Очевидно, что если 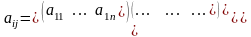есть матрица линейного оператора , то для произвольного вектора 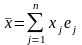имеет место разложение

.

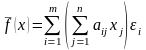Если 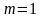, т.е. линейный оператор 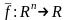отображает во множество действительных чисел, то он обычно называется линейным функционалом или линейной функцией n-переменных.

В силу (13) это будет означать, что

.

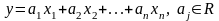Если обозначить 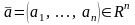, то всякий функционал имеет вид

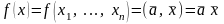– скалярное произведение.

Пример 4. Является ли отображение 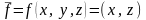линейным.

Решение.

.

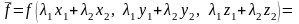
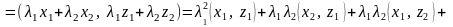
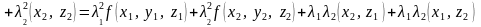Следовательно, по определению 3 отображение не является линейным. 

Пример 5. Является ли отображение 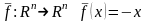линейным.

Решение.

.

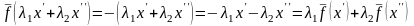Следовательно, отображение является линейным. 

Пример 6. Является ли отображение 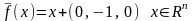линейным.

Решение. . 

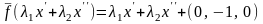Следовательно, по определению 3 отображение не является линейным.

Пример 7. Является ли отображение 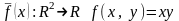линейным.

Решение.

.

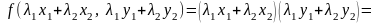
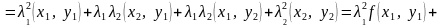
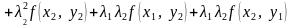Следовательно, отображение не является линейным. 

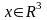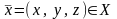В физических приложениях важным является следующий частный случай векторных отображений. Пусть , т.е. и 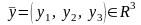. Рассмотрим отображение 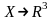, т.е. векторное поле

,

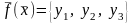где 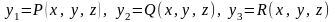– три скалярных функции трех переменных или 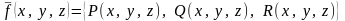. Таким образом, каждой точке трехмерного геометрического пространства ставится в соответствие вектор этого же пространства. Примерами физических векторных полей являются:

• поле гравитации;

• электрическое поле ;

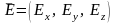• магнитное поле

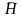
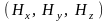
• поле скорости жидкости .

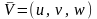Пусть 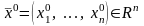и является предельной точкой множества , а . Отображение 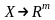задано функцией 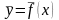. Введем расстояние в

.

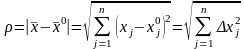Расстояние в пространстве задано следующим образом:

.

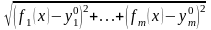Определение 3. Вектор 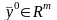называют пределом отображения при , если для любого положительного найдется такое неотрицательное число , что из выполнения условия 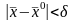будет следовать выполнение неравенства 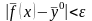, т.е. .
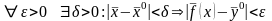