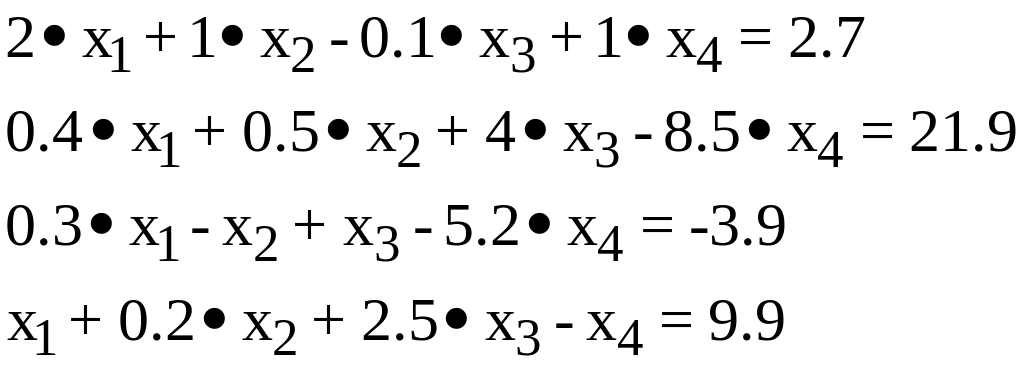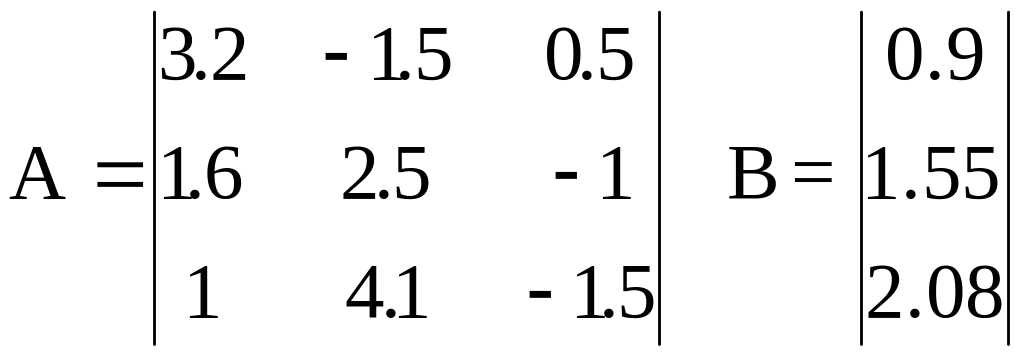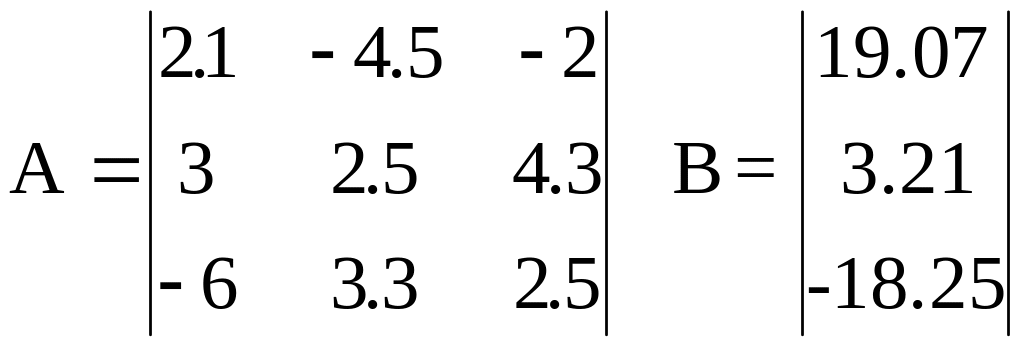ЛАБОРАТОРНАЯ РАБОТА №1
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Цель работы: изучить метод Гаусса, используемый наиболее часто для решения систем линейных алгебраических (СЛАУ) уравнений, разработать алгоритм и на его основе написать программу.
ПРОГРАММА РАБОТЫ
Составить программу решения СЛАУ методом Гаусса.
Запустить программу, решив с её помощью одну из линейных систем
уравнений, в соответствии с вариантом задания.
3. Проверить полученное решение.
4. Оформить отчет о лабораторной работе.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РАБОТЕ
Метод Гаусса. Схема единственного деления
Рассмотрим систему из 4-уравнений с четырьмя неизвестными:
(1)
пусть
(разрешающий элемент)
Разделив первое
уравнение системы (1) на
,
получим
(2)
где
(j=2,3,4,5).
Исключим
из второго, третьего и четвертого
уравнений системы. Для этого умножим
уравнение (2) на
,
и
и вычтем результаты соответственно из
второго, третьего и четвертого уравнений
системы.
В результате получим систему 3 уравнений:
(3)
где
(i=2,3,4; j=2,3,4,5)
Далее первое
уравнение системы (3) делим на
,
в итоге :
, (4)
где
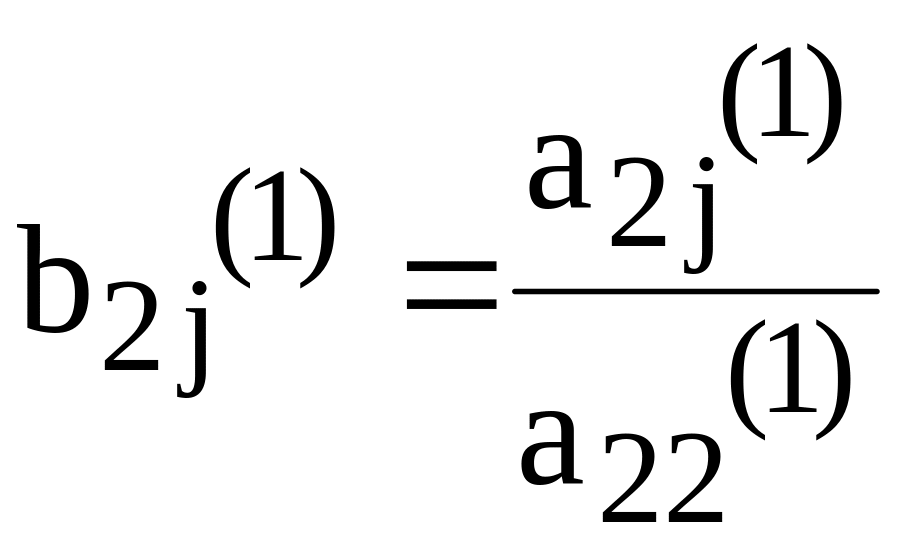(j=3,4,5).
Исключая теперь
так же, как исключили
,
получим систему уравнений
(5)
где
(i=3,4; j=3,4,5).
Разделив первое
уравнение системы (5) на
,
получим
,
где
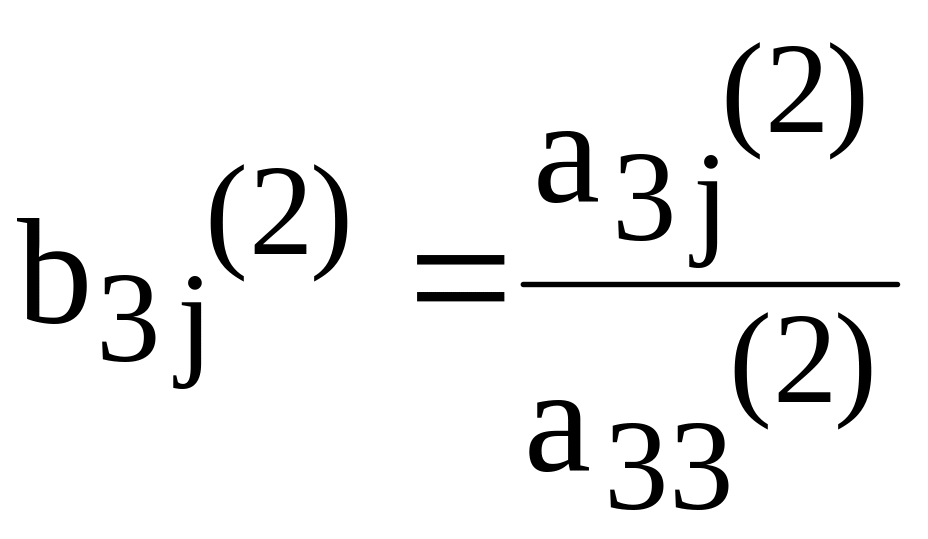(j=4,5).
C помощью этого
уравнения исключим
из второго уравнения системы (5). Получим
уравнение
,
где
(j=4,5).
Таким образом, система (1) приводится к эквивалентной схеме с треугольной матрицей:
(6)
откуда последовательно находятся
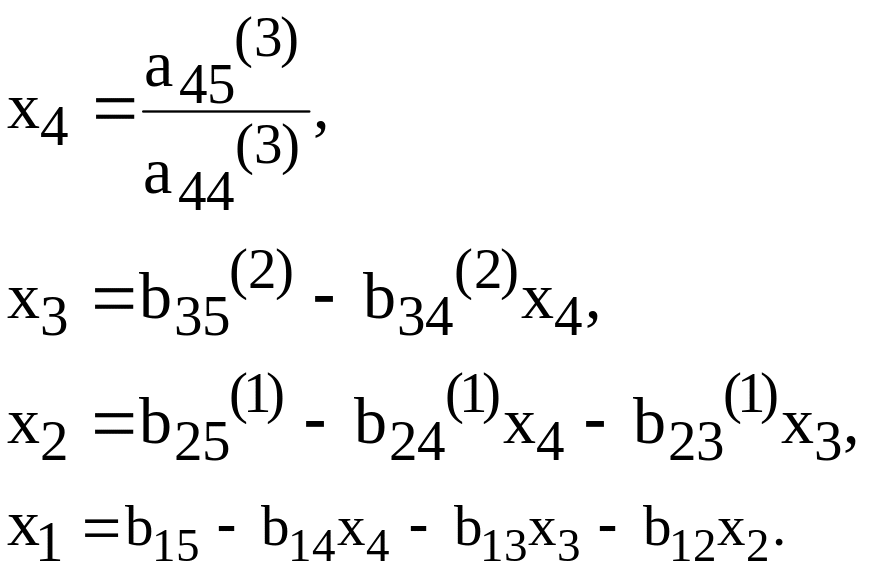(7)
Итак, решение системы распадается на два этапа прямой ход — приведение системы (1) к треугольному виду (6), обратный ход — определение неизвестных по формулам (7).
Рассмотренный метод применим, если все ведущие — разрешающие элементы отличны от нуля. Если же какой-либо из них обращается в ноль, то в соответствующей системе достаточно провести перестановку уравнений, чтобы сделать “ведущий” элемент отличным от нуля. Блок-схема алгоритма (схема единственного деления) приведена на рис.1.
ВАРИАНТЫ ЗАДАНИЙ
А. Решаемые системы уравнений
Решить следующие СЛАУ
1. |
2.
|
3.
|
4.
|
В. Используемые методы
Описанный метод Гаусса (схема единственного деления), с вычислением определителя системы и проверкой на ноль диагонального элемента.
Метод Гаусса с выбором главного элемента.
Метод прямоугольника с расположением разрешающих элементов в любом месте.
Метод квадратных корней с вычислением определителя.
Метод Гаусса для вычисления элементов обратной матрицы.
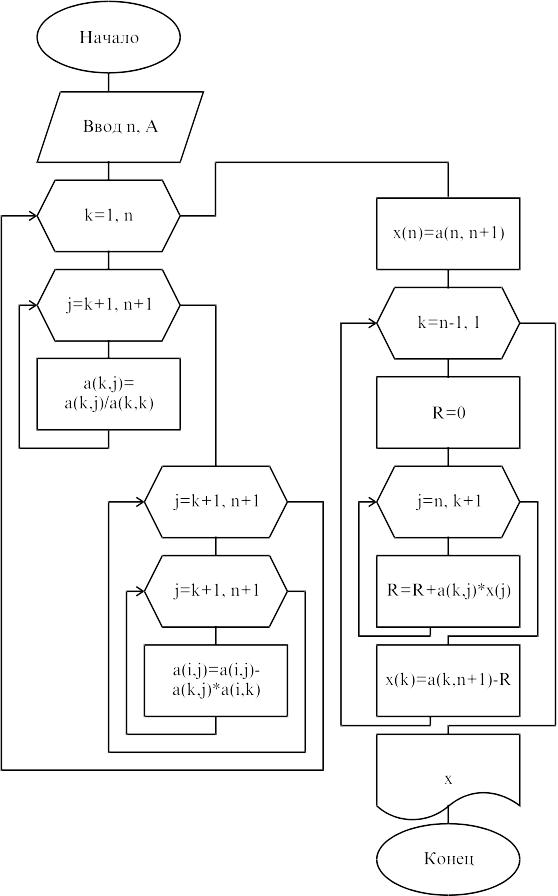Рис.
1. Блок-схема алгоритма
ЛАБОРАТОРНАЯ РАБОТА №2
ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ
Цель работы: изучить итерационные методы, используемые наиболее часто для решения систем линейных алгебраических уравнений, научиться разрабатывать алгоритмы и писать программы на их основе.
ПРОГРАММА РАБОТЫ
Разработать алгоритмы и составить программы решения СЛАУ методом простой итерации и методом Зейделя.
Запустить поочередно обе программы, решив с их помощью одну из линейных систем уравнений, взятую из соответствующего варианта задания.
Произвести сравнительные оценки сходимостей рассматриваемых методов.
Сравнить полученные результаты решения СЛАУ двумя итерационными методами с решением задачи прямым методом.
Исследовать влияние параметров ЭВМ на скорость сходимости итераций.
Оформить отчет о лабораторной работе.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РАБОТЕ
Системы линейных уравнений можно решать не только прямыми, но и итерационными методами. Итерационные методы применяются, главным образом, для решения задач большой размерности, когда использование прямых методов невозможно из-за необходимости выполнения чрезмерно большого числа арифметических операций. Как правило, большие системы уравнений являются разреженными. Применение методов исключения переменных для них бывает неудобным ввиду того, что при их использовании большое число нулевых элементов превращается в ненулевые, и матрица теряет свойство разреженности, чего не происходит при использовании итерационных методов.
Рассмотрим наиболее простые итерационные методы, позволяющие решать достаточно широкий класс систем.