- •Глава 12. Несобственные интегралы и интегралы, зависящие от параметра
- •12.1. Несобственные интегралы с бесконечными пределами интегрирования.
- •Интегралы, зависящие от параметра
- •9.5.1. Собственные интегралы, зависящие от параметра. Рассмотрим следующий интеграл:
- •9.6.2. Несобственные интегралы, зависящие от параметра. Пусть функция определена на множестве . Будем рассматривать интегралы вида:
Глава 12. Несобственные интегралы и интегралы, зависящие от параметра
12.1. Несобственные интегралы с бесконечными пределами интегрирования.
Определение
5 . Пусть
функция
![]() определена
на промежутке
определена
на промежутке
![]() и интегрируема по Риману на любом отрезке
и интегрируема по Риману на любом отрезке
![]() .Если
существует (конечный) предел
.Если
существует (конечный) предел
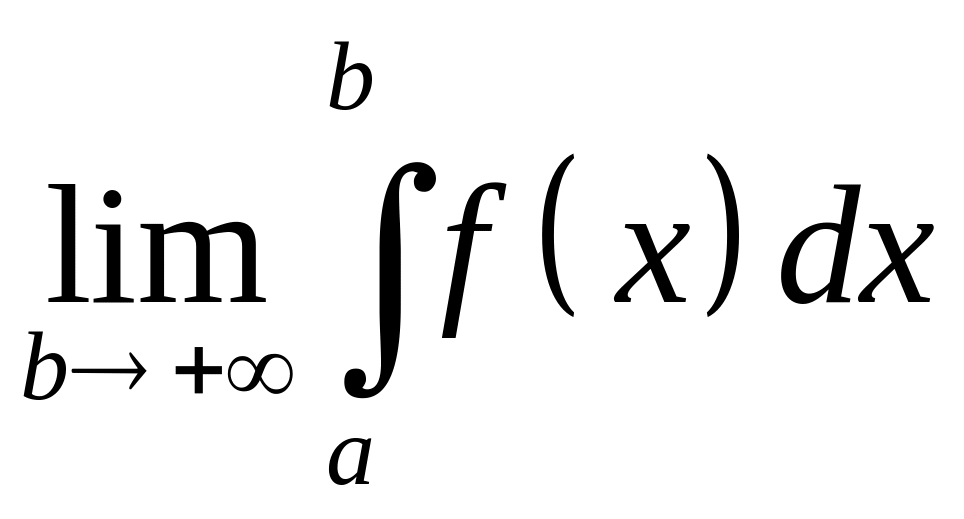 ,
,
то его называют несобственным интегралом и обозначают
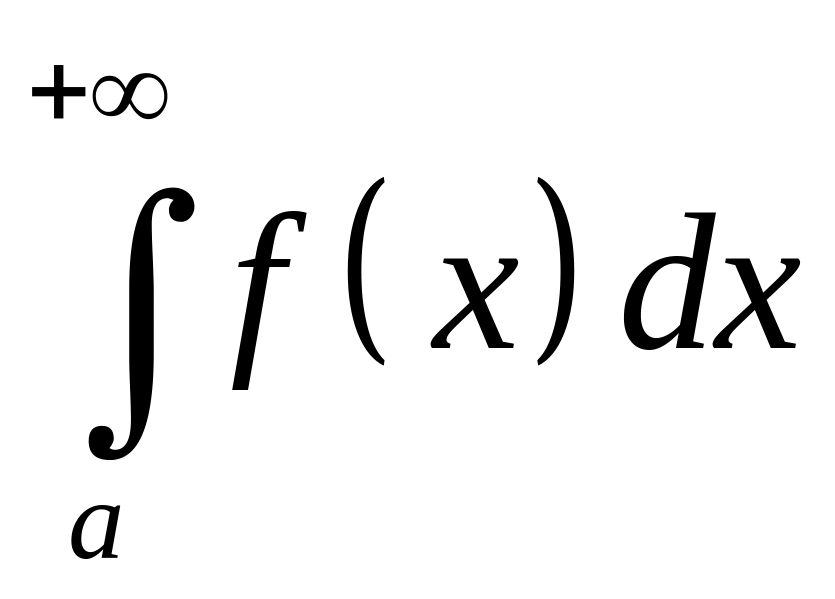 .
.
Таким образом
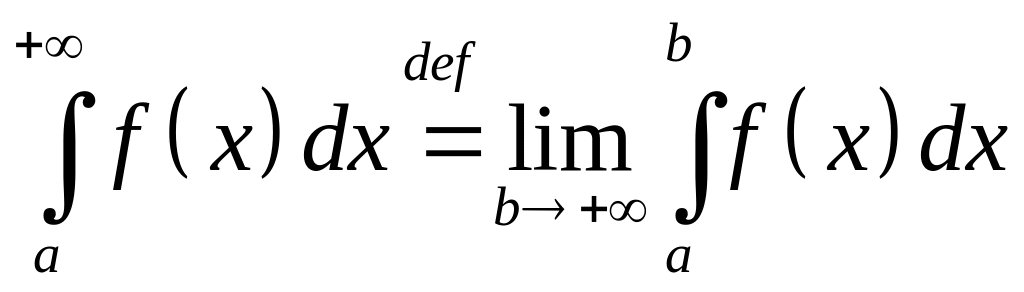 (30)
(30)
В этом случае говорят также, что несобственный интеграл (30) сходится на промежутке , а функция называется интегрируемой (в несобственном смысле) на промежутке . Если же предел не существует, то говорят, что интеграл расходится.
Замечание
1. Если
![]() ,
то интегралы
и
,
то интегралы
и
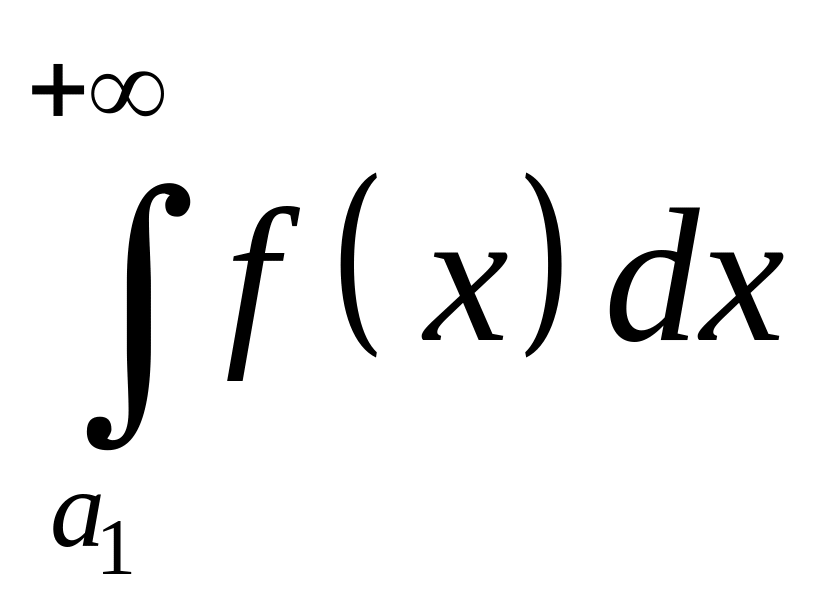 сходятся или расходятся одновременно,
т.к.
сходятся или расходятся одновременно,
т.к.
 то
и
то
и
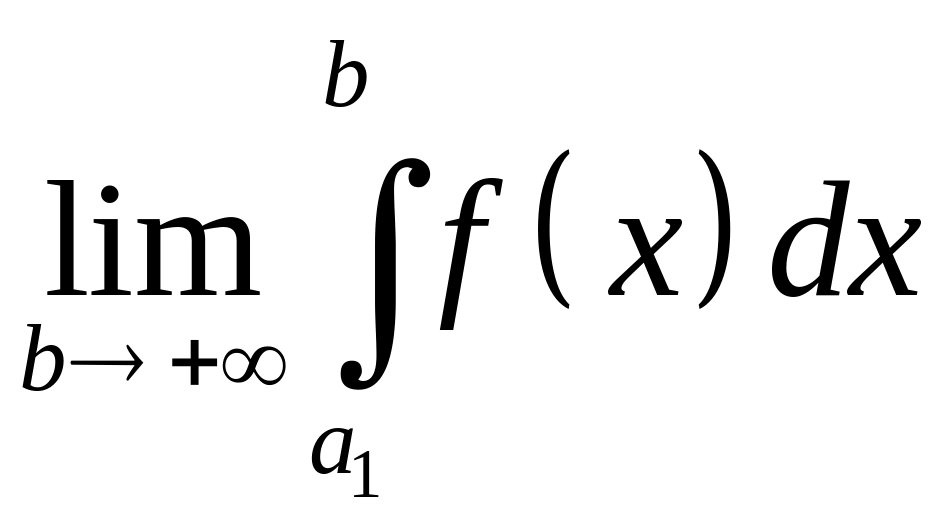 существуют одновременно.
существуют одновременно.
Замечание
2. Если
имеет первообразную
![]() на промежутке
,
то
на промежутке
,
то

Замечание 3. Очевидно, что выполняется свойство линейности
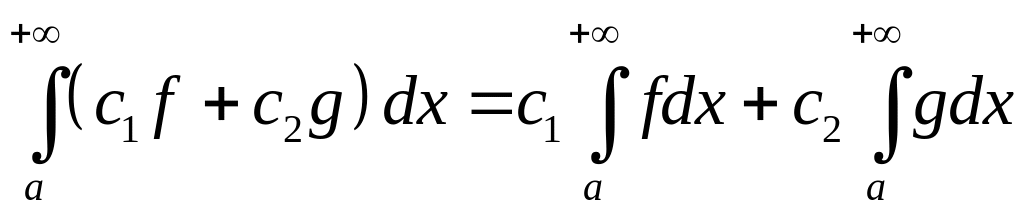 ,
если интегралы
и
,
если интегралы
и
![]() существуют.
существуют.
Аналогично
определяются несобственные интегралы
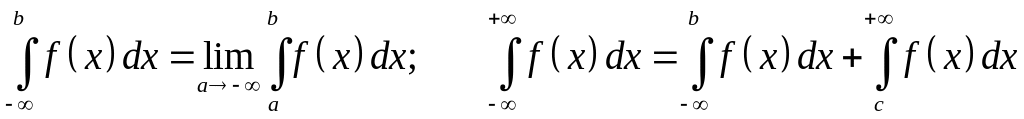 .
.
Поэтому дальше будем рассматривать только интеграл (30).
Теорема 27. (Критерий Коши). Для того, чтобы несобственный интеграл (30) был сходящимся необходимо и достаточно, чтобы
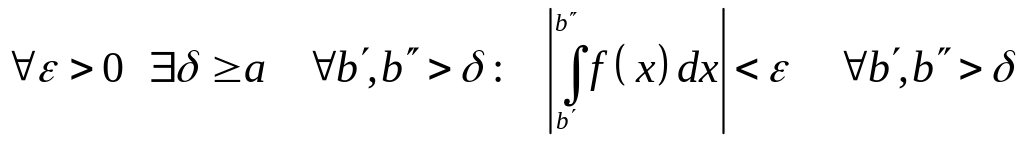
□ Сходимость
интеграла
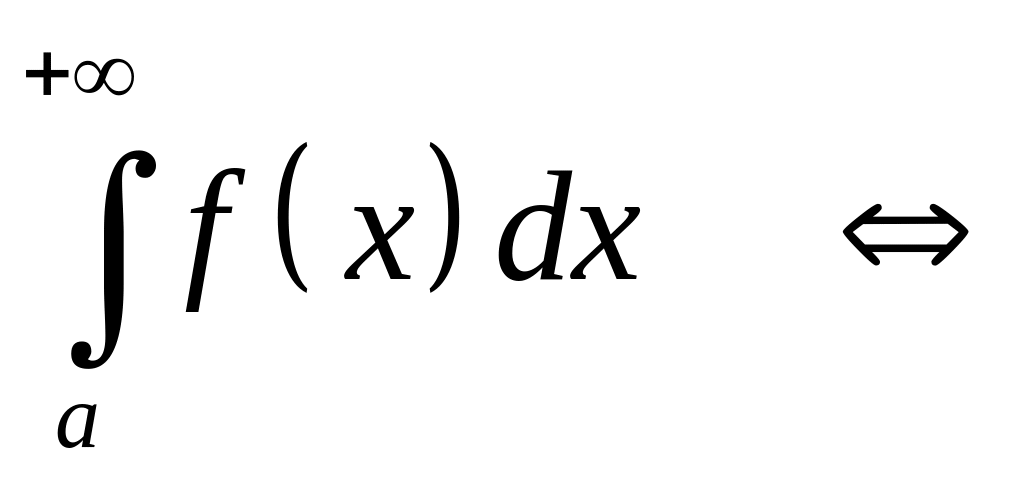 существованию конечного предела
существованию конечного предела
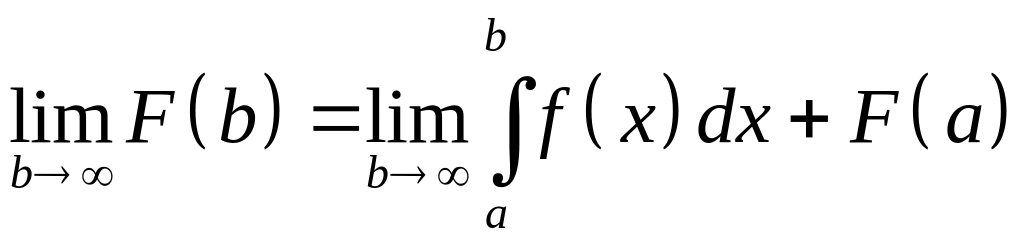 .
Но в силу критерия Коши для функции
.
Но в силу критерия Коши для функции
![]() при
при
![]() для существования предела необходимо
и достаточно, чтобы
для существования предела необходимо
и достаточно, чтобы
Тогда последнее неравенство можно переписать и виде:

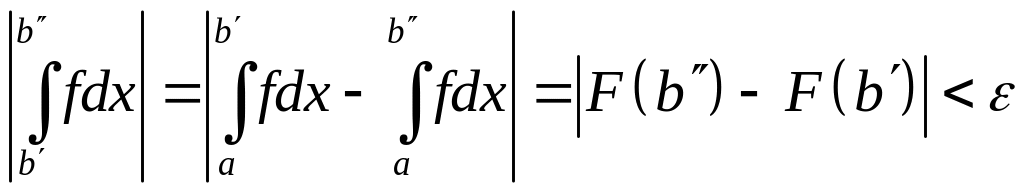 ■ Теорема
28. (Признак
сравнения). Пусть
■ Теорема
28. (Признак
сравнения). Пусть
а)
и
определены на
,
интегрируемы на
![]() ;
;
б)![]() при
при
![]() ;
;
в)
несобственный интеграл
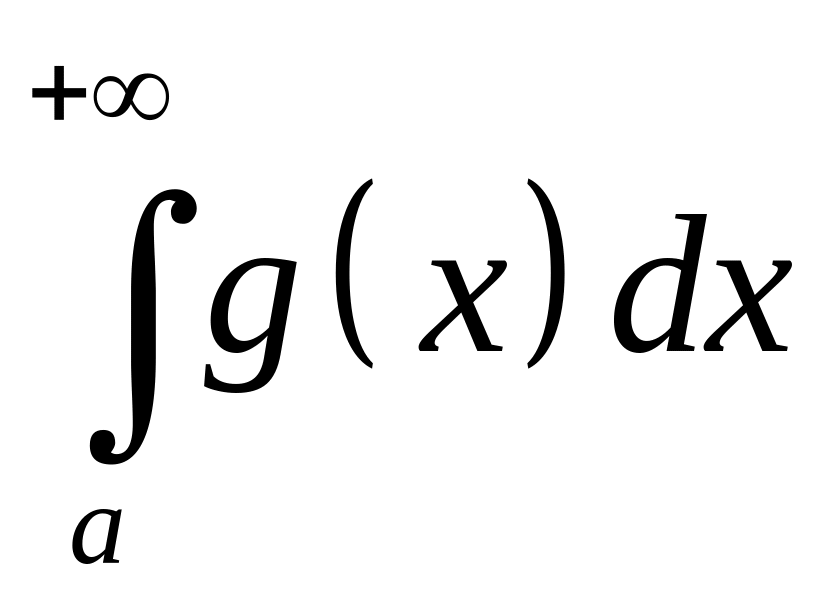 – сходится.
– сходится.
Тогда сходится и .
 Т.к.
сходится, то по теореме 27 выполняется:
Т.к.
сходится, то по теореме 27 выполняется:
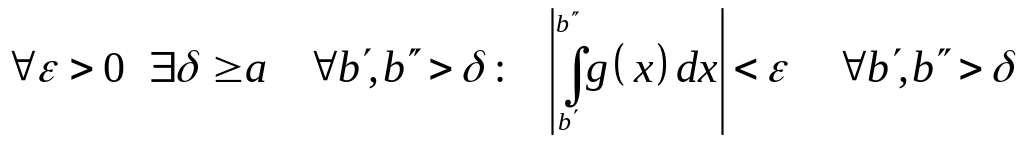 ,
,
Тогда проверим критерий Коши для :
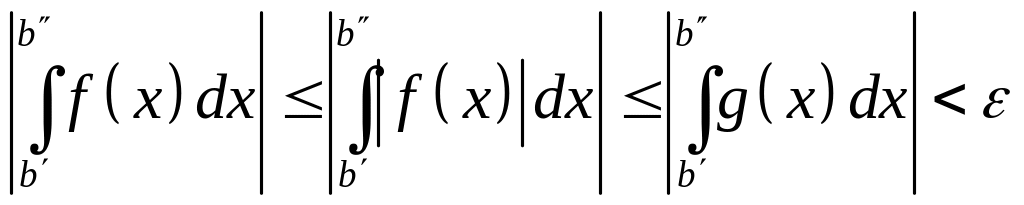 ■
■
Определение 6. Несобственный интеграл (30) называется абсолютно сходящимся, если сходится интеграл
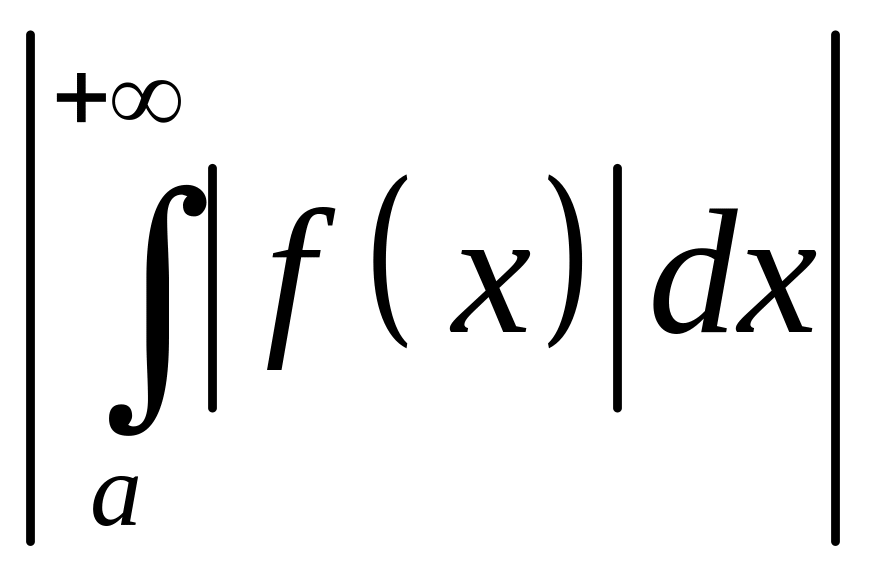 (31)
(31)
Если интеграл (30) сходится, а (31) расходится, то говорят, что интеграл (30) сходится условно. Из теоремы ясно, что если (30) абсолютно сходится, то и просто сходится.
Теорема
29. (Основной
критерий сходимости).
Пусть
![]() при
,
тогда для сходимости интеграла (25)
необходимо и достаточно, чтобы
при
,
тогда для сходимости интеграла (25)
необходимо и достаточно, чтобы
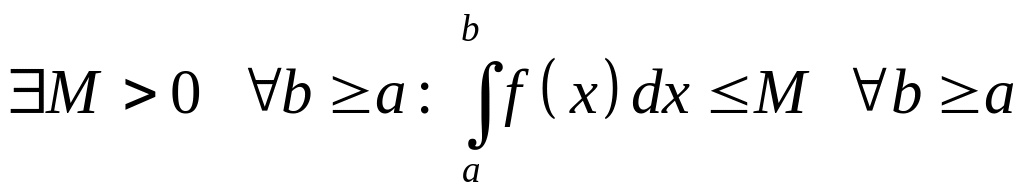 .
(32)
.
(32)
Функция
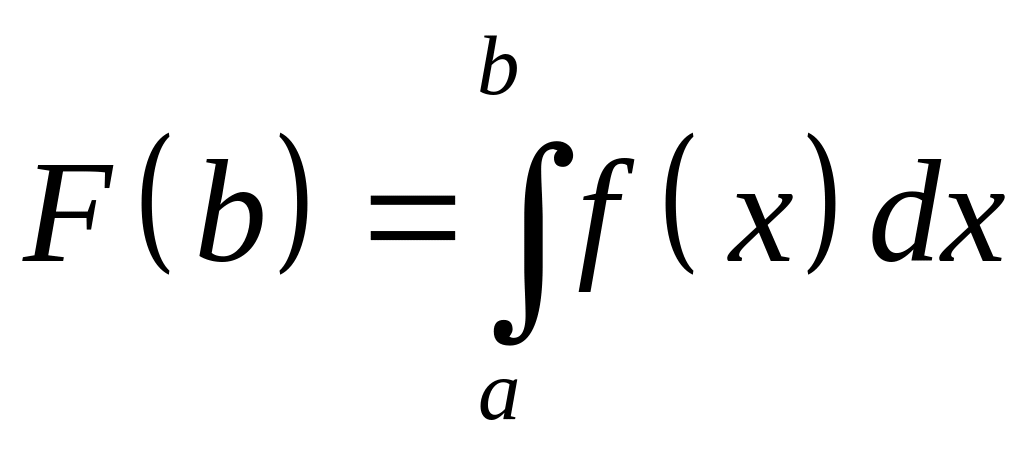 неубывает при
неубывает при
![]() ,
т.к. по условию
.
Поэтому для сходимости интеграла (30) ,
т.е. для существования предела необходимо
и достаточно, чтобы
была
ограничена сверху, т.е.
,
т.к. по условию
.
Поэтому для сходимости интеграла (30) ,
т.е. для существования предела необходимо
и достаточно, чтобы
была
ограничена сверху, т.е.
![]() при
при
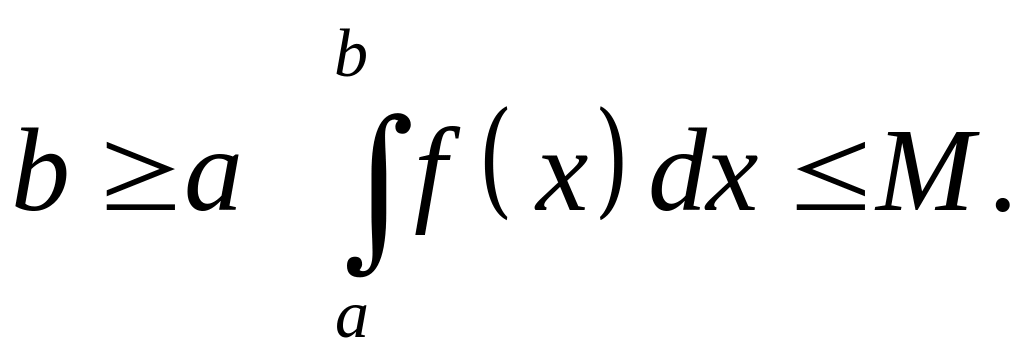 ■
■
Теорема
30.
Пусть
и
![]() возрастающая последовательность,
сходящаяся к
возрастающая последовательность,
сходящаяся к
![]() ,
тогда чтобы для сходимости интеграла
(1), необходимо и достаточно, чтобы
сходился числовой ряд
,
тогда чтобы для сходимости интеграла
(1), необходимо и достаточно, чтобы
сходился числовой ряд
 .
(33)
.
(33)
Рассмотрим
последовательность частичных сумм
![]() ряда (33). Очевидно, что
ряда (33). Очевидно, что
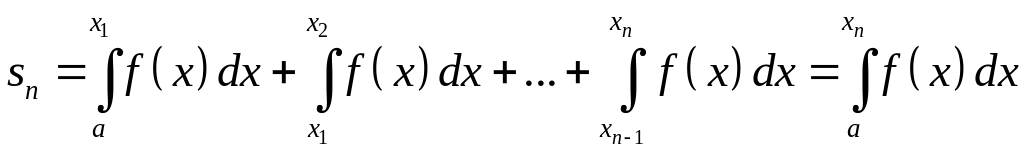
Последовательность
неубывает, т.к.
при
и
![]() .
.
Т.к.
![]() ,
то
,
то
![]() .
.
Тогда
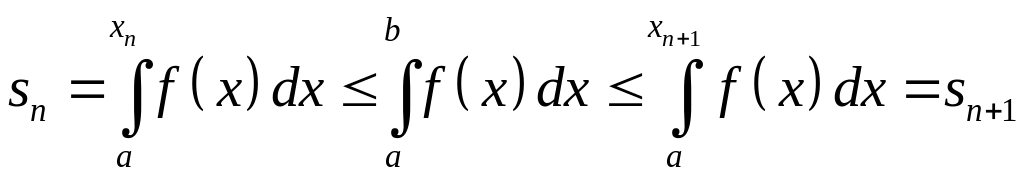 (34)
(34)
![]()
Если
(30) сходится, то в силу предыдущей теоремы
выполняется неравенство (32). Из неравенств
(32) и (34) следует, что
![]() при
при
![]() .
Поскольку
неубывающая последовательность, то она
сходится
.
Поскольку
неубывающая последовательность, то она
сходится
![]() ряд (33) сходится.
ряд (33) сходится.
Если
ряд (33) сходится, то последовательность
его частичных сумм ограничена сверху
![]() .
Очевидно и из (34)
что (32) выполняется при
.
В силу теоремы 28 интеграл (30) сходится.
■
.
Очевидно и из (34)
что (32) выполняется при
.
В силу теоремы 28 интеграл (30) сходится.
■
Теорема
31. (Интегральный
признак сходимости числового
ряда).
Пусть
невозрастающая положительная функция,
определенная при
![]() (
(![]() –натуральное число). Тогда ряд
–натуральное число). Тогда ряд
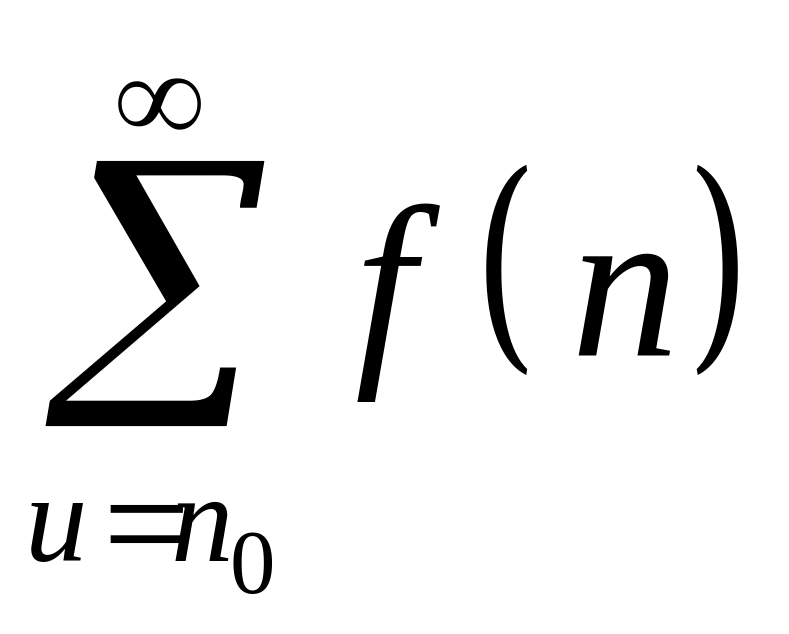 (35)
(35)
и
интеграл
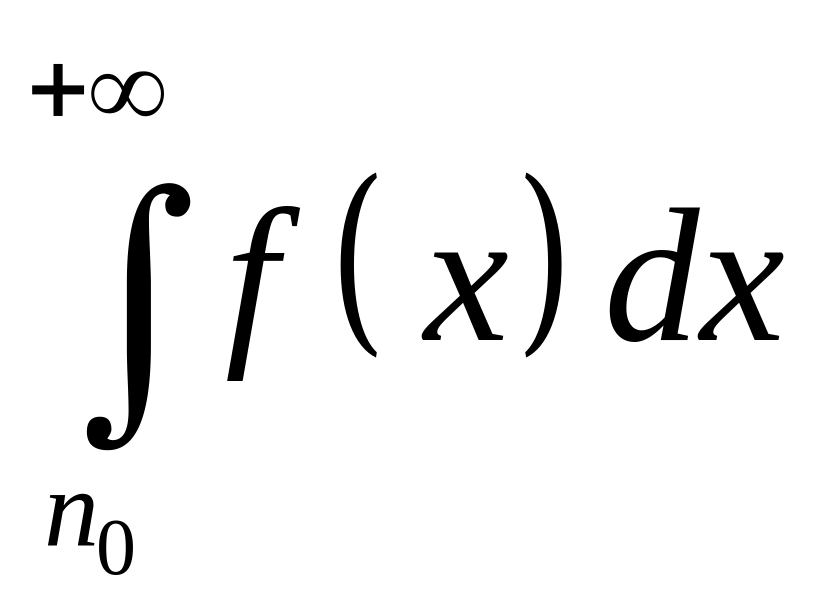 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
В
силу условий теоремы
![]() при
при
![]() .
Интегрируя неравенство почленно на
отрезке
.
Интегрируя неравенство почленно на
отрезке
![]() ,
получим
,
получим
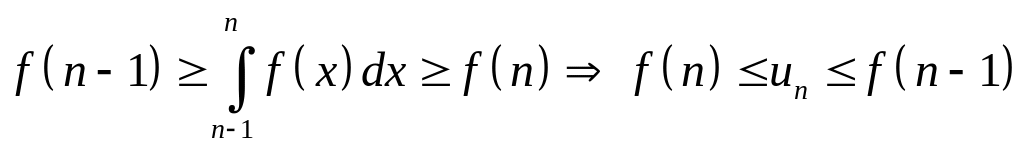 .
.
Из
этих неравенств, в силу признака сравнения
для числового ряда следует, что ряд (35)
сходится или расходится одновременно
с рядом
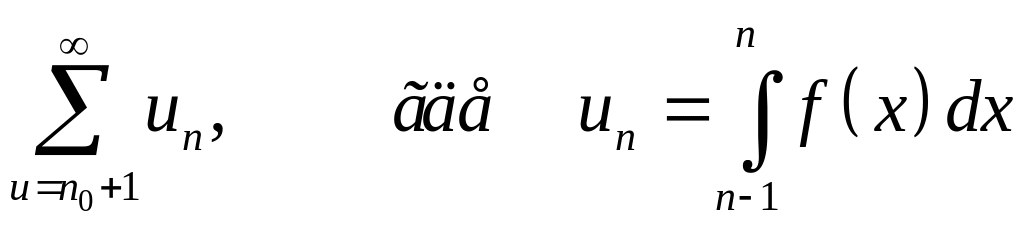 .
.
С
другой стороны, в силу теоремы (28) ряд
 сходится или расходится одновременно
с интегралом
.
■
сходится или расходится одновременно
с интегралом
.
■
Сформулируем теорему, которая позволяет в некоторых случаях установить условную сходимость несобственных интегралов.
Теорема 32. (Признак Дирихле). Пусть выполняются следующие условия:
а) Функция интегрируемая по Риману на любом отрезке
б)
 ;
;
в)
Функция
при
непрерывно дифференцируемая и монотонно
убывая
![]() при
при
![]() .
Тогда
.
Тогда
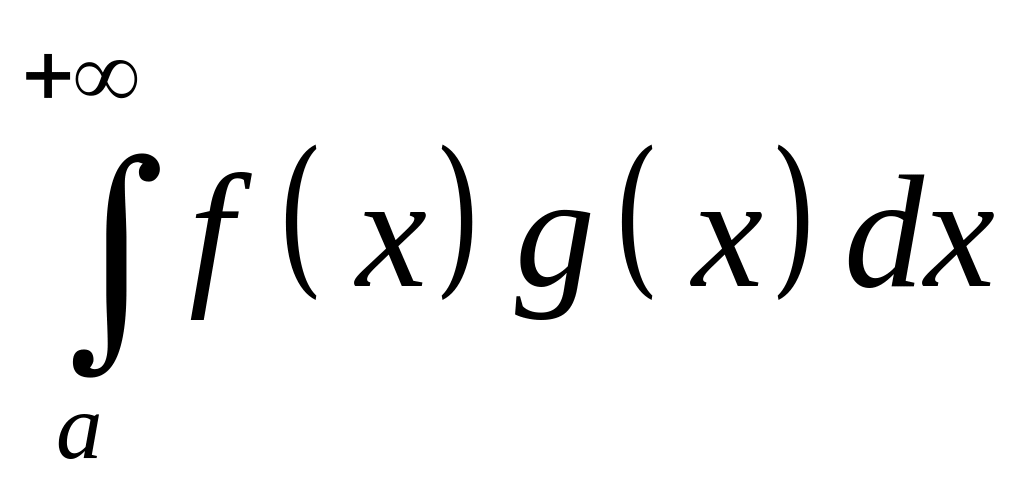 – сходится.
– сходится.
Рассмотрим
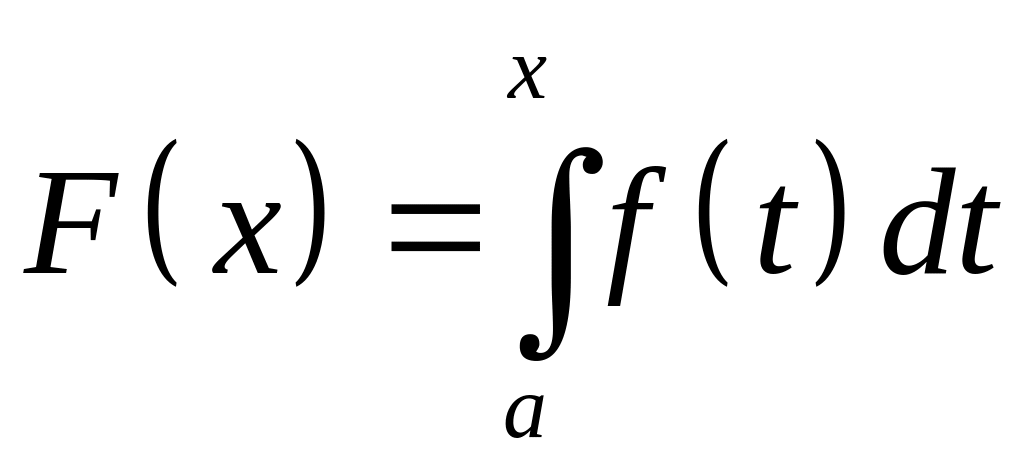 .
По условию теоремы
ограничена
.
По условию теоремы
ограничена
![]() ,
т.е.
,
т.е.
![]() (из условия (а)). Заметим, что
(из условия (а)). Заметим, что
![]() .
.
По формуле интегрирования по частям, имеем:
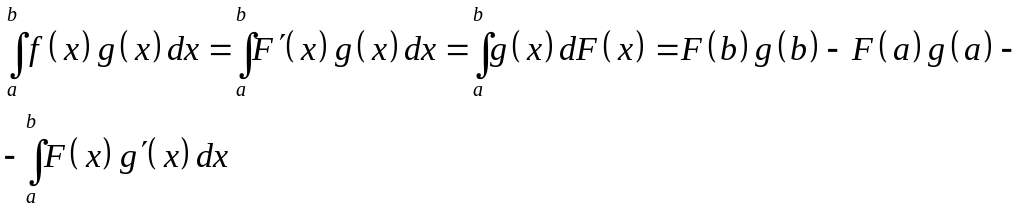
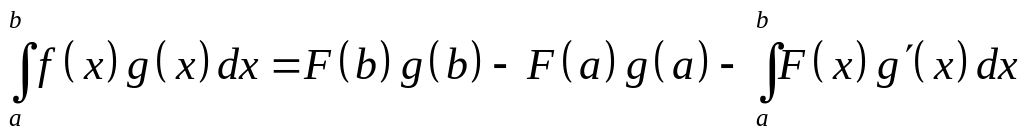 .
(36)
.
(36)
Рассмотрим
интеграл в правой части и оценим,
учитывая, что по условию (в)
монотонно убывает, а следовательно
![]() .
.
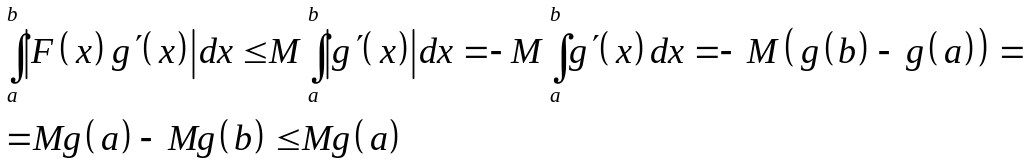
Следовательно,
из теоремы 28 несобственный интеграл
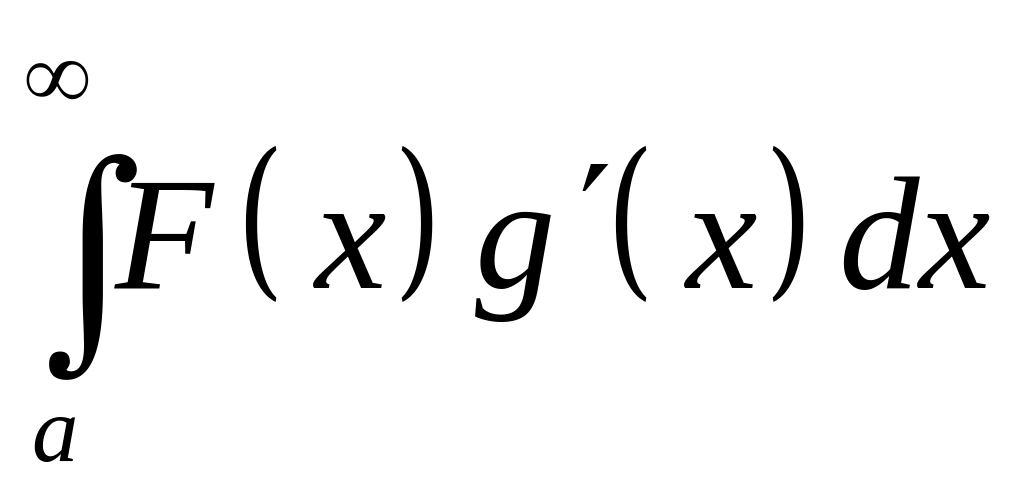 сходится абсолютно, а значит и просто
сходится. Следовательно, существует
конечный предел
сходится абсолютно, а значит и просто
сходится. Следовательно, существует
конечный предел
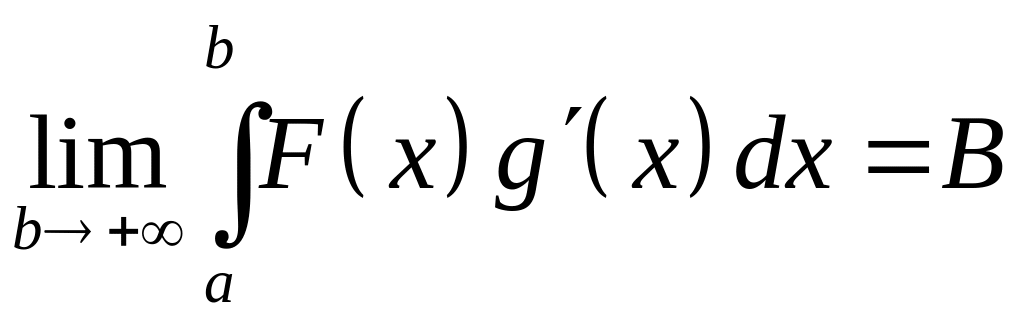 .Т.к.
.Т.к.
![]() и
и
![]() при
,
то
при
,
то
![]() .
.
С
ледовательно,
в правой части (36)
![]() пределы всех слагаемых.
■
пределы всех слагаемых.
■
Пример38.
![]() ,
т. е. данный интеграл сходится.
,
т. е. данный интеграл сходится.
Пример
39.
![]() ,
но придел функции
,
но придел функции
![]() при
при
![]() не существует, следовательно, интеграл
расходится.
не существует, следовательно, интеграл
расходится.
Пример
40.
![]() ;
интеграл расходится, так как
;
интеграл расходится, так как
![]() .
.
Пример
41.
![]() ,
,
![]() – некоторое число.
– некоторое число.
Если α≠1, то для любого
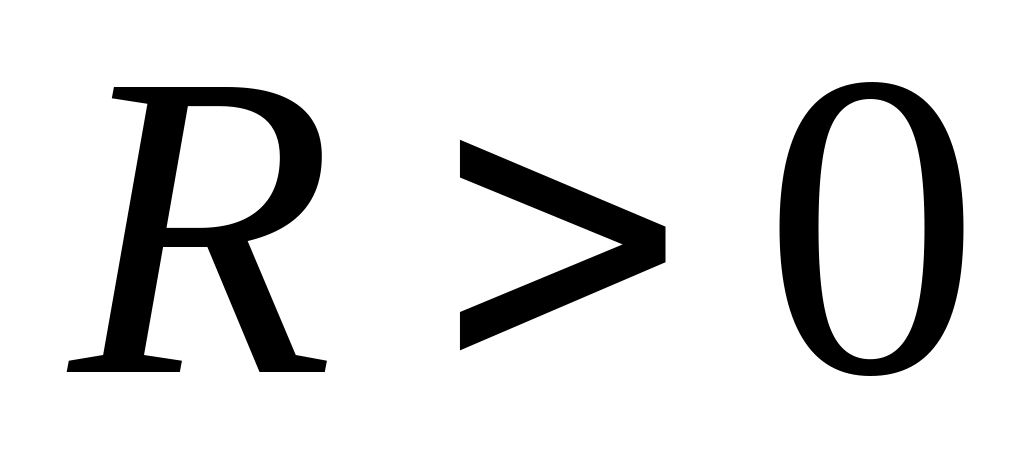
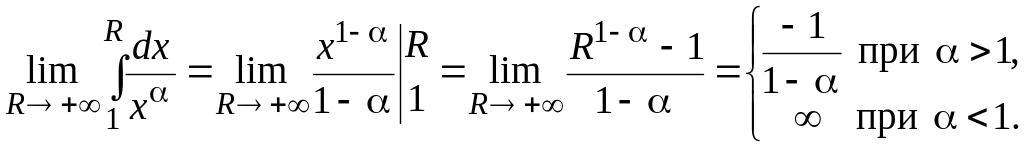
Если
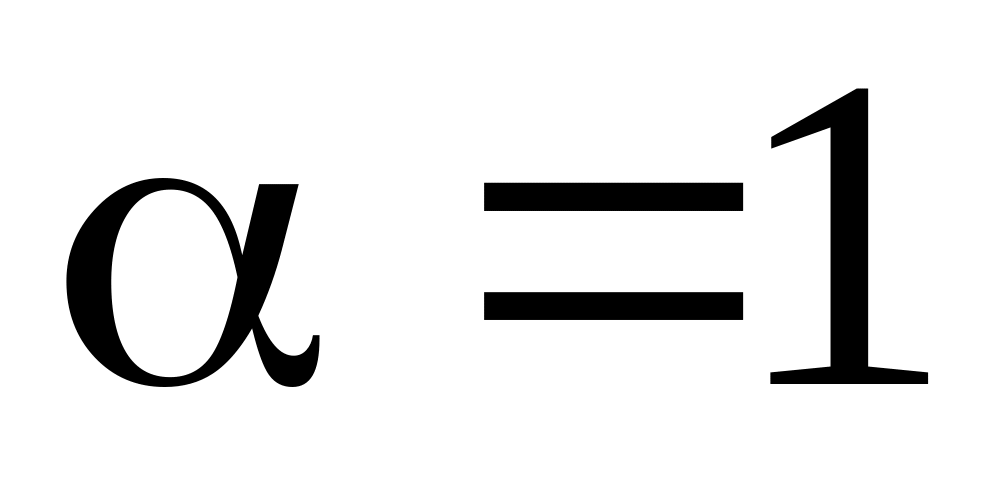 ,
то для любого
,
то для любого
![]() .
.
Таким
образом, данный интеграл сходится при
![]() и расходится при
и расходится при
![]() .
.
Заметим, что в рассмотренных примерах вычисление несобственного интеграла было основано на его определении. Теперь воспользуемся признаками сходимости.
Пример
42.
Исследовать сходимость
![]() .
.
□ Сравним
подынтегральную функцию
![]() с функцией
с функцией
![]() на промежутке
на промежутке
![]() .
Очевидно, что
.
Очевидно, что
![]() .
.
Но
интеграл
![]() сходится, так как
сходится, так как
![]() .
Следовательно,
согласно признаку сравнения сходится
и данный интеграл. ■
.
Следовательно,
согласно признаку сравнения сходится
и данный интеграл. ■
Пример
43.
Исследовать сходимость
![]() .
.
□ Сравнивая
подынтегральную функцию
![]() ,
с функцией
,
с функцией
![]() на промежутке
,
имеем
на промежутке
,
имеем
![]() .
.
Но
интеграл
![]() расходится, так как
расходится, так как
![]() (пример 39). Следовательно, согласно
признаку сравнения и данный интеграл
расходится.■
(пример 39). Следовательно, согласно
признаку сравнения и данный интеграл
расходится.■
Пример
44. Интеграл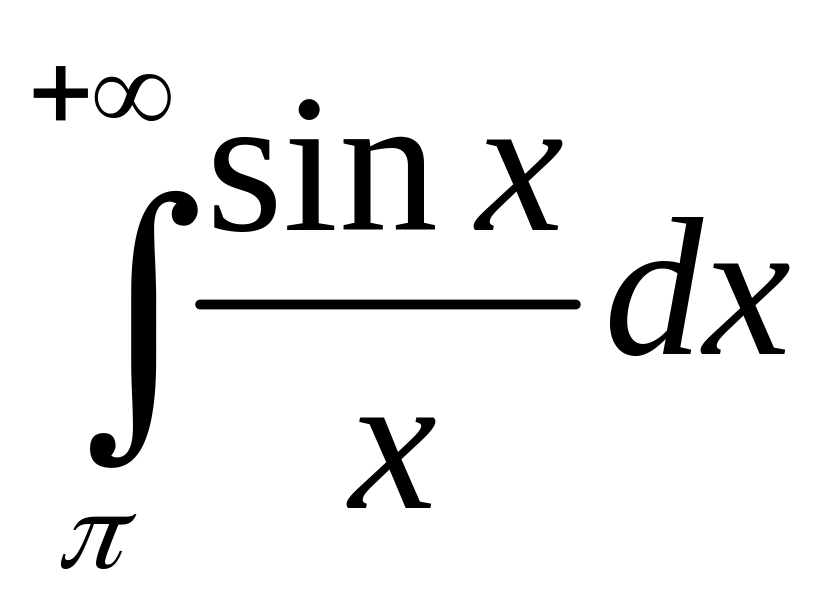 по
признаку Дирихле сходится, т.к.: а)
по
признаку Дирихле сходится, т.к.: а)
 ,
б)
,
б)
![]() непрерывно дифференцируемая и монотонно
убывает при
.Но
он сходится условно. Рассмотрим ряд
непрерывно дифференцируемая и монотонно
убывает при
.Но
он сходится условно. Рассмотрим ряд
![]() ,
где
,
где
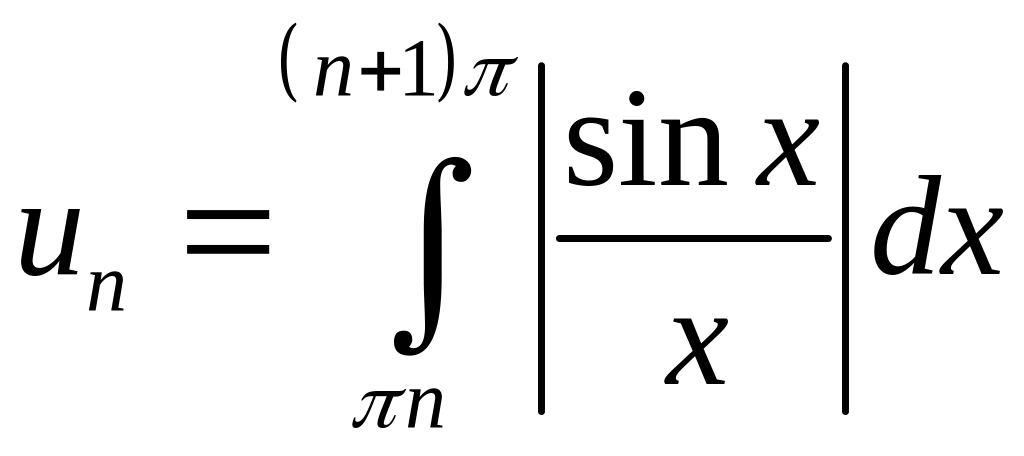 .
.
Ряд
расходится, т.к.
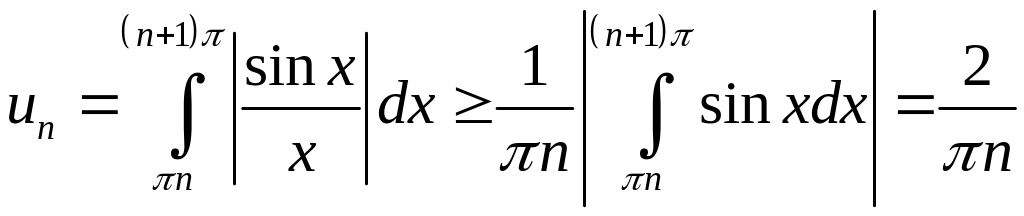 .
Но ряд
.
Но ряд
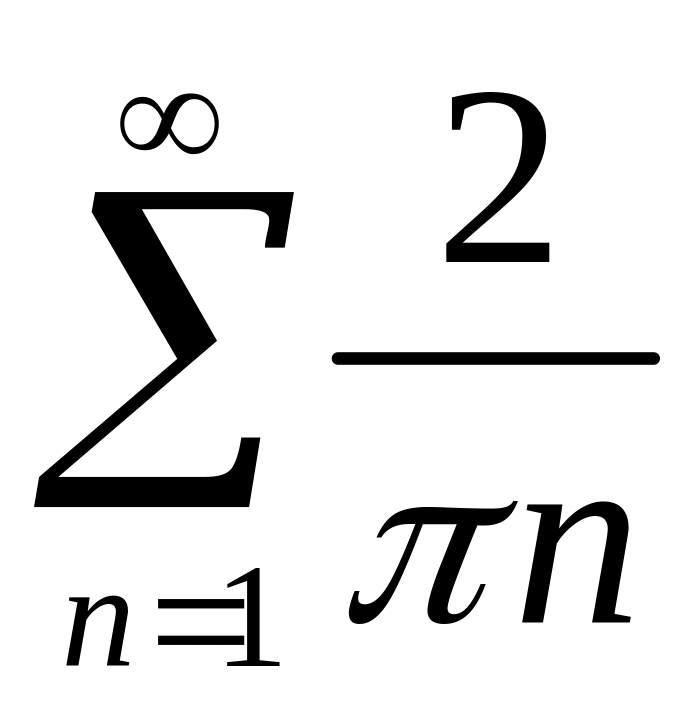 – расходится. Отсюда в силу теоремы 29
интеграл
– расходится. Отсюда в силу теоремы 29
интеграл
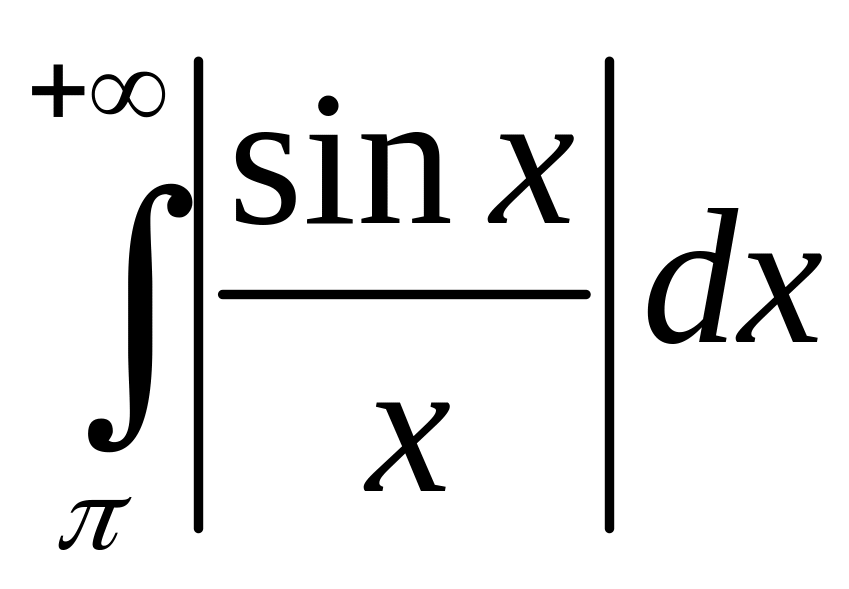 – расходится.
– расходится.
Заметим,
что если функцию
![]() доопределить в точке
доопределить в точке
![]() единицей, т.е.
единицей, т.е.
![]() ,
то она будет непрерывна на
,
то она будет непрерывна на
![]() .
Тогда
.
Тогда
 также сходится условно.
также сходится условно.
Несобственные интегралы от неограниченных функций.
Определение
7. Пусть
определена на промежутке
![]() ,
неограниченна на этом промежутке и
интегрируема по Риману на
,
неограниченна на этом промежутке и
интегрируема по Риману на
![]() .
Если
конечный предел
.
Если
конечный предел
 ,
то его называют несобственным
интегралом
и обозначается
,
то его называют несобственным
интегралом
и обозначается
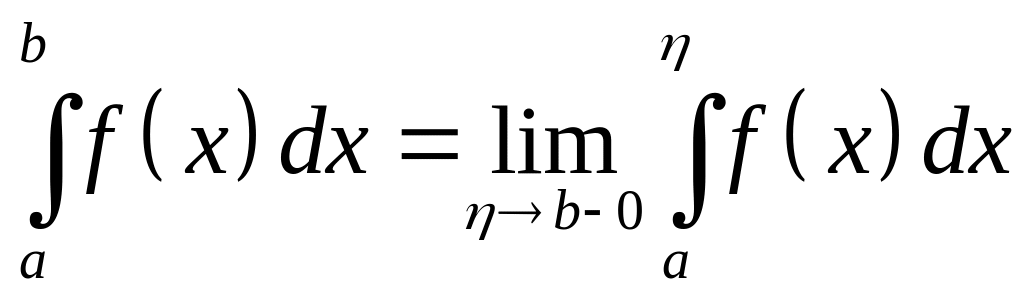 (37)
(37)
Говорят также, что несобственный интеграл (37) сходится на отрезке , а называют интегрируемой в несобственном смысле на . Если предел (37) не существует, то говорят, что интеграл расходится.
Замечания.
1)
Если
![]() ,
то интегралы
,
то интегралы
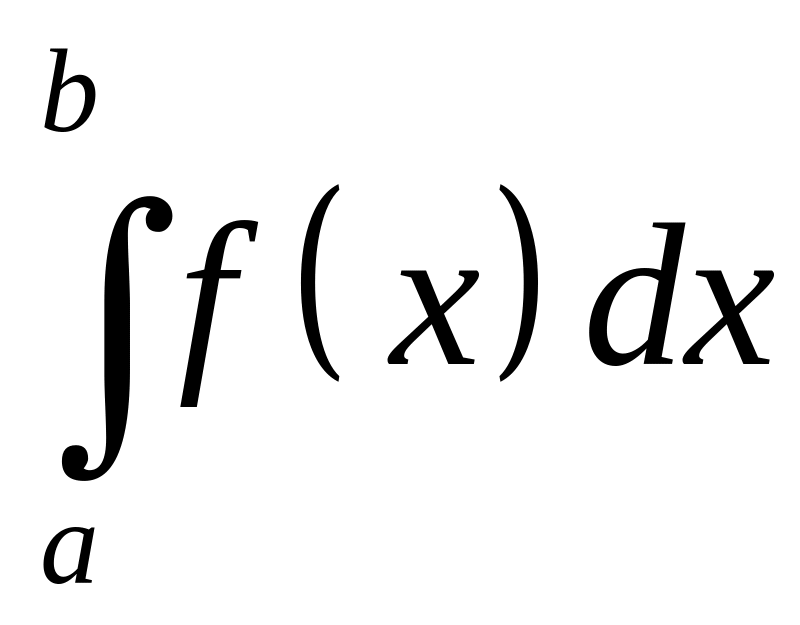 и
и
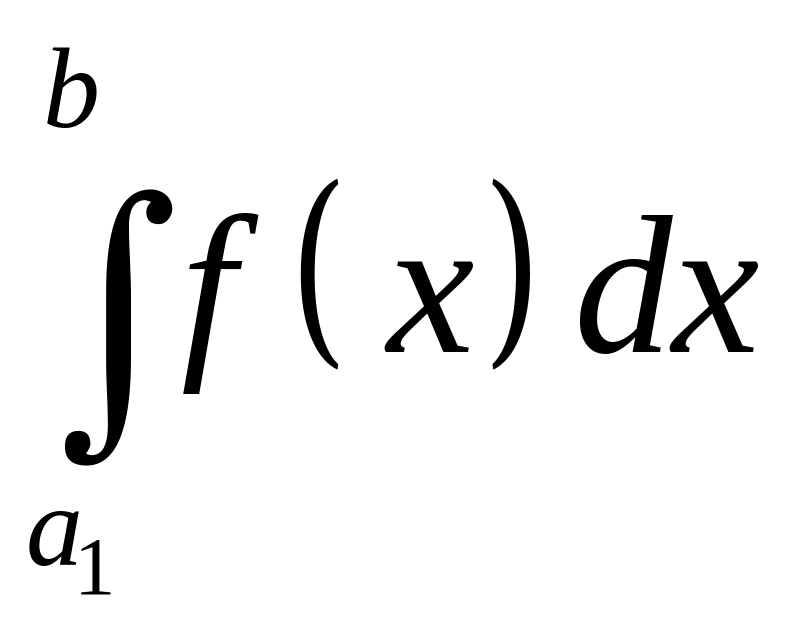 сходятся или расходятся одновременно,
т.к.
сходятся или расходятся одновременно,
т.к.
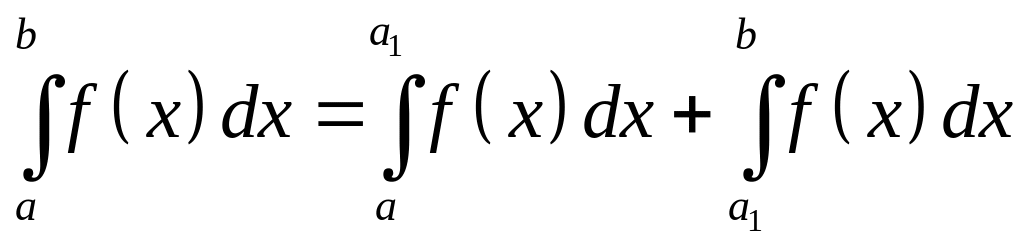 ,
то пределы
и
,
то пределы
и
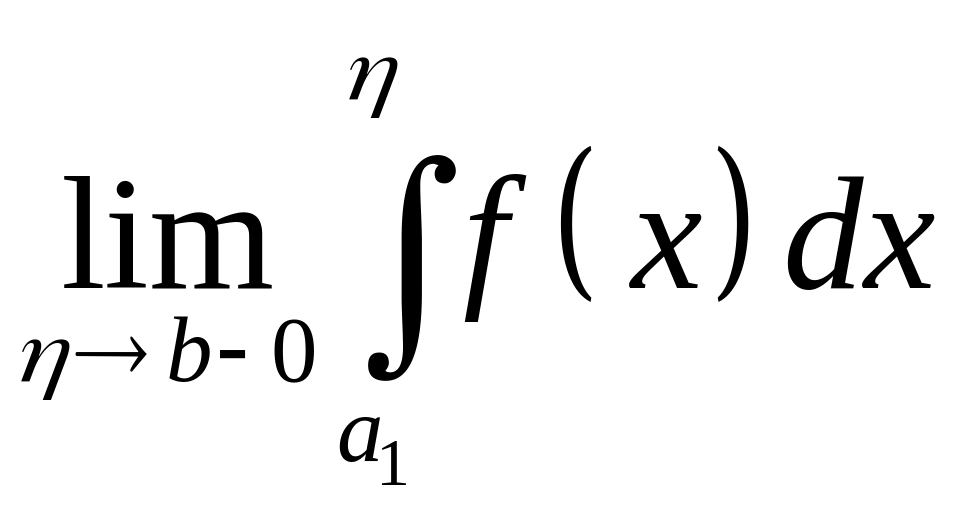 существуют одновременно.
существуют одновременно.
Формулу (37) иногда записывают в виде
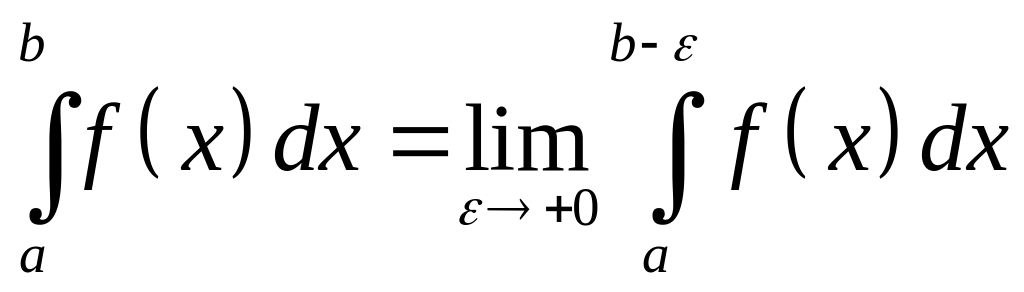
Если имеет первообразную на , то
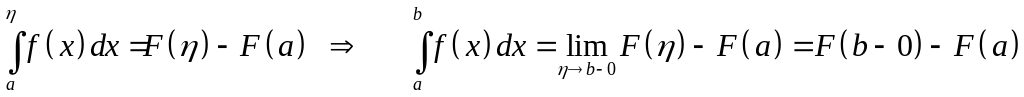
Аналогично определяется несобственный интеграл , если определена на
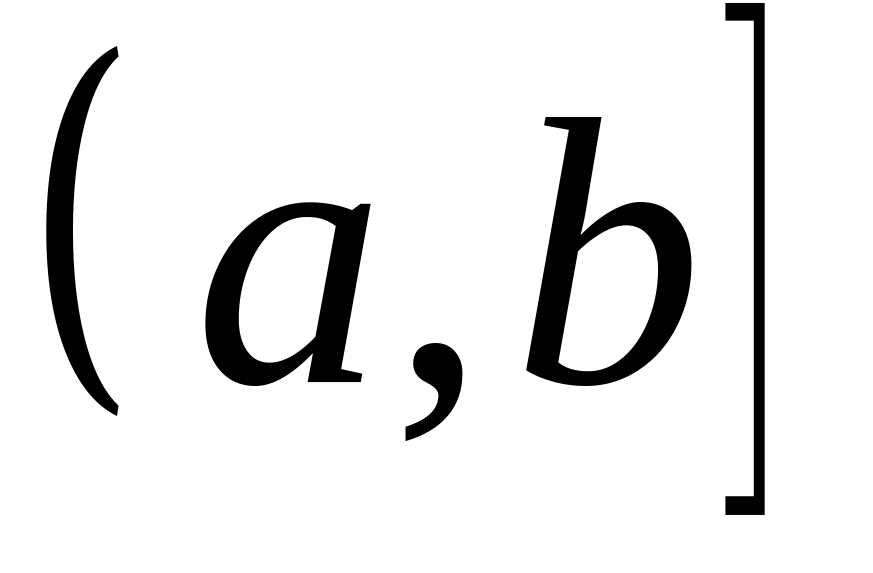 ,
неограниченна на нем и интегрируемая
,
неограниченна на нем и интегрируемая
 .
.
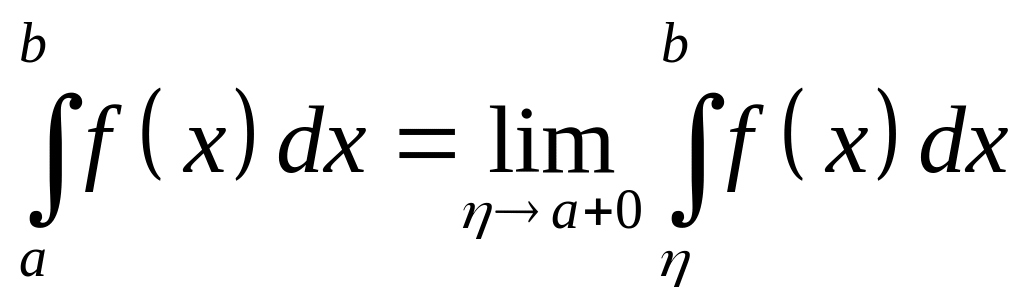 .
.
Если определена на
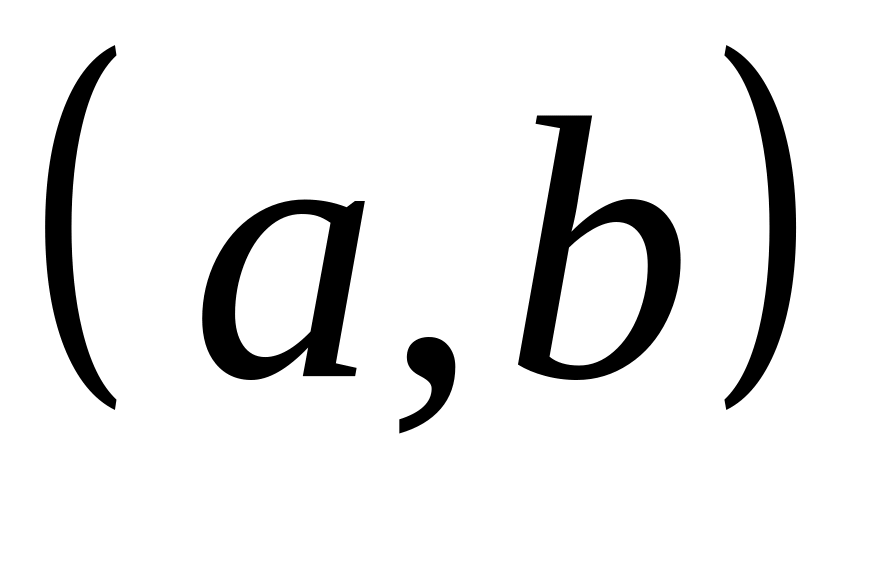 и сходятся
и сходятся
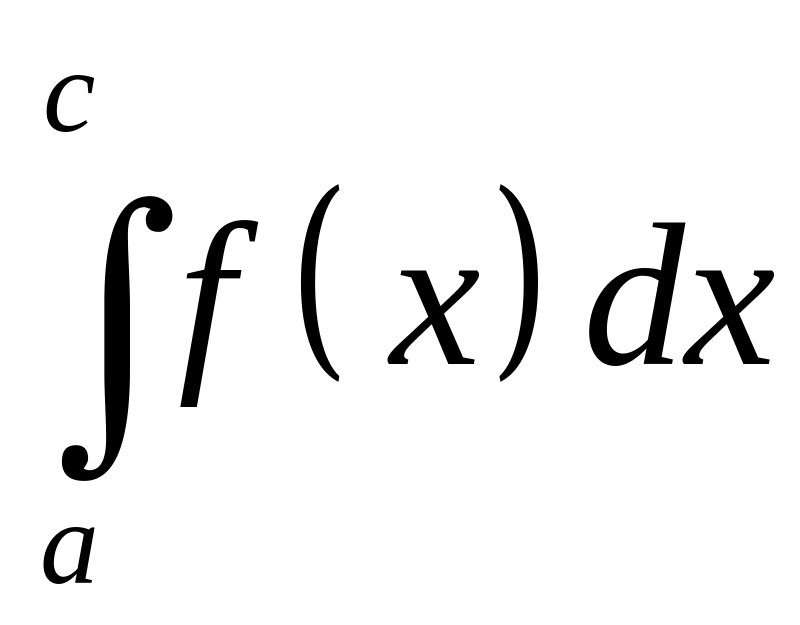 и
и
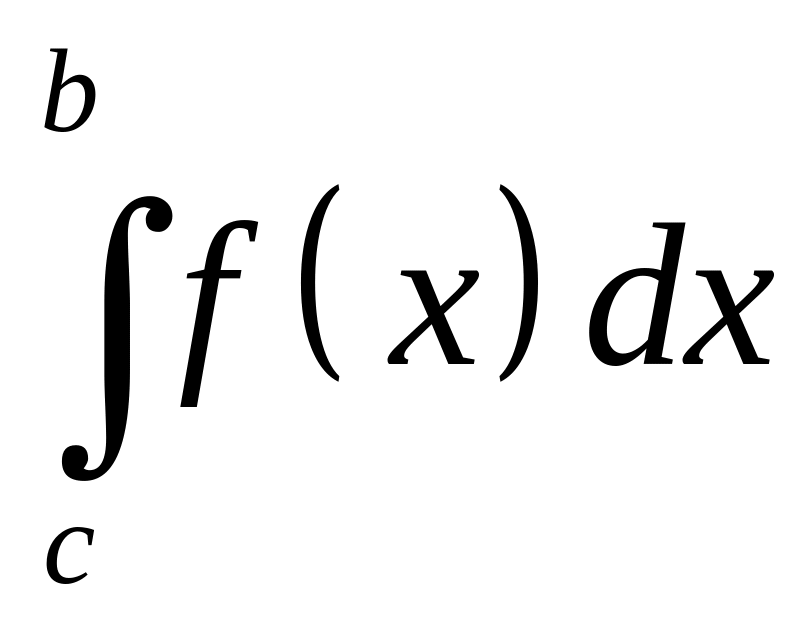 ,
то полагают по определению
,
то полагают по определению
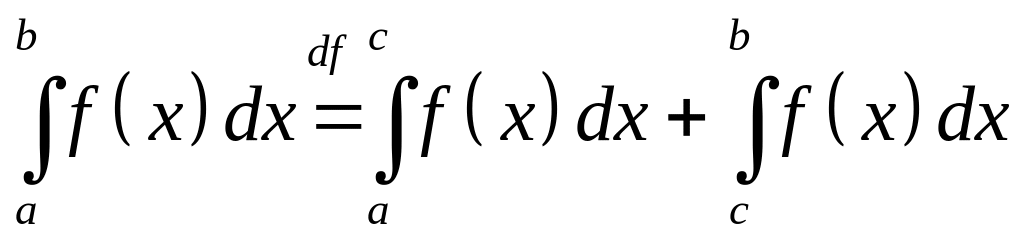 .
.
Имеют место следующие теоремы, которые доказываются также, как соответствующие теоремы для несобственных интегралов с бесконечными пределами.
Теорема 33. (Критерий Коши). Для того чтобы несобственный интеграл (37) был сходящимся, необходимо и достаточно, чтобы

Теорема
34. (Признак
сравнения).
Пусть
![]() и несобственный интеграл
и несобственный интеграл
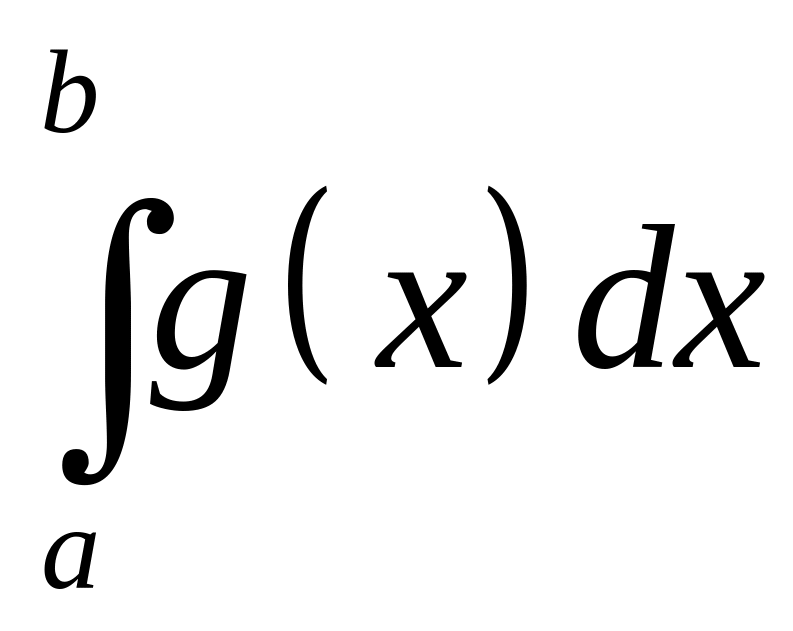 сходится, тогда сходится и интеграл
.
сходится, тогда сходится и интеграл
.
Из этой теоремы следует, что если интеграл сходится абсолютно, то он сходится.
Теорема
35. Пусть![]() ,
тогда для сходимости интеграла (7)
необходимо и достаточно, чтобы существовало
такое
,
тогда для сходимости интеграла (7)
необходимо и достаточно, чтобы существовало
такое
![]() ,
что при
,
что при
![]() имело место неравенство, т.е.
имело место неравенство, т.е.
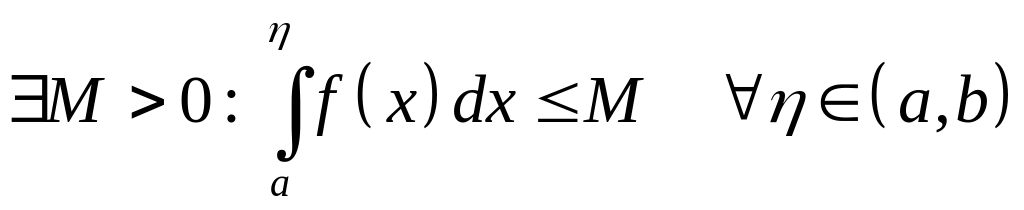 .
.
Пример
45.
![]() ,
,
![]() – некоторое число.
– некоторое число.
Если
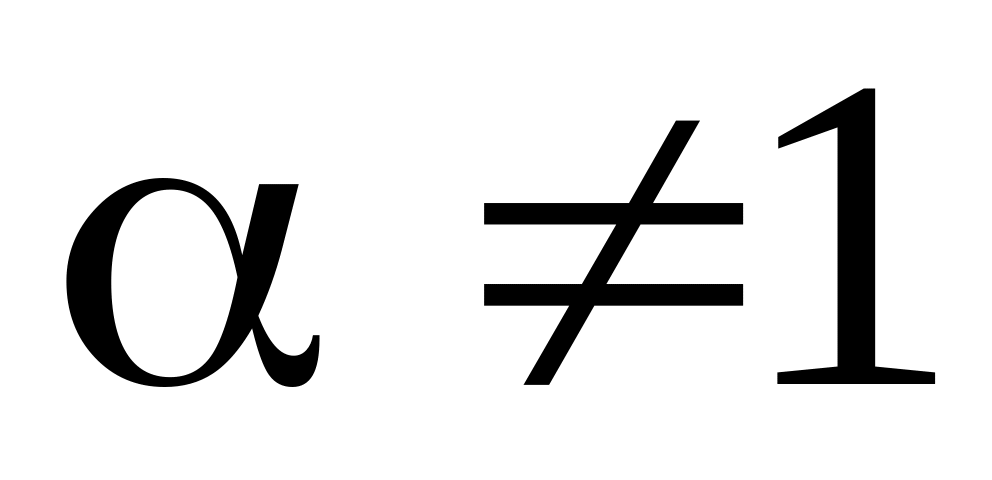 ,
то
,
то

Если , то
![]() .
.
Ясно,
что при
![]() этот интеграл существует как интеграл
Римана, при
этот интеграл существует как интеграл
Римана, при
![]() он сходится, а при
он сходится, а при
![]() расходится.
расходится.
Понятие
главного значения несобственного
интеграл.
Пусть
определена на всей числовой прямой
![]() и интегрируема по Риману на любом отрезке
и интегрируема по Риману на любом отрезке
![]() .
.
Определение
8.
Главным
значением
несобственного интеграла с
![]() пределами
называется предел (если он существует)
пределами
называется предел (если он существует)
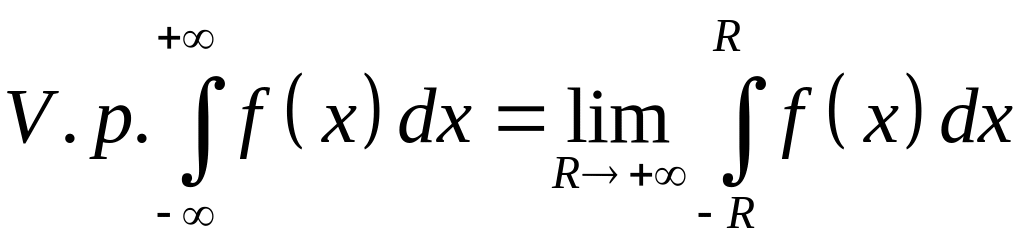
Пример
46. Легко
проверить, что
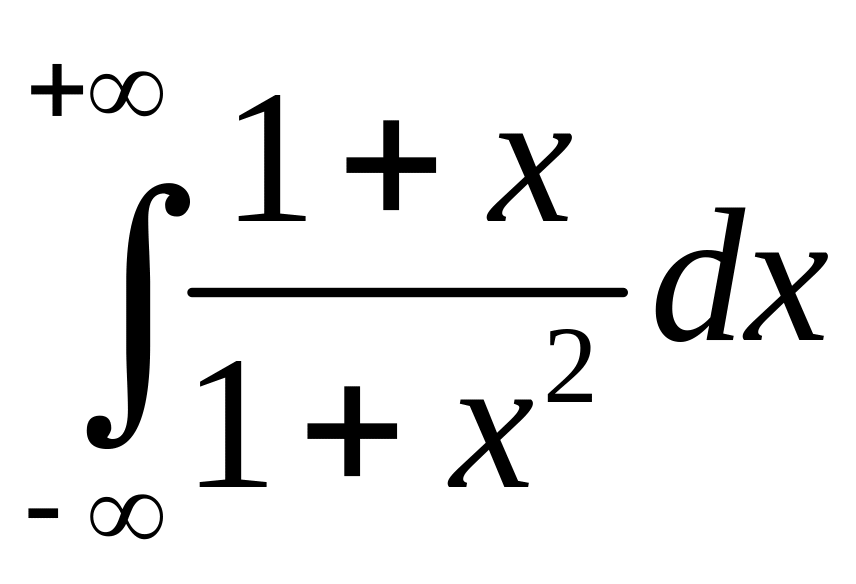 расходится. Найдем главное значение.
расходится. Найдем главное значение.
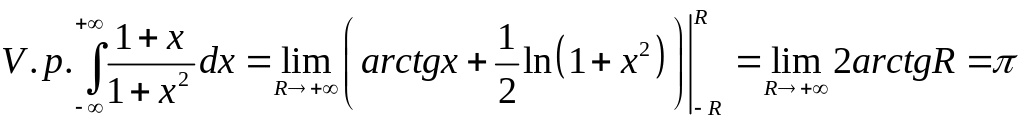
Определение
9. Пусть
определена
на
кроме
того
![]() и интегрируема на любом отрезке
и интегрируема на любом отрезке
![]() и
и
![]()
Главным
значением
несобственного
интеграла от разрывной в точке
![]() функции
называется
предел
функции
называется
предел
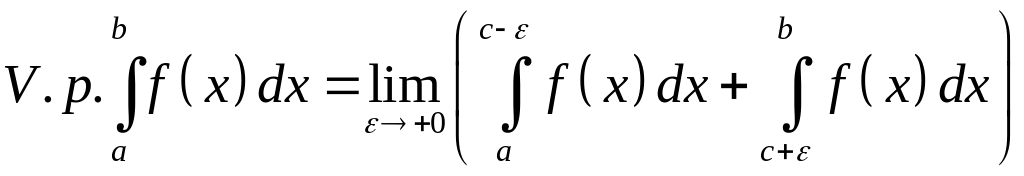
Пример
47. Интеграл
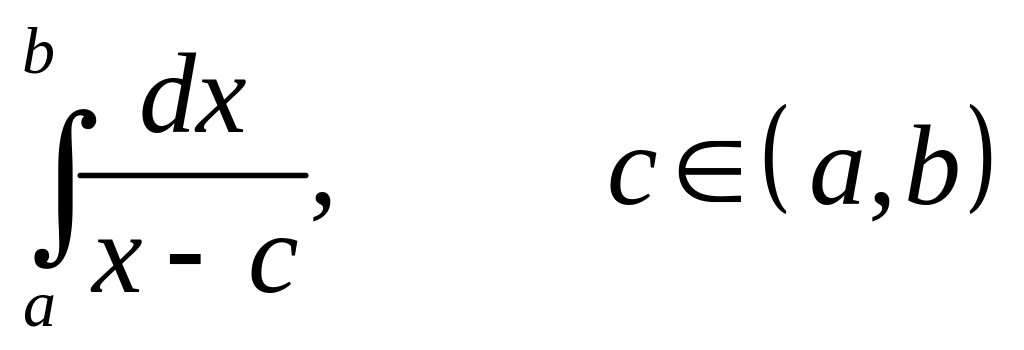 – расходится, но
– расходится, но