Интегралы, зависящие от параметра

9.5.1. Собственные интегралы, зависящие от параметра. Рассмотрим следующий интеграл:

. (28)

Предполагается, что интеграл в правой части существует как интеграл Римана. Переменная у называется параметром.

Теорема 15. Если функция непрерывна на замкнутом прямоугольнике , то функция непрерывна на отрезке .

‰ Пусть - произвольная точка на отрезке , функция , непрерывная на прямоугольнике П, равномерно непрерывна на нем (по теореме Кантора). Из равномерной непрерывности следует, что и для и такого, что выполняется . Тогда

.

Таким образом, получаем, что для , удовлетворяющему условию существует предел , т.е. непрерывна на . <

Следствие. Если непрерывна на П, то выполняется равенство:

.

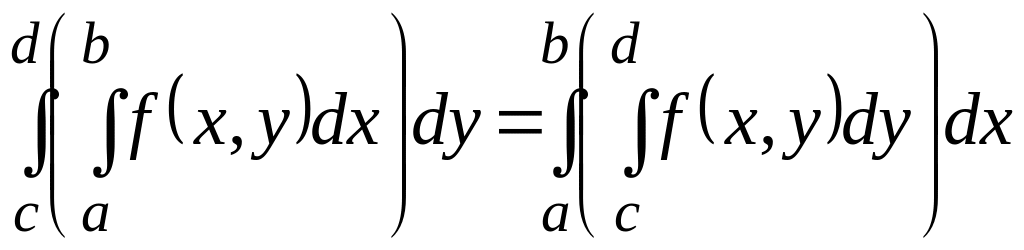Доказательство следует из теоремы 15 и из теоремы для заданной на области П и интегрируемой на . (см. «Вычисление двойного интеграла»).

Теорема 16. Если функция и её частные производные непрерывны на прямоугольнике П, то функция непрерывно дифференцируема на отрезке и

или ,

т.е. интеграл (40), зависящий от параметра, можно дифференцировать по параметру.

‰ Пусть , . В силу следствия к теореме 27 имеем

.

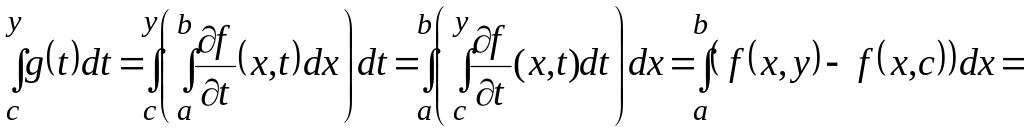
Получаем, что .

Тогда по правилу дифференцирования интеграла с переменным верхним пределом будет:

,

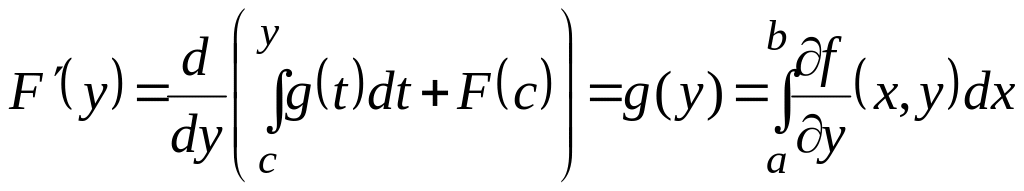причём в силу теоремы 27 непрерывна на . <

Следствие. Пусть и непрерывны на П, а функции и дифференцируемы на отрезке , причём и для . Тогда справедлива формула

.

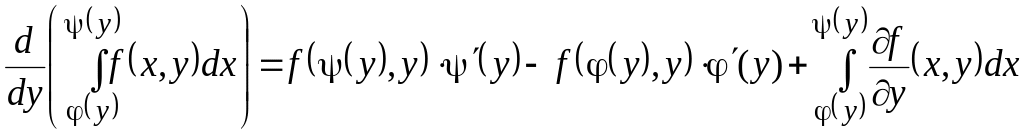Эта формула называется формулой дифференцирования интеграла с переменными пределами интегрирования.

‰ Рассмотрим функцию 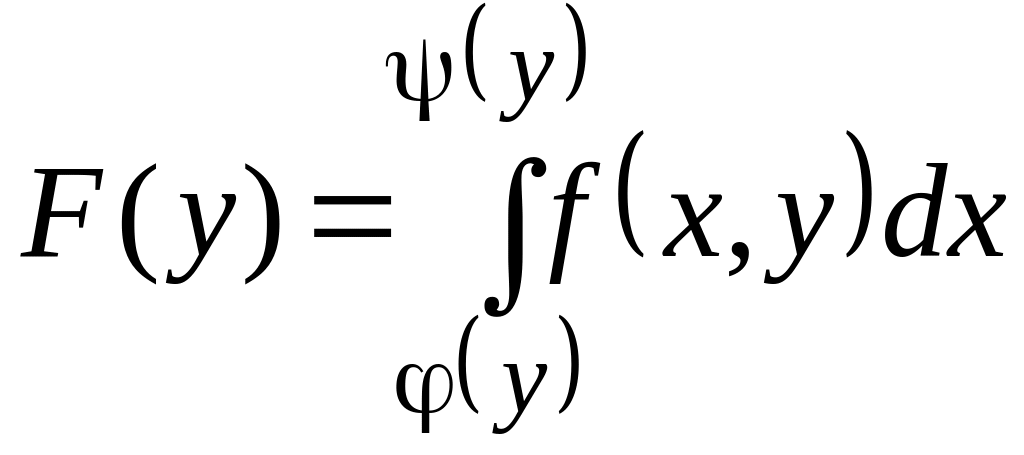, . Запишем её как сложную функцию , где , и найдём как производную сложной функции у:

.

Так как

;

;

,

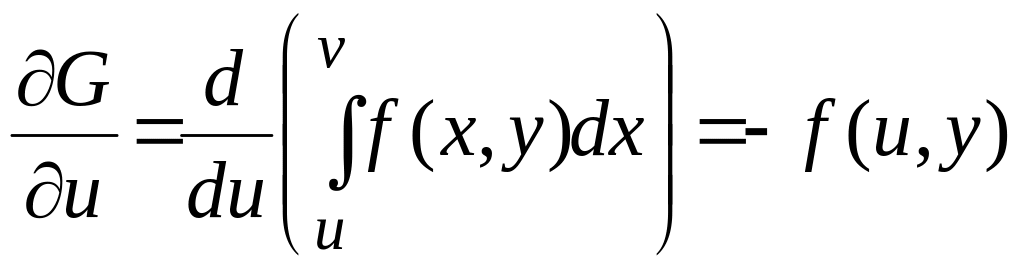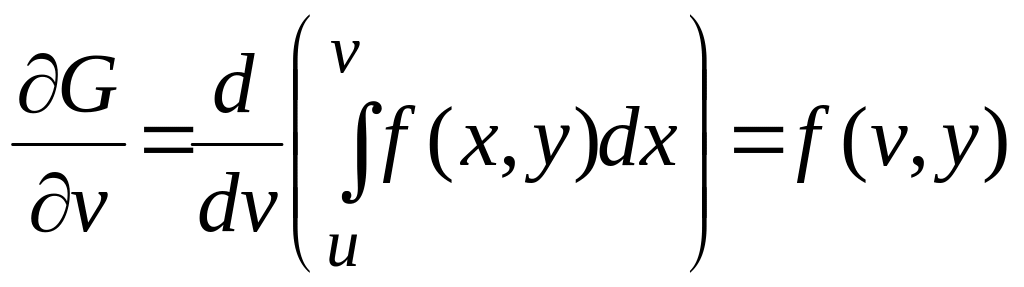то, подставляя полученные выражения для производных в формулу для вычисления , получаем доказываемую формулу. ■

9.6.2. Несобственные интегралы, зависящие от параметра. Пусть функция определена на множестве . Будем рассматривать интегралы вида:

. (29)

Пусть несобственный интеграл (29) сходится. В этом случае говорят, что несобственный интеграл сходится на отрезке .

Легко увидеть из признака Коши для несобственных интегралов, что интеграл (29) сходится в том и только в том случае, когда существует предел . Это означает, что для такое, что для выполняется

Определение 5. Несобственный интеграл (29) называется равномерно сходящимся на , если для такое, что выполняется .

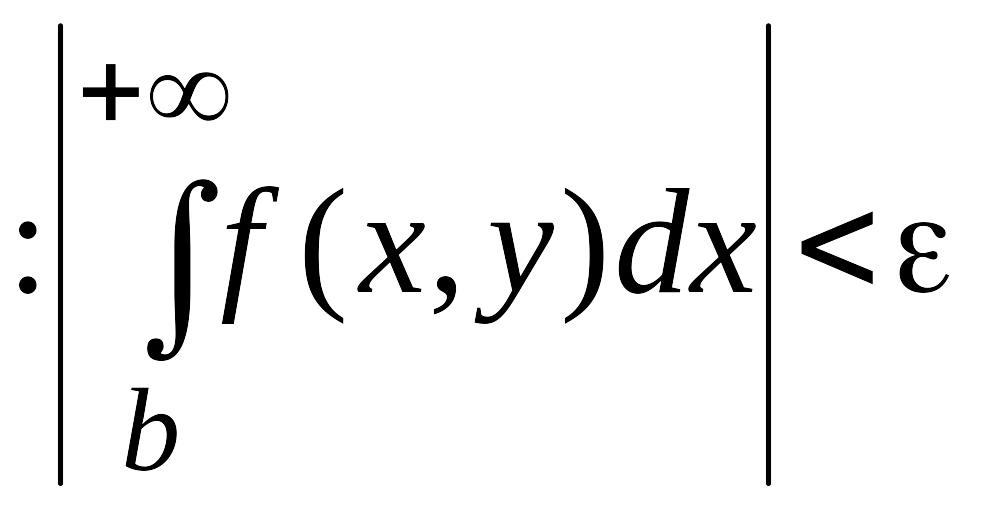Таким образом, в отличие от определения простой сходимости требуется, чтобы число В было зависящим только от и не зависит и не зависит от у.

Теорема 17. (Признак Вейерштрасса). Пусть:

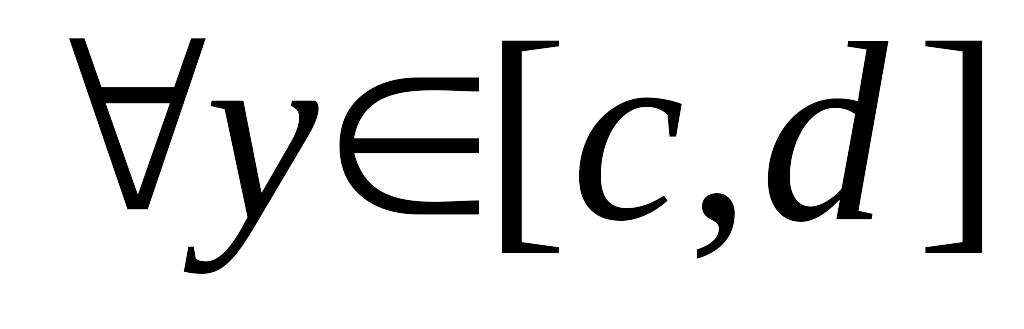1. функция 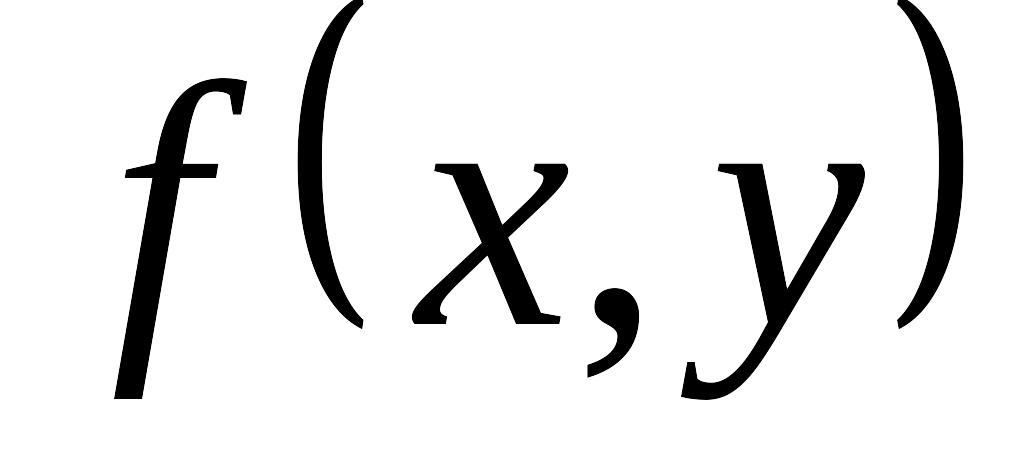интегрируема по Риману по переменной х на любом отрезке ;

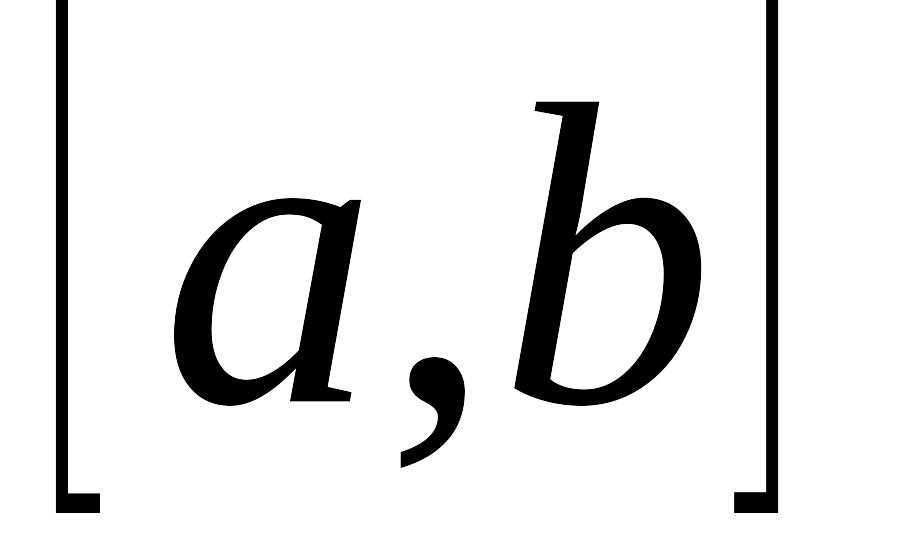2. функция 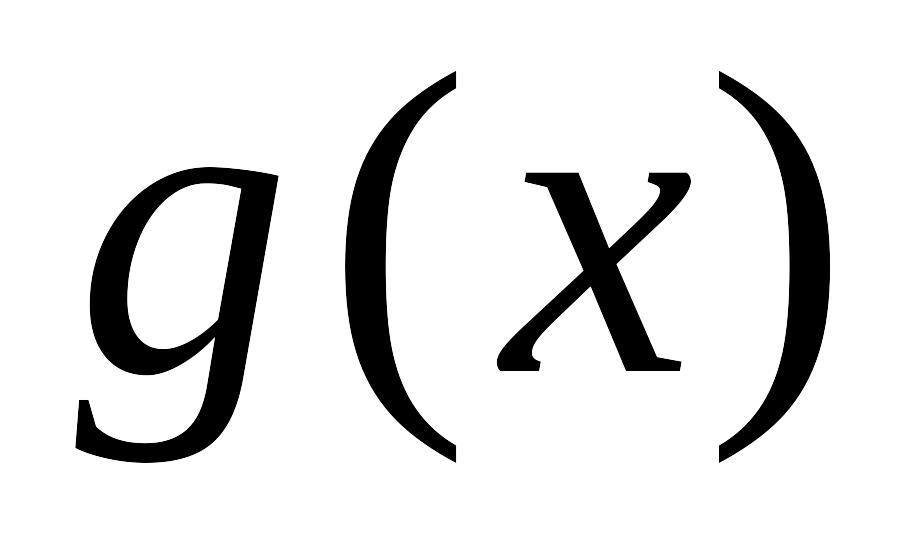определена на промежутке , причём 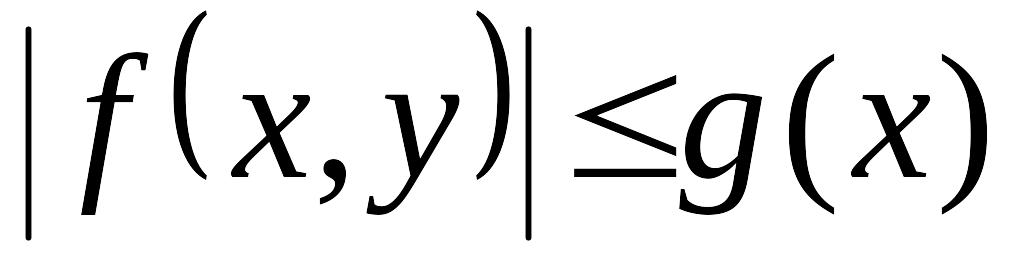для 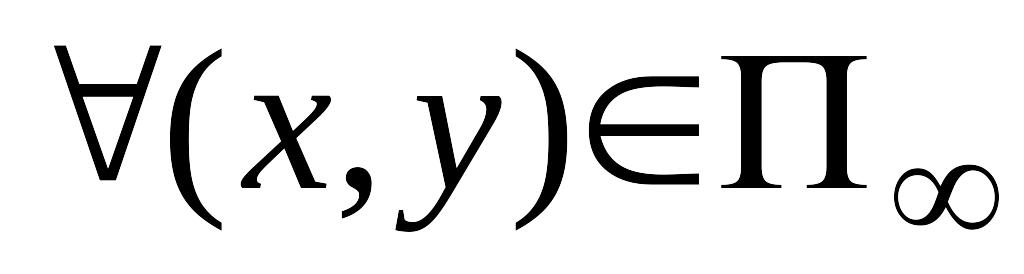; (30)

3) интеграл 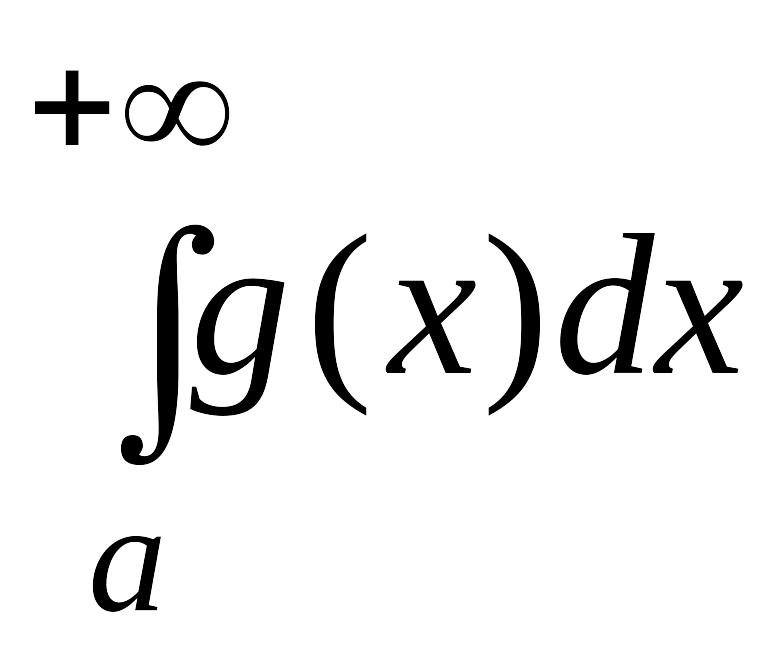сходится,

тогда несобственный интеграл (29) сходится абсолютно и равномерно на .

‰ По признаку сравнения для несобственных интегралов в силу (30) несобственный интеграл (29) сходится абсолютно.

Из сходимости интеграла (29) следует, что такое, что для выполняется 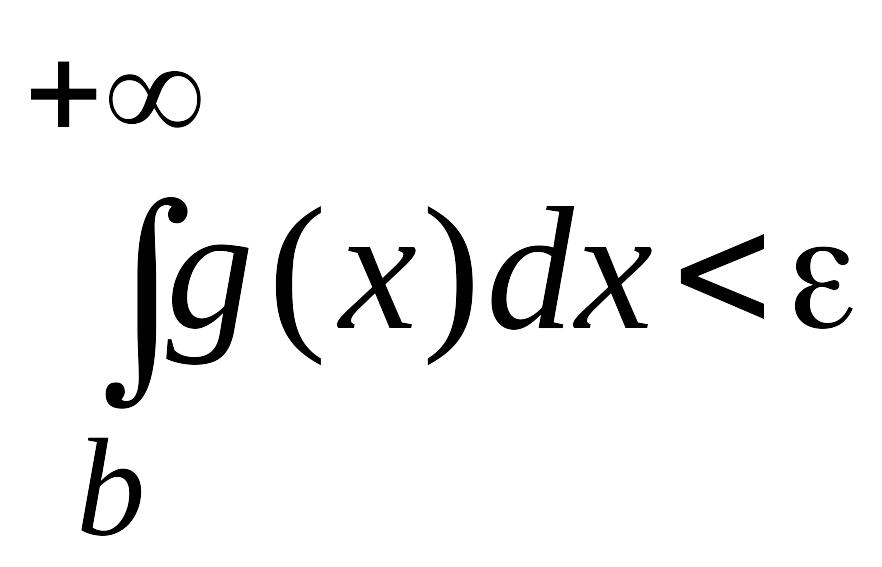. В силу (30) имеем

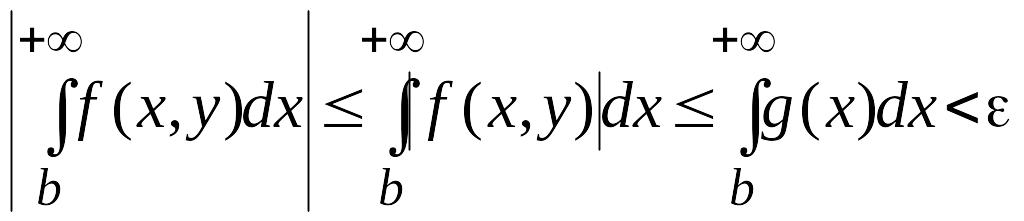для и .

Следовательно, несобственный интеграл (29) сходится равномерно на . <

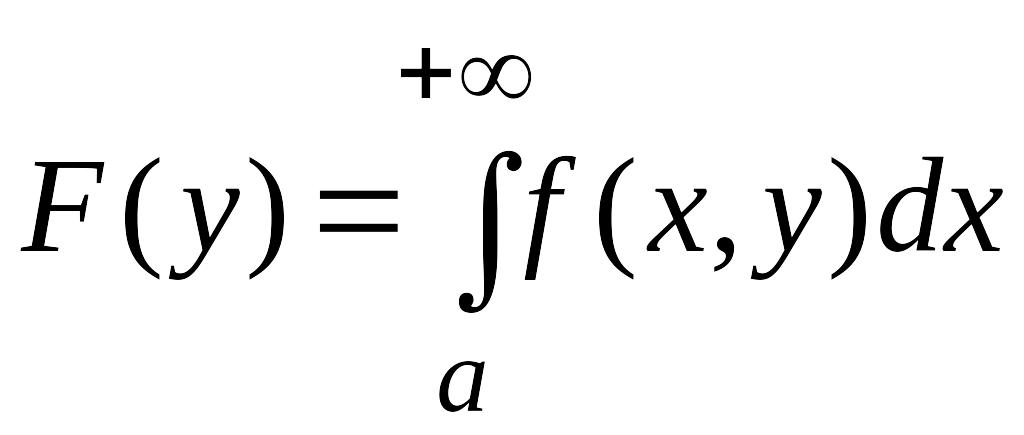Теорема 18. Пусть функция непрерывна на множестве и интеграл (29) сходится равномерно на . Тогда функция непрерывна на .

‰ Пусть - произвольная точка , т.е. . Тогда

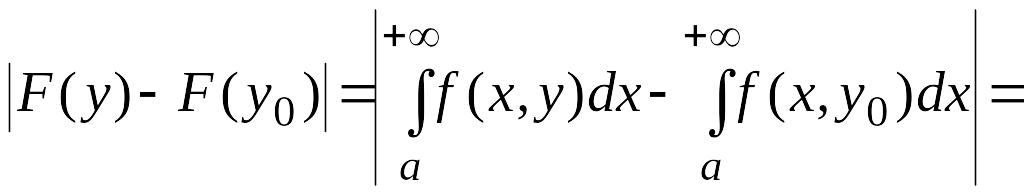
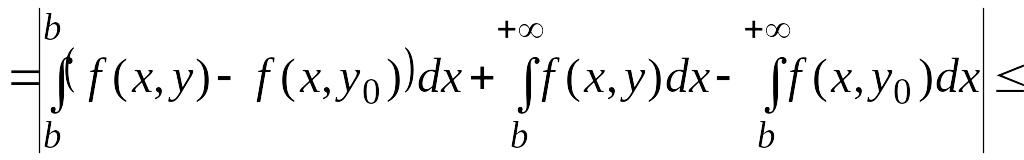
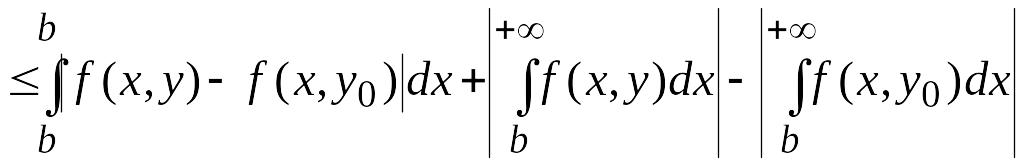. (31)

В силу равномерной сходимости несобственного интеграла (29) для такое, что для

,

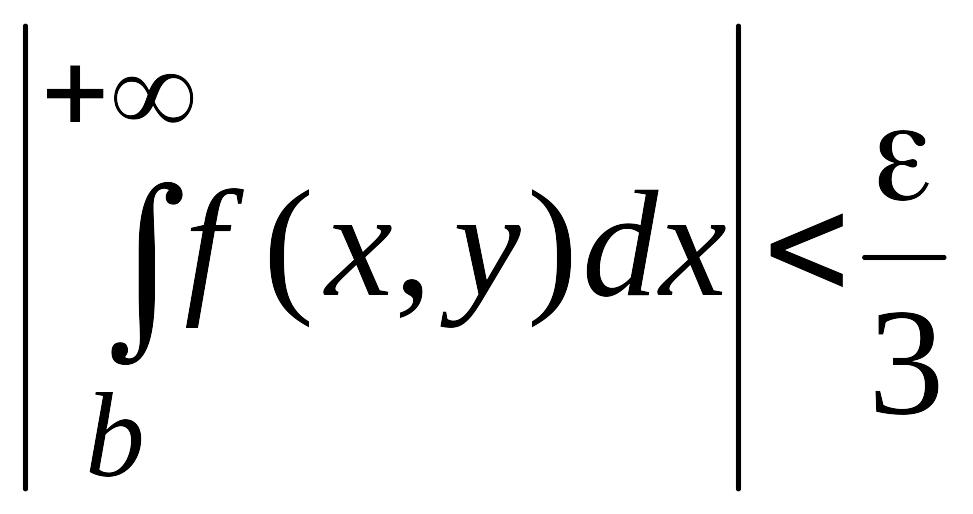тогда

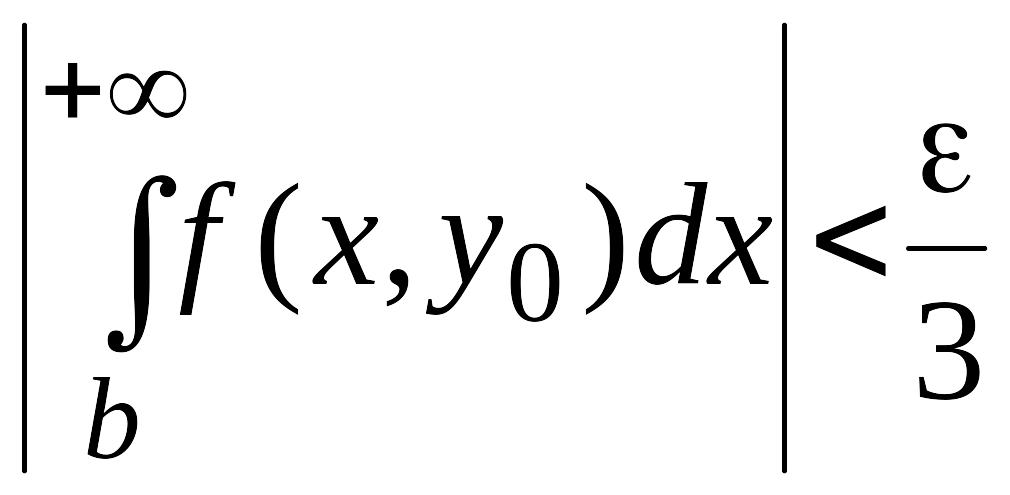. (32)

Фиксируем некоторое . Функция непрерывна на прямоугольнике , следовательно, по теореме Кантора она равномерно непрерывна на П, т.е. такое, что для выполняется . Отсюда следует, что

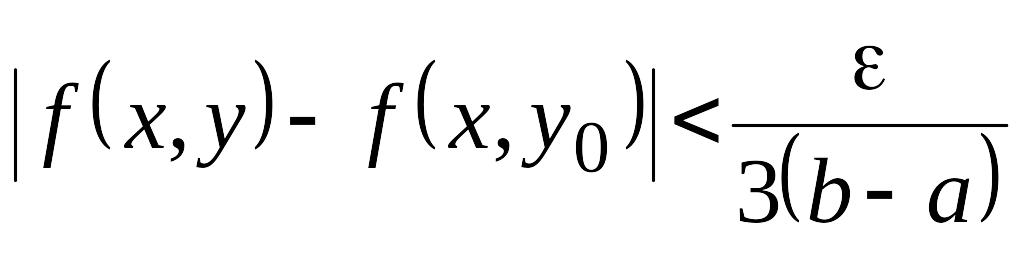. (33)

Из (31), (32), (33) следует, что

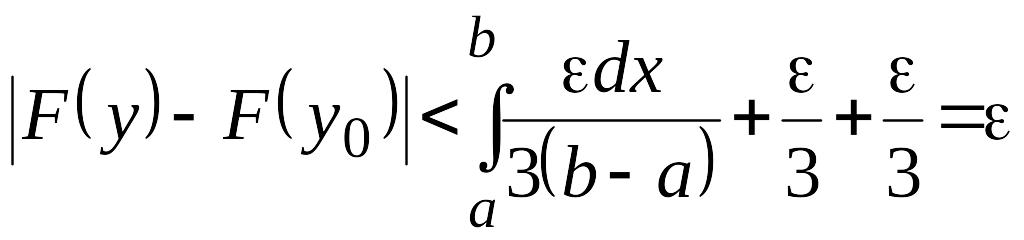, при .

Следовательно, непрерывна в произвольной точке. ■

Теорема 19. Пусть непрерывна на множестве и интеграл (29) сходится равномерно на . Тогда

.

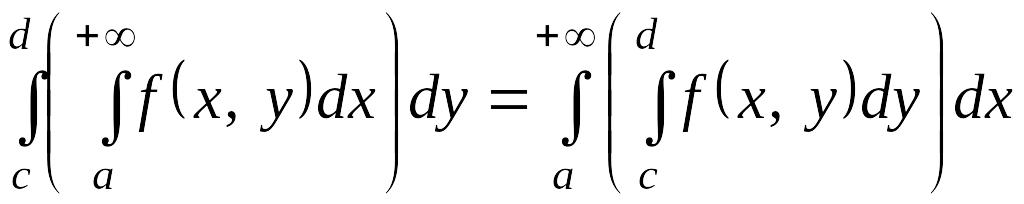ÿ Пусть , тогда в силу следствия к теореме 15 имеем

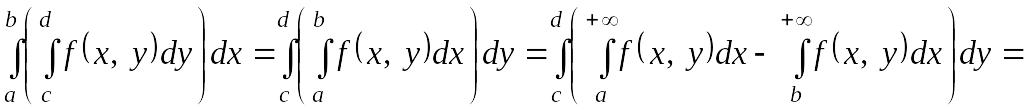
. (34)

Из равномерной сходимости интеграла (29) следует, что для , что при и получаем

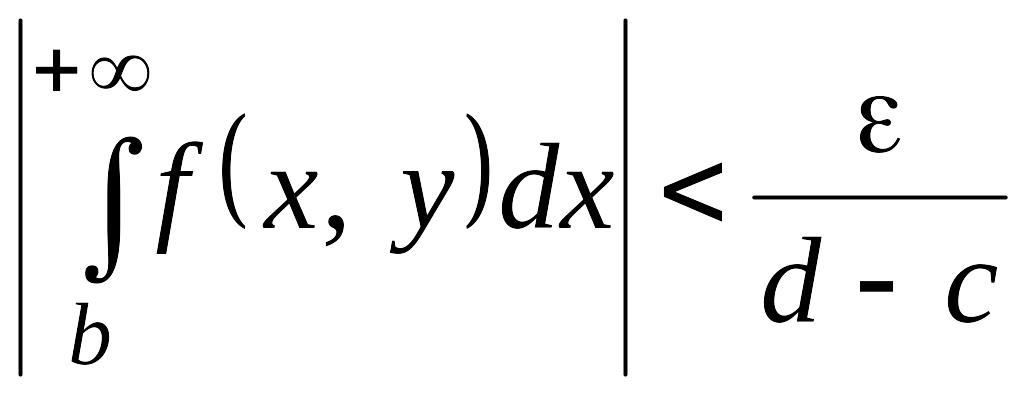
и тогда

.

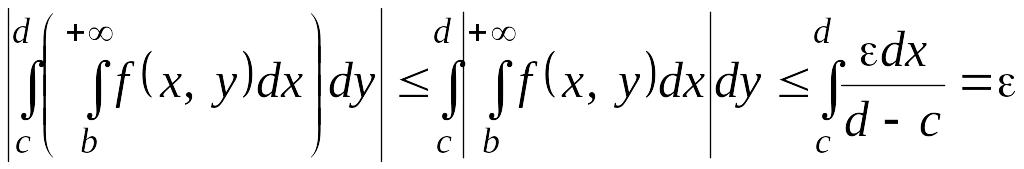Следовательно,

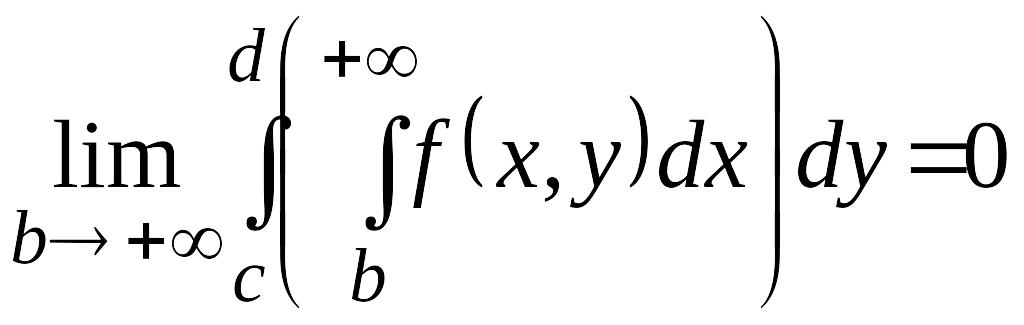. (35)

Переходя в равенстве (34) к пределу при , в силу (35) получим:

. <

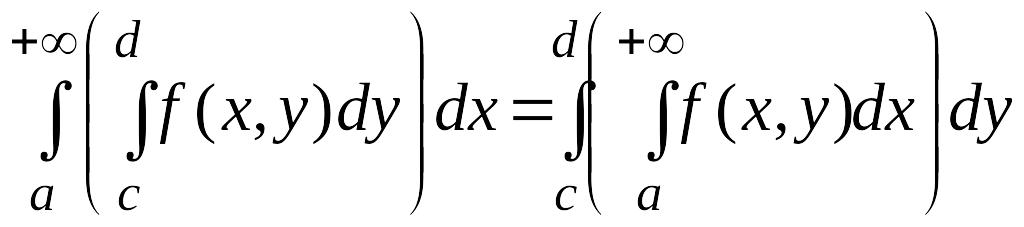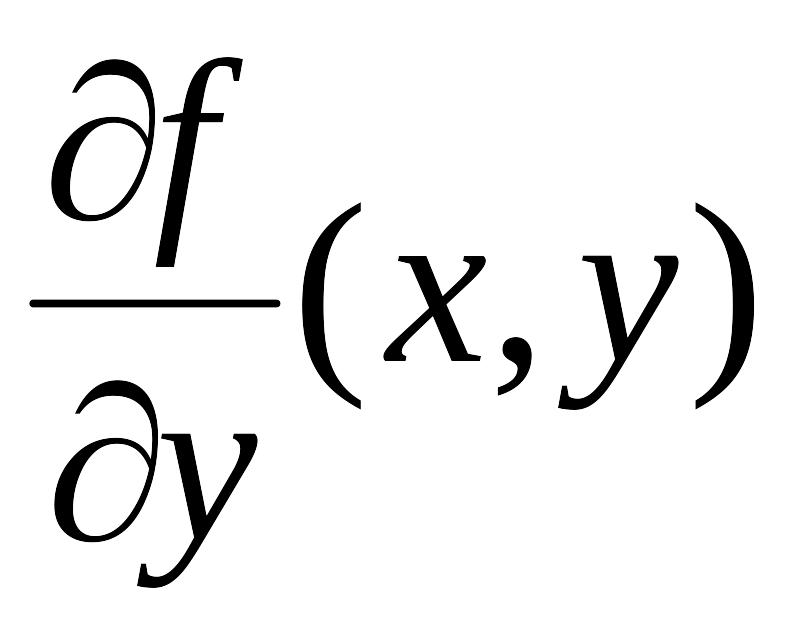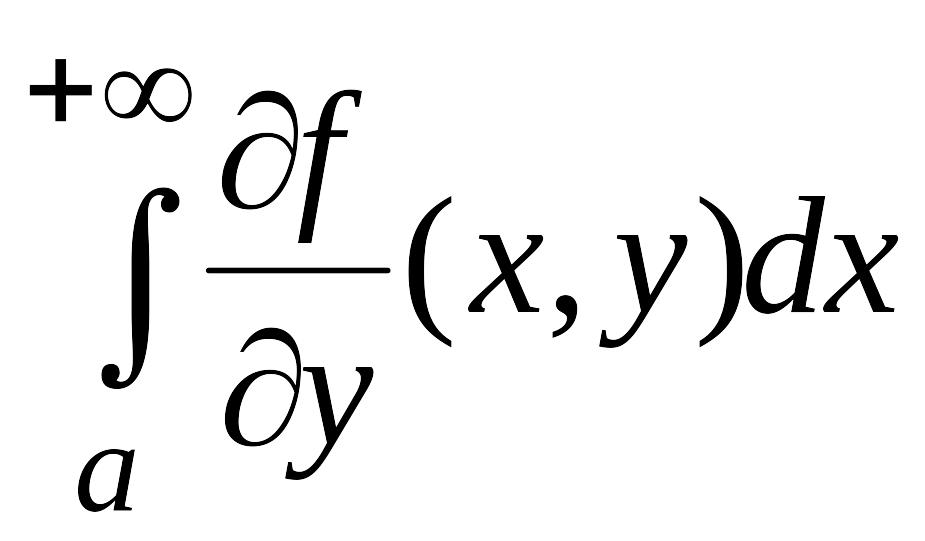Теорема 20. Пусть функция , частная производная и интеграл (29) непрерывны на , а интеграл - сходится равномерно на . Тогда функция непрерывно дифференцируема на и справедлива формула: .

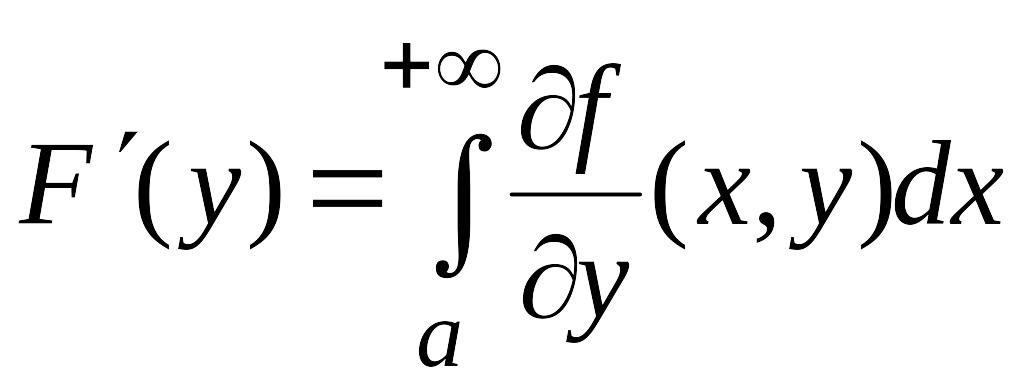□ Пусть 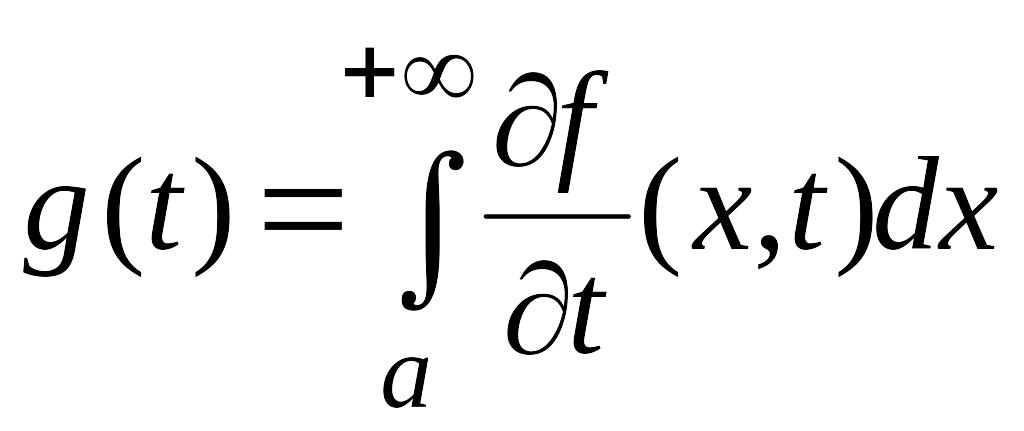, . В силу теоремы 19, имеем

.

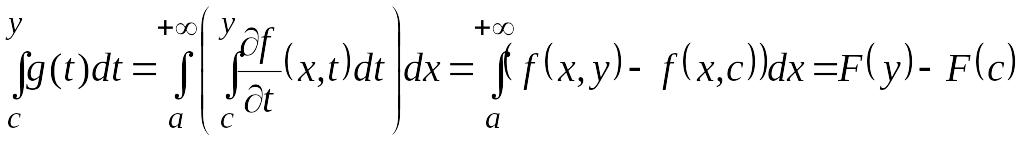Таким образом, 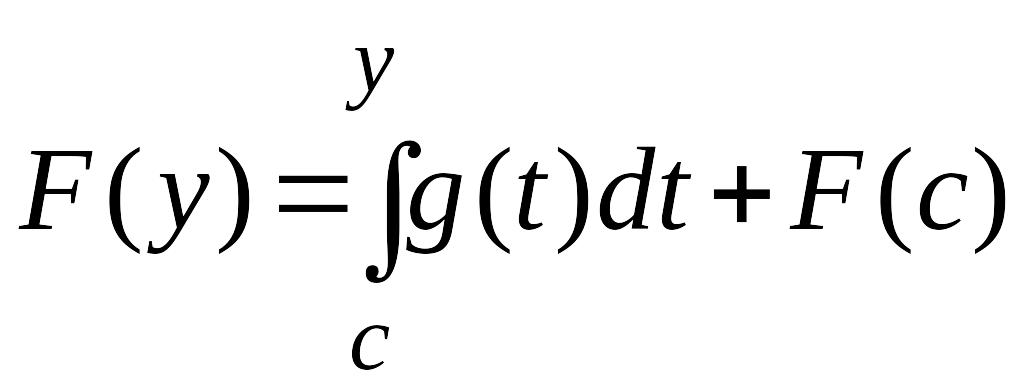. Отсюда следует, что

.

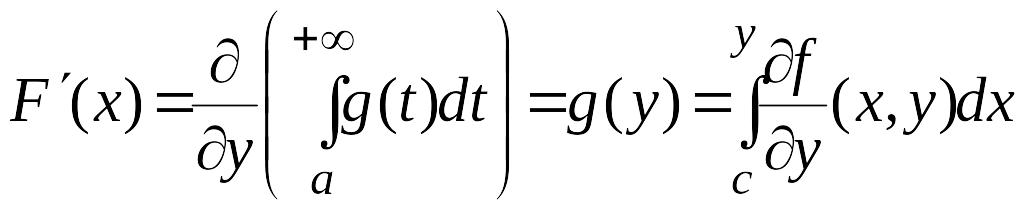В силу теоремы 18, производная непрерывна на . <

Пример 16. Вычислить , .

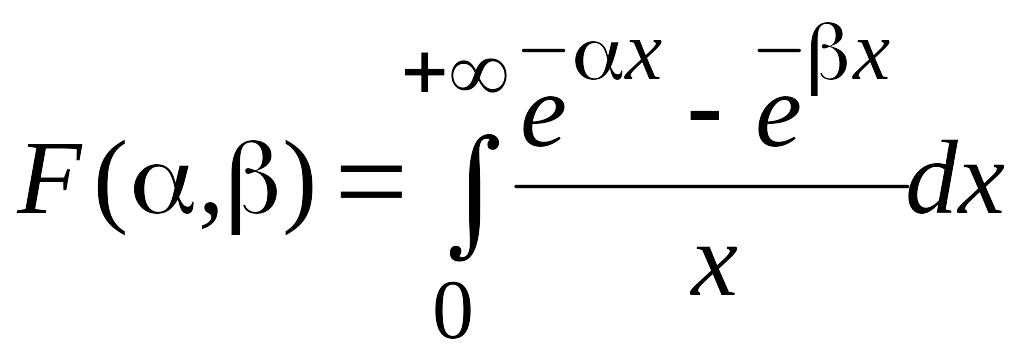Решение. Будем считать b - фиксированной величиной, а a - параметром. Обозначим , тогда . Легко проверить, что интеграл сходится для . Пусть , .

Интеграл 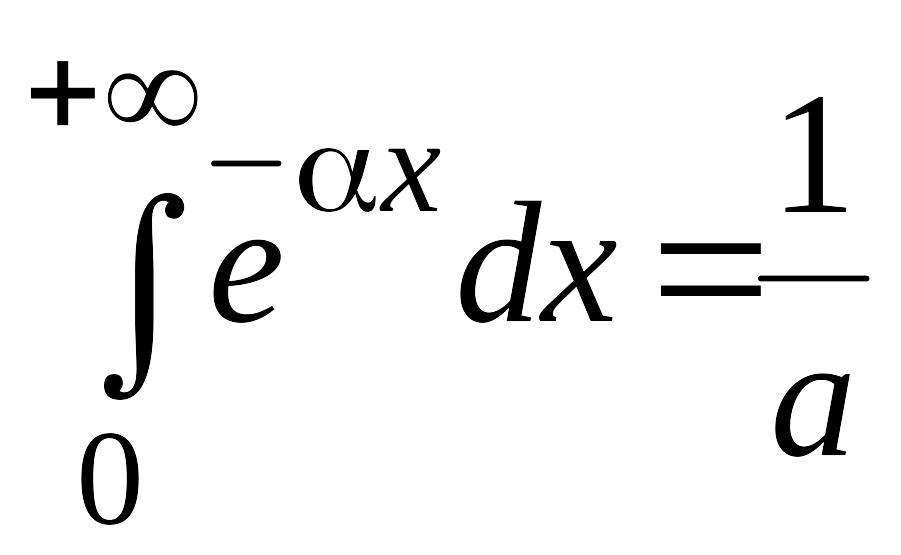, т.е. сходится. Тогда по признаку Вейерштрасса следует равномерная сходимость по параметру a интеграла 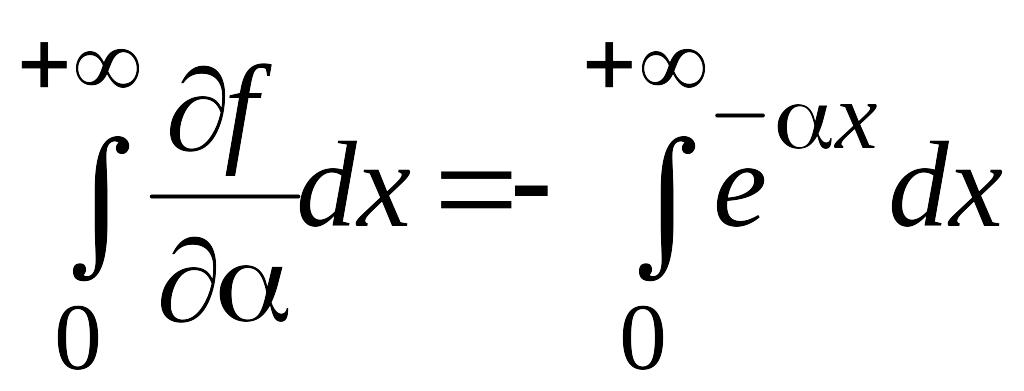на отрезке . В этом случае несобственный интеграл можно дифференцировать по параметру под знаком интеграла

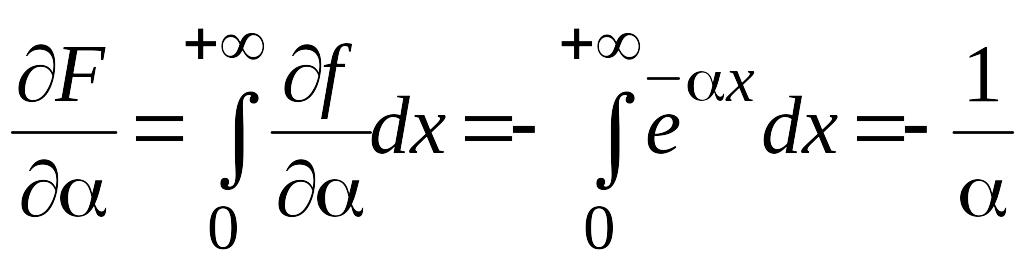при .

Тогда 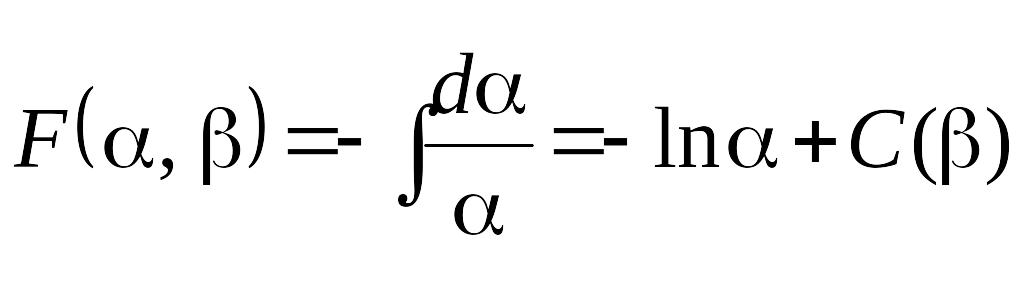. Так как , то . Таким образом, получаем

.
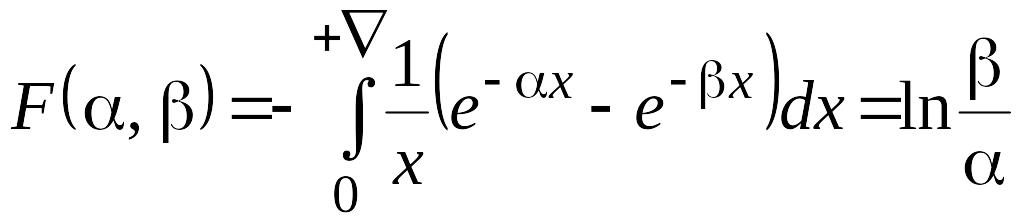