
- •Глава 8. Неявные функции. Дифференцируемые Отображения
- •8.1. Неявные функции заданные одним уравнением
- •8.2. Векторные отображения
- •В силу (13) это будет означать, что
- •Предел отображения обозначается:
- •8.3. Неявные функции n-переменных. Обратные отображения
- •8.4. Условный экстремум
- •8.5. Поверхности в трехмерном евклидовом пространстве
- •8.6. Контрольные вопросы
- •8.7. Примеры решения задач
- •8.8. Задачи для самостоятельного решения
8.3. Неявные функции n-переменных. Обратные отображения
Пусть
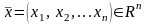 и задано уравнение
и задано уравнение
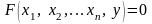 (21)
(21)
или
в векторном виде
 .
.
Функцию
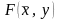 будем предполагать заданной в цилиндре
будем предполагать заданной в цилиндре
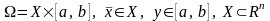 .
.
Если
существует функция
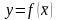 ,
определенная на множестве
,
такая, что
,
определенная на множестве
,
такая, что
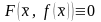 ,
при
,
то говорят, что
неявная функция, заданная уравнением
(21).
,
при
,
то говорят, что
неявная функция, заданная уравнением
(21).
Имеют место следующие теоремы, которые оставим без доказательства.
Теорема
8.7. Пусть
выполняются следующие условия:
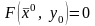 ;
дифференцируема в
;
дифференцируема в
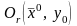 ;
;
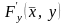 непрерывна в
;
непрерывна в
;
 .
Тогда найдутся
.
Тогда найдутся
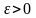 и
и
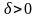 ,
что в некоторой окрестности точки
,
что в некоторой окрестности точки
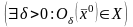 уравнение (21) имеет единственное решение
удовлетворяющее условию
уравнение (21) имеет единственное решение
удовлетворяющее условию
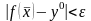 ,
причем
дифференцируема и справедливы формулы:
,
причем
дифференцируема и справедливы формулы:
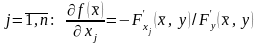 .
(22)
.
(22)
Пример
10. Найти в
точке
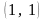 частные производные функции
частные производные функции
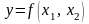 ,
заданной уравнением
,
заданной уравнением
 .
.
Решение.
Из уравнения найдем значение функции
в данной точке
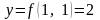 .
.
Функция
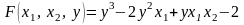 равна 0 в точке (1, 1, 2) и непрерывна в ее
окрестности. Функции
равна 0 в точке (1, 1, 2) и непрерывна в ее
окрестности. Функции
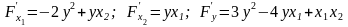
непрерывны,
причем
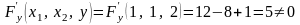 .
Следовательно, данное уравнение в
окрестности точки (1, 1, 2)
.
Следовательно, данное уравнение в
окрестности точки (1, 1, 2)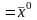 определяет единственную непрерывно
дифференцируемую функцию
определяет единственную непрерывно
дифференцируемую функцию
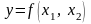 ,
частные производные которой можно найти
по формулам (22):
,
частные производные которой можно найти
по формулам (22):
 ,
,
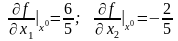 .
.
Рассмотрим систему уравнений
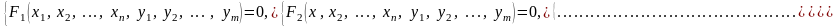
или
в векторном виде:
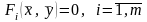 ,
(23)
,
(23)
где
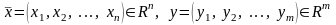 .
.
Пусть
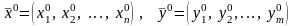 – фиксированные точки.
– фиксированные точки.
Теорема
8.8. (о
существовании решении системы неявных
функций). Пусть выполняются условия
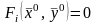 ;
функция
;
функция
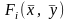 дифференцируема в окрестности точки
дифференцируема в окрестности точки
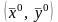 ;
частная производная
;
частная производная
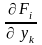 непрерывна в
непрерывна в
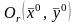 ;
;
 .
Тогда существуют
и
такие, что для
.
Тогда существуют
и
такие, что для
 система уравнений
система уравнений
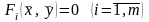 имеет единственное решение:
имеет единственное решение:
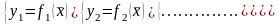 .
удовлетворяют условиям
.
удовлетворяют условиям
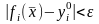 ,
при этом функции
,
при этом функции
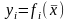 – дифференцируемы.
– дифференцируемы.
Замечание.
Если в теоремах 8.7 и 8.8 потребовать также
непрерывность частных производных
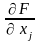 и
и
 в
в
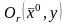 и
и
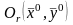 ,
то производные
,
то производные
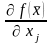 и
и
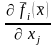 будут непрерывными.
будут непрерывными.
Пусть
отображение открытого множества
в
,
т.е.
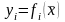 ,
,
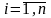
 .
.
Если
отображение взаимно однозначное, то
существует обратное отображение
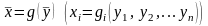 ,
которое отображает множество
,
которое отображает множество
 – значений функции
на множество
.
При этом имеет место тождество
– значений функции
на множество
.
При этом имеет место тождество
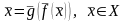 ,
,
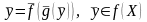
или в координатной форме
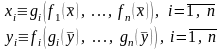 (24)
(24)
Определение
9. Отображение
называется непрерывно
дифференцируемым на открытом множестве
,
если частные производные
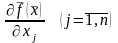 – непрерывны на множестве
.
– непрерывны на множестве
.
Теорема
8.9. Пусть
взаимно-однозначное и непрерывно-дифференцируемое
отображение открытого множества
на открытое множество
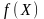 ,
причем обратное отображение
,
причем обратное отображение
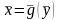 также непрерывное и дифференцируемое.
Тогда якобианы этих отображений отличны
от нуля и имеют место равенства:
также непрерывное и дифференцируемое.
Тогда якобианы этих отображений отличны
от нуля и имеют место равенства:
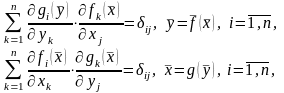 (25)
(25)
и для якобианов выполняются:
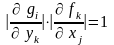 или
или
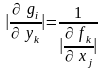 .
(26)
.
(26)
Равенства
(25) получаются дифференцированием
тождеств (24) по
и
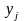 соответственно, если используется
правило дифференцирования сложной
функции. Так как
соответственно, если используется
правило дифференцирования сложной
функции. Так как
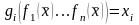 ,
то
,
то
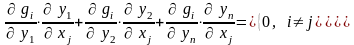 ,
,
тогда
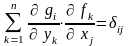 .
.
Аналогично получают второе равенство из (25). Для доказательства (26) запишем первое равенство из (25) в матричной форме
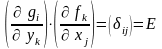 . (27)
. (27)
Известно, что определитель произведения двух матриц равен произведению определителей этих матриц. Тогда из (27) получается (26), откуда следует, что якобианы отображений не равны нулю.
Для функций одной переменной имеется простое достаточное условие обратимости дифференцируемой функции на промежутке, т.е. условия существования обратной функции. Этим условием является неравенство ее производной нулю. Но уже для случая функции двух переменных аналогичного простого признака существование обратного отображения нет. Однако имеете место условие локальной обратимости отображения в достаточно малой окрестности точки.
Теорема
8.10. Пусть
непрерывно дифференцируемое отображение
открытого множества
,
причем якобиан
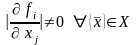 .
Тогда для
существует такая окрестность
.
Тогда для
существует такая окрестность
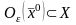 ,
в которой отображение
взаимно-однозначное, причем обратное
отображение
непрерывно дифференцируемо и его якобиан
не равен нулю.
,
в которой отображение
взаимно-однозначное, причем обратное
отображение
непрерывно дифференцируемо и его якобиан
не равен нулю.
Пусть
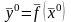 ,
.
,
.
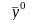 – произвольная точка множества
– произвольная точка множества
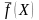 .
В силу теоремы о существовании системы
функций для достаточно малых
и
.
В силу теоремы о существовании системы
функций для достаточно малых
и
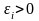 и произвольной точки
и произвольной точки
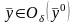 существует единственное решение
уравнения
,
удовлетворяющее условиям
существует единственное решение
уравнения
,
удовлетворяющее условиям
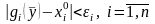 .
.
При этом,
в силу замечания к теореме 8.8 функция
непрерывно дифференцируема в
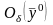 .
А отсюда вытекает, что отображение
взаимно-однозначное в некоторой
окрестности
.
А отсюда вытекает, что отображение
взаимно-однозначное в некоторой
окрестности
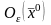 ,
,
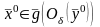 ,
а, следовательно, по теореме 8.9 обратное
отображение непрерывно дифференцируемо
и его якобиан не равен нулю.
,
а, следовательно, по теореме 8.9 обратное
отображение непрерывно дифференцируемо
и его якобиан не равен нулю.
Пример 11. Рассмотрим
отображение
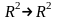 ,
т.е.
,
т.е.
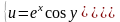 .
.
Решение. Якобиан:
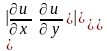 ,
для любой точки
,
для любой точки
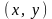 .
Это отображение не является
взаимно-однозначным на плоскости.
Например, точки
.
Это отображение не является
взаимно-однозначным на плоскости.
Например, точки
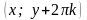 ,
,
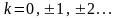 переходят при этом отображении в одну
и ту же точку
переходят при этом отображении в одну
и ту же точку
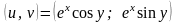 .
Тем не менее, в силу теоремы 8.9. это
отображение взаимно однозначное в
достаточно малой окрестности любой
точки
.
Тем не менее, в силу теоремы 8.9. это
отображение взаимно однозначное в
достаточно малой окрестности любой
точки
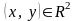 .
.
