
- •Х.Г. Акопянц теория линейных электрических цепей
- •Часть I
- •Учебное пособие.
- •Часть 1.
- •Рассмотрим в качестве отклика ток, протекающий в заданной цепи (рис. 1.1):
- •Отклик линейной цепи на суммарное воздействие равен сумме откликов этой же цепи на каждом из слагаемых воздействий в отдельности.
- •3. Схемные функции электрических цепей
- •В общем виде, функции цепи выражаются следующими соотношениями:
- •Вычислить переходную характеристику для схемы (рис. 3.16)-дифференцирующая цепь.
- •4. Временные методы анализа линейных цепей
- •Перепишем (4.1) в виде:
- •В этом случае сигнал s(t) может быть представлен в виде:
- •6. Теорема котельникова
- •В самом деле, легко показать(*), что
- •Погрешность восстановления сигнала определяется следующими факторами,
6. Теорема котельникова
В технике цифровой обработки аналоговый сигнал подвергается дискретизации. В этой связи существенным является вопрос об интервале дискретизации сигналов различной формы.
Ответом на заданный вопрос является теорема Котельникова, которая формулируется следующим образом:
Непрерывная
функция времени
со спектром, ограниченным
,
может быть полностью представлена
отсчетами с интервалом
![]() (или
(или
![]() ).
).
Соотношение называют постоянной Котельникова.
Доказательство теоремы базируется на теории обобщенных рядов Фурье.
Запишем представление в виде обобщенного ряда Фурье:
![]() (6.1)
(6.1)
Выберем в качестве базисной функции
![]() ,
,
где - интервал дискретизации;
- верхняя частота спектра функции ;
- числа натурального ряда: 0, 1, 2... и представим в виде ряда
![]() .
(6.2)
.
(6.2)
Здесь
![]() -
выборка функции
в точке
-
выборка функции
в точке
![]() .
Покажем, что ряд (6.2) является обобщенным
рядом Фурье, т.е.
.
Покажем, что ряд (6.2) является обобщенным
рядом Фурье, т.е.
![]() - ортогональная функция, а
являются коэффициентами обобщенного
ряда Фурье.
- ортогональная функция, а
являются коэффициентами обобщенного
ряда Фурье.
Проверим
ортогональность
![]()
В самом деле, легко показать(*), что
![]() при
при
![]()
и,
таким образом
![]() .
.
Покажем,
что
- выборки функции
являются коэффициентами обобщенного
ряда Фурье
![]() .
.
Формула
обратного преобразования Фурье дает
значение функции
в любой заданной точке, например, в точке
![]() .
.
![]() (6.3)
(6.3)
![]() -Градштейн
И.С., Рыжик И.М. Таблицы интегралов, сумм,
рядов и произведений. М.: Ф.-М., 1963.
-Градштейн
И.С., Рыжик И.М. Таблицы интегралов, сумм,
рядов и произведений. М.: Ф.-М., 1963.
Учитывая,
что спектр
согласно определению ограничен
![]() и подставляя в (6.3) значение
,
получим
и подставляя в (6.3) значение
,
получим
![]() .
(6.4)
.
(6.4)
Изменим порядок интегрирования в (6.4):
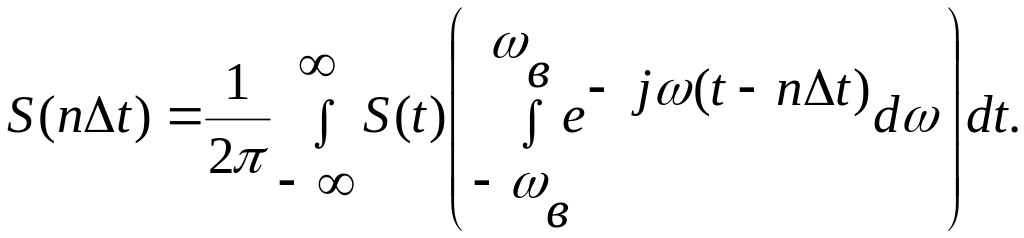 (6.5)
(6.5)
Рассмотрим внутренний интеграл в (6.5):
![]() (6.6)
(6.6)
Подставляя (6.6) в (6.5), получаем окончательно:
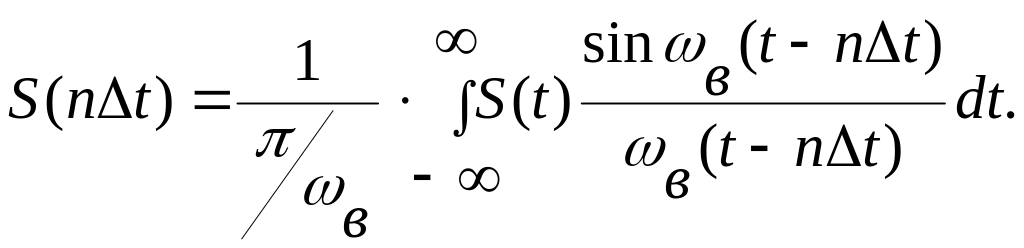 (6.7)
(6.7)
Напомним,
что
![]()
Таким
образом,
являются коэффициентами обобщенного
ряда Фурье при разложении
в базисе
![]() и мы можем представить функцию
со спектром, ограниченным
в, виде ряда Фурье:
и мы можем представить функцию
со спектром, ограниченным
в, виде ряда Фурье:
![]() (6.8)
(6.8)
Множество
является спектром функции
и
однозначно ее характеризует,
следовательно, по известному множеству
![]() можно восстановить функцию
.
можно восстановить функцию
.
Восстановление аналоговой функции по ее отсчетам (выборкам).
Пусть
сигнал
со спектром, ограниченным
,
подвергается дискретизации с
интервалом
![]() (рис.6.1).
(рис.6.1).
Исходная непрерывная функция показана пунктиром.
Функцию можно восстановить с достаточной степенью точности.
Рис.6.1
Просуммируем члены ряда (6.8).
Обозначим
восстановленную функцию
![]() :
:
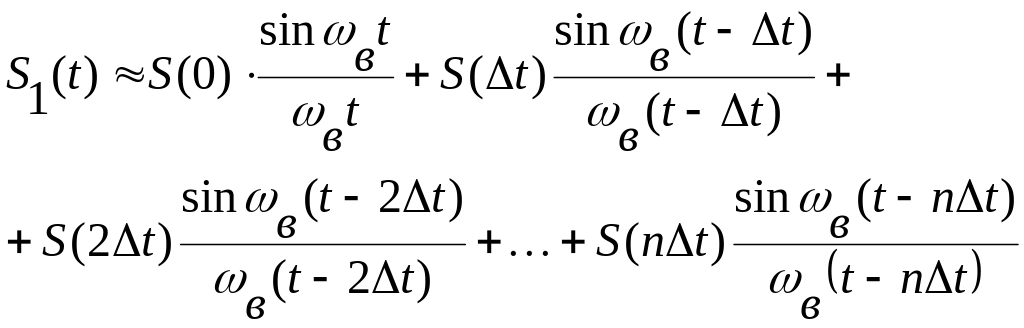 (6.9)
(6.9)
Функция
![]() в точках
в точках
![]() равна 1,
равна 1,
в
точках кратных
![]() и т.д. обращается в 0. Таким образом
,
отображенная рядом (6.9) имеет вид
(рис.6.2).
и т.д. обращается в 0. Таким образом
,
отображенная рядом (6.9) имеет вид
(рис.6.2).
Рис. 6.2
6.1 Аппаратурная реализация процесса дискретизации сигнала и его последующего восстановления по отсчетам
Принцип действия системы дискретизация - восстановление поясняется на рис.6.3.
1.Электронный
ключ, замыкающий цепь с интервалом
![]() .
2. Фильтр
нижних частот (ФНЧ).
.
2. Фильтр
нижних частот (ФНЧ).
- исходный сигнал, подвергаемый дискретизации.
- выборки.
- восстановленный сигнал.

Рис. 6.3
Электронный
ключ 1 производит выборки сигнала
в моменты
![]() ,
и на выходе его получаем последовательность
импульсов с амплитудой
и длительностью
,
и на выходе его получаем последовательность
импульсов с амплитудой
и длительностью
![]() ,
которые подаются на приемном конце
линии на ФНЧ. С выхода ФНЧ получаем
последовательность сигналов вида
,
которые подаются на приемном конце
линии на ФНЧ. С выхода ФНЧ получаем
последовательность сигналов вида
![]() ,
(6.10)
,
(6.10)
которые
суммируются со сдвигом во времени
![]() и образуют восстановленный сигнал
.
и образуют восстановленный сигнал
.
Р ис.
6.4
ис.
6.4
Рассмотрим механизм образования на выходе ФНЧ сигнала вида (6.10). Полагая ФНЧ идеальным, зададим его характеристики следующим образом:
![]() ;
;
![]()
граничная
частота фильтра
![]() ;
;
- наклон фазовой характеристики фильтра, определяющий время прохождения сигнала через фильтр (время запаздывания).
Определим импульсную характеристику фильтра с заданными параметрами:
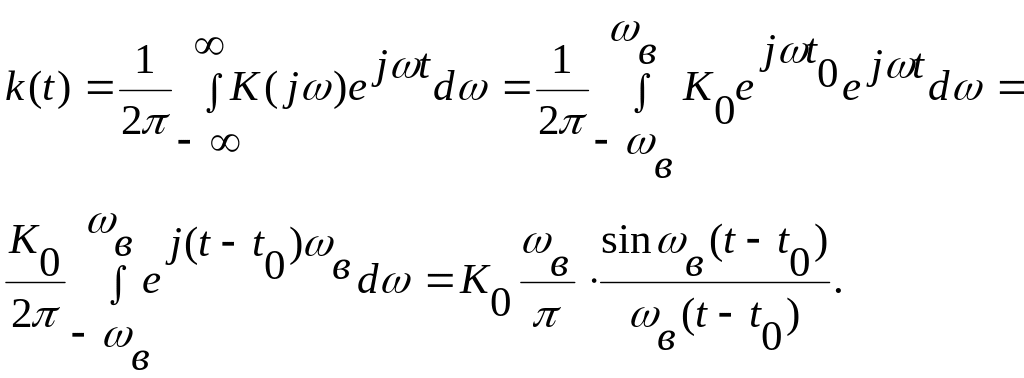
Зададим
![]()
В этом случае импульсная характеристика ФНЧ будет равна
![]() ,
,
а в момент соответственно:
![]() (6.11)
(6.11)
Таким образом, отклик идеального ФНЧ с заданными выше параметрами на воздействие импульса с амплитудой будет равен
![]()
а это и есть член ряда Котельникова.
