Перепишем (4.1) в виде:

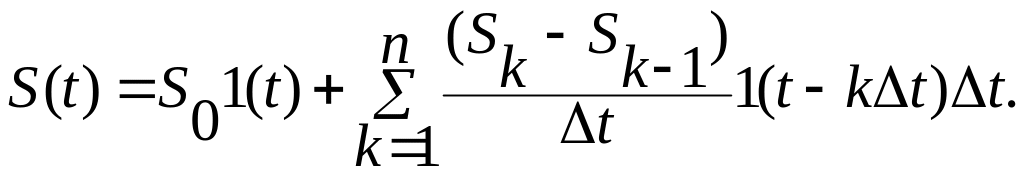(4.2)

Для повышения точности представления S(t) уменьшим интервалы до бесконечно малой величины dt, соответственно дискретная переменная замещается непрерывной . Учитывая, что

, (4.3)

сумму (4.2) заменяем интегралом вида:

(4.4)

Соотношение (4.4) является формой динамического представления сложного сигнала в виде суперпозиции элементарных сигналовнеединичных скачков.

4.1.2. Представление сигнала в виде суперпозиции неединичных импульсов

Сложный сигнал может быть также представлен в виде суперпозиции элементарных импульсов длительностью (рис. 4.2).

Рис. 4.2

элементарный импульс с амплитудой :

; (4.5)

Представим kый импульс как разность неединичных скачков с амплитудой :

Умножив и разделив (4.5) на , получаем:

.

Тогда сигнал S(t) можно записать в виде суммы:

. (4.6)

Для увеличения точности представления сигнала уменьшаем длительность элементарных импульсов до бесконечно малой величины dt , дискретную переменную заменяем непрерывной переменной .

Учитывая, что ,

сумму (4.6) заменяем интегралом вида:

(4.7)

Соотношение (4.7) является формой представления сложного сиг­нала в виде суперпозиции элементарных сигнловнеединичных им­пульсов.

4.2.Метод интеграла Дюамеля

Метод позволяет получить отклик цепи, заданной переходной функцией h(t) на воздействие сложного входно­го сигнала (рис. 4.3).

Рис. 4.3

Для получения отклика воспользуемся промежуточным соотношением (4.2) динамического представления входного сигнала в виде суперпо­зиции неединичных скачков. Учитывая, что откликом цепи на воздей­ствие единичного скачка является переходная функция цепи, представляем в виде:

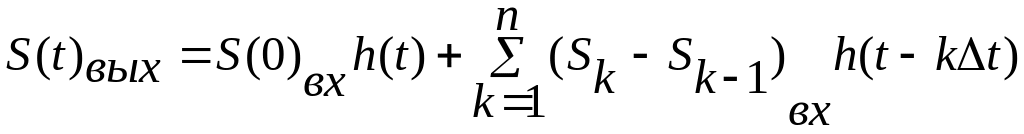, (4.9)

далее, уменьшая до бесконечно малой величины dt и заме­няя дискретную переменную на непрерывную , преобразуем сумму (4.9) в интеграл:

(4.10)

Соотношение (4.10) является одной из форм интеграла Дюамеля и позволяет найти отклик цепи на заданный сигнал , если известна переходная характеристика цепи.

Проводя для (4.10) интегрирование по частям, имеем:

,

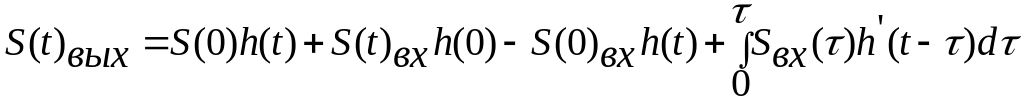и окончательно

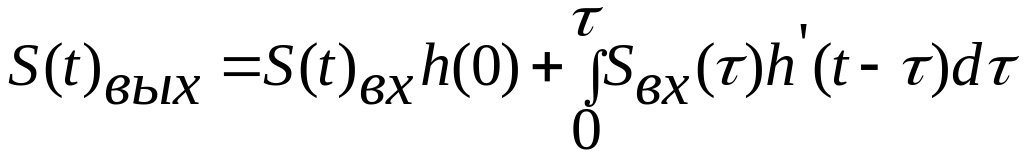. (4.11)

Это вторая форма интеграла Дюамеля.

Выбор формы (4.10) или (14.11) производится исходя из удобства вычислений.

ПРИМЕР 4.1

Определить отклик цепи (рис. 4.4) на заданный сигнал.

Переходная функция цепи

.

Входной сигнал

.

Рис. 4.4

Используем вторую форму интеграла Дюамеля.

Обозчив,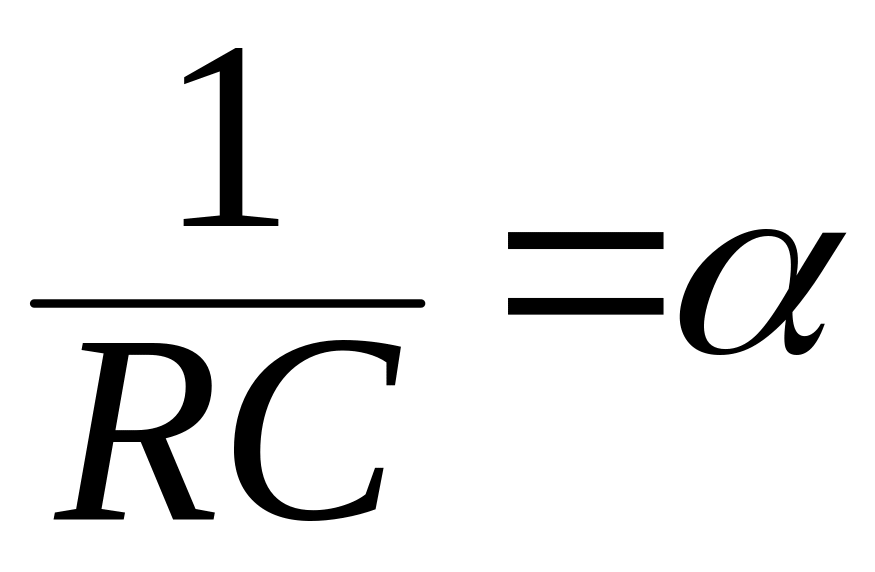 , имеем: .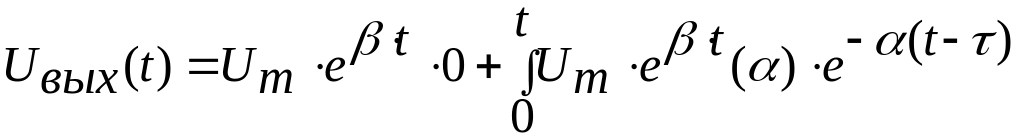

В результате получаем:

.

ПРИМЕР 4.2

На вход схемы (рис. 4.5) подается линейно растущее напряжение: ,переходная функция цепи .

Найдем методом интеграла Дюамеля.

В данном случае имеет смысл выбрать первую форму, так как за счет дифференцирования упрощается под интегральное выра­жение:

Рис. 4.5

.

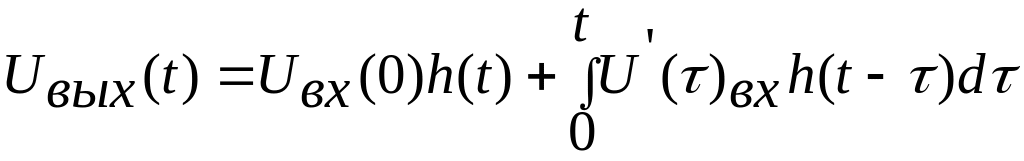Подставим данные:

.

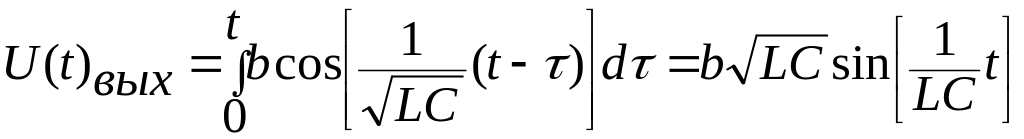Обозначив 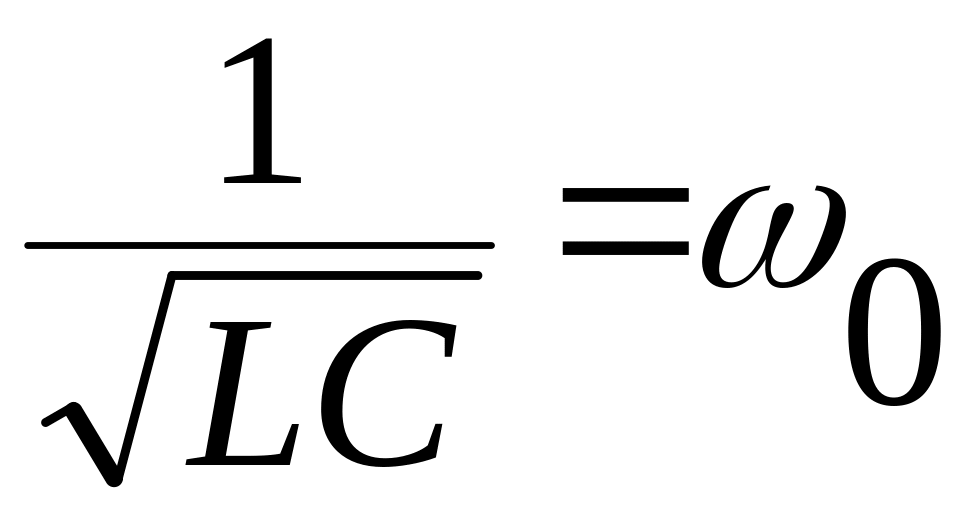, окончательно получим:

.

При воздействии на вход цепи сигналов сложной, с точки зрения аналитической записи, формы их можно представить в виде суммы бо­лее простых выражений.

ПРИМЕР 4.3

Н а вход цепи с подается симметричный треугольный импульс длительностью и высотой Е (см. рис. 4.6). Найти форму напряжения на выходе цепи методом интеграла Дюамеля.

Введем обозначения:

,

Рис. 4.6

Запишем в виде суммы трех напряжений (рис. 4.7):

1.

2.

3.

Рис. 4.7

Итак,

Далее, применяя первую форму интеграла Дюамеля и каждому из слага­емых входного напряжения, получаем для первого слагаемого:

,

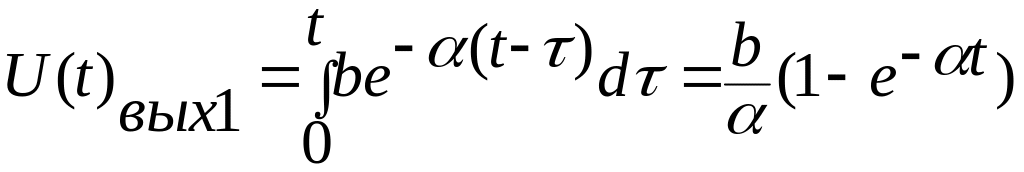аналогично с учетом сдвига на и - 2 и 3 слагаемых получаем окончательно:

4.2.1.Особенность использования интеграла Дюамеля для анализа отклика цепи на скачкообразный сигнал, имеющий различную форму в отдельные интервалы времени

Сигнал вида (см. рис.4.8) претерпевает скачки в точках: t=0, ;

-функции различного вида.

Для анализа отклика методом интеграла Дюамеля данный сигнал разбивается на интервалы между скачками, и отклик вычисляется для каждого интервала отдельно, при этом:

- на каждом временном интервале учитывается только левый

ска­чок;

- а правый в следующем за ним интервале.

Для данного сигнала :

1. Интервал 0  ;

2. Интервал ;

3. Интервал .

Итак,

1.Интервал

.

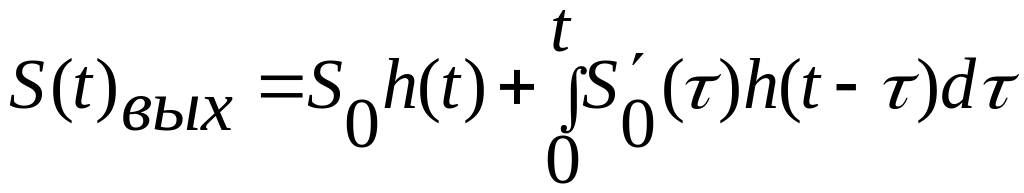2. Интервал

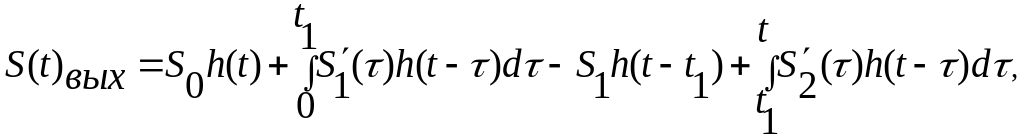
3.Интервал

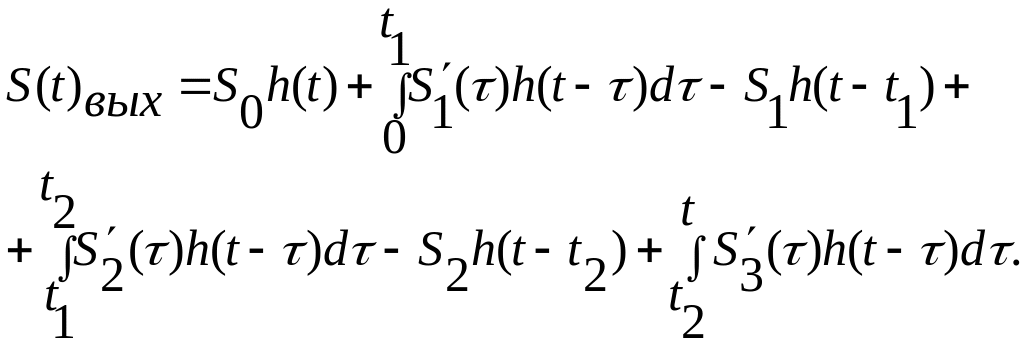
График функции строится в рамках указанных выше интервалов.

4.3. Метод импульсных функций

Метод импульсные функций рассматривается как модификация мето­да интеграла Дюамеля и также позволяет получить отклик цепи, заданной импульсной функцией, на воздействие входного сигнала .

Воспользуемся динамическим представлением сигнала в виде суперпозиции элементарных импульсов.

Вернемся к приближенному представлению(4.5) :

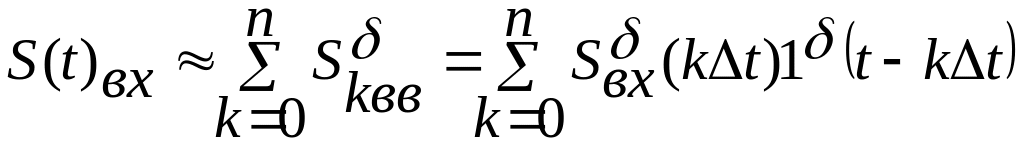
Как было показано выше:

,

и далее уменьшая до бесконечно малой величины , и

заменяя дискретную переменную непрерывной , получим выражение единичного импульса в виде:

.

Элементарный импульс воздействия в момент t= равен

. (4.12)

Учитывая, что отклик цепи на воздействие равен импульс­ной характеристике цепи, запишем элементарный импульс отклика в виде:

. (4.13) Интегрируя (4.13) в пределах 0t получаем функцию откли­ка на выходе:

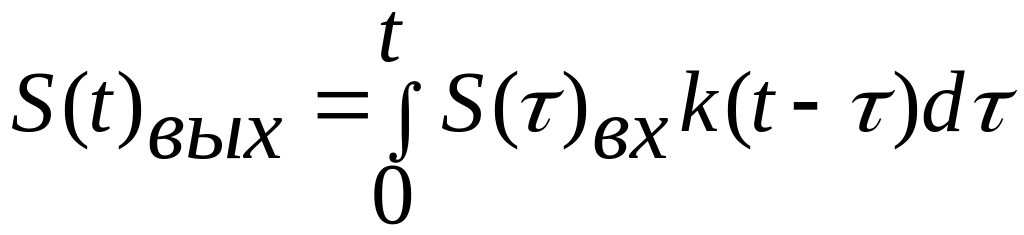. (4.14)

Это выражение является формулой метода импульсных функций.

ПРИМЕР 4.4

Определить отклик цепи (рис. 4.9) на заданный сигнал

. Импульсная функция цепи: .

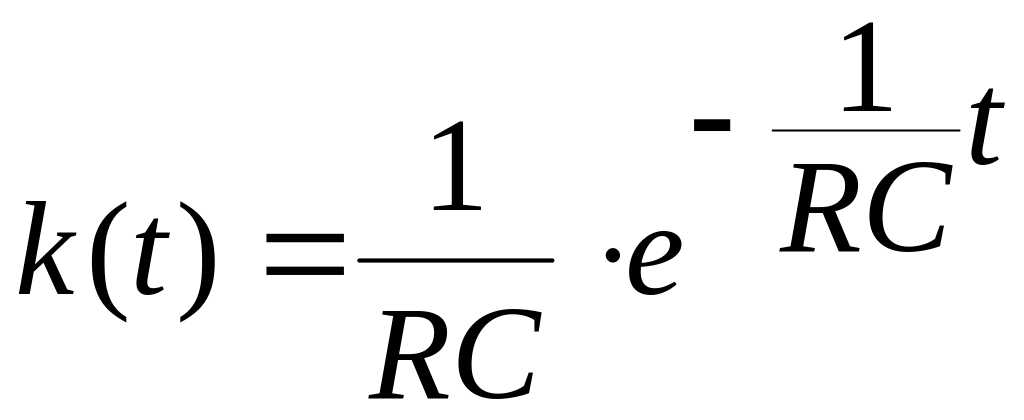О бозначив , запишем отклик в виде:

Рис.4.9

В результате:

.

4.3.1.Особенности применения метода импульсных функций

для сигналов скачкообразной формы

Пусть сигнал имеет вид, показанный на рис. 4.10 .

Разбиваем заданный сигнал на интервалы :

1.

;

2.

;

3.

.

Рис.4.10

При заданной импульсной функции цепи k(t) , выражения для расчета отклика выглядят следующим образом:

1-ый интервал

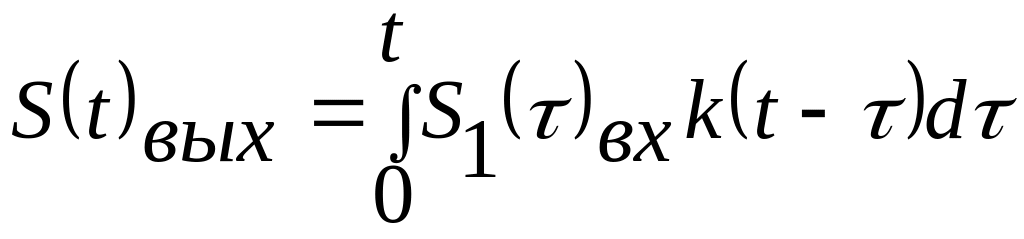, (4.15)

2-ой интервал

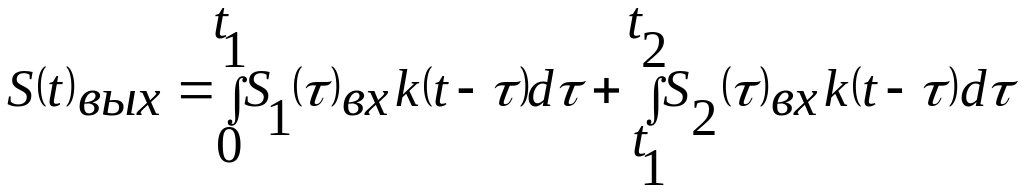, (4.16)

3-ий интервал

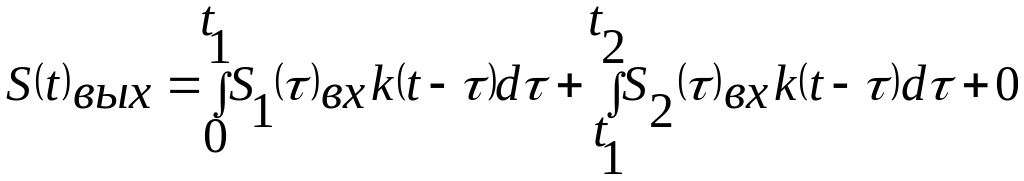. (4.17)

Из выражений 4.15-4.17 видно, что скачки в методе импульсных функций не учитываются.

ПРИМЕР 4.5

Сигнал S(t) вида (рис.4.11) подан на вход цепи с

;

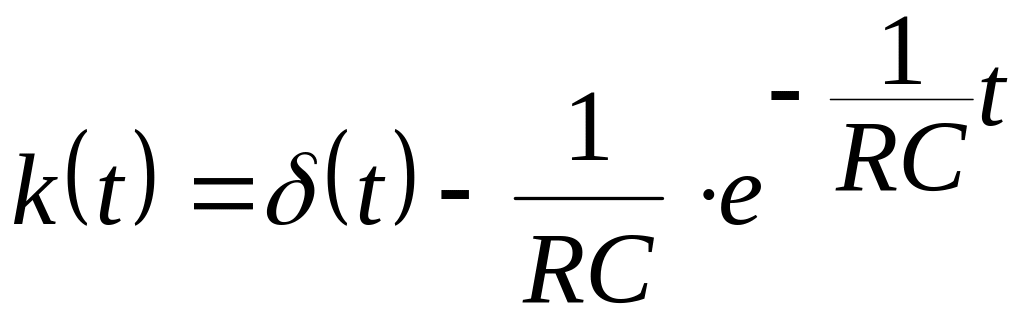Рис.4.11

Разбиваем заданный сигнал на интервалы:

1.Интервал

2.Интервал

Отклик заданной цепи определяется следующим образом:

1-ый интервал

.

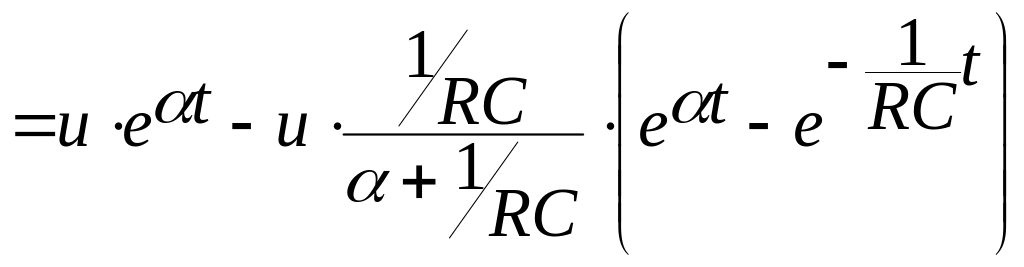2-ой интервал

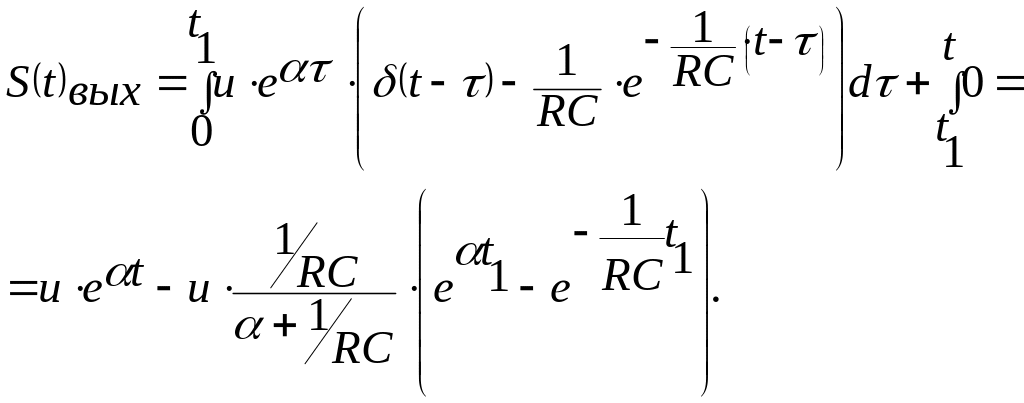
4.4 Связь между временными функциями линейных цепей

Для установления связи между и рассмотрим следую­щий пример.

П усть на вход цепи (рис. 4.12), заданной импульсной характеристикой подан сигнал вида , где S-постоянная величина.

Рис.4.12

Найдем выходной сигнал методом импульсных функций.

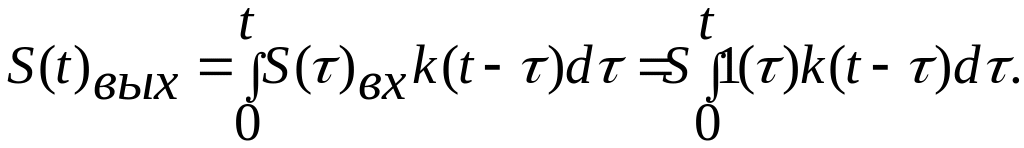
Положив для простоты и обозначая получим:

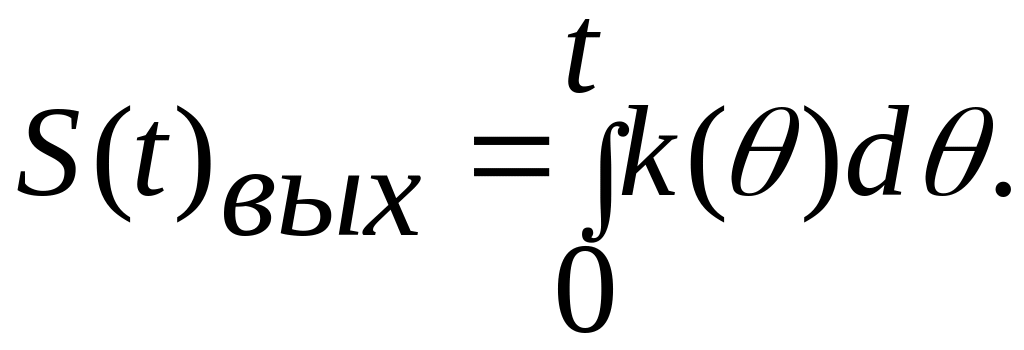
По определению отклик цепи на единичную функцию включения является переходной функцией цепи, поэтому:

(4.18)

дифференцируя правую и левую части (4.18) получим:

Соотношение (4.18) требует более внимательного рассмотрения.

1. Переходная функция h(t) не имеет скачка при t=0, h(0)=0. В этом случае справедливо соотношение (4.18).

ПРИМЕР 4.6

при t=0 ; h(0)=0

2. Переходная функция h(t) претерпевает скачок при t=0.

ПРИМЕР 4.7

при t=0 ; h(0)=A

В этом случае дифференцировать впрямую нельзя.

Выполняем следующие манипуляции:

(4.19)

в выражении (4.19) представляет собой функцию, повторяющую по форме h(t) без начального скачка (рис.4.13,а,б), и ее можно диф­ференцировать.

Учитывая также, что 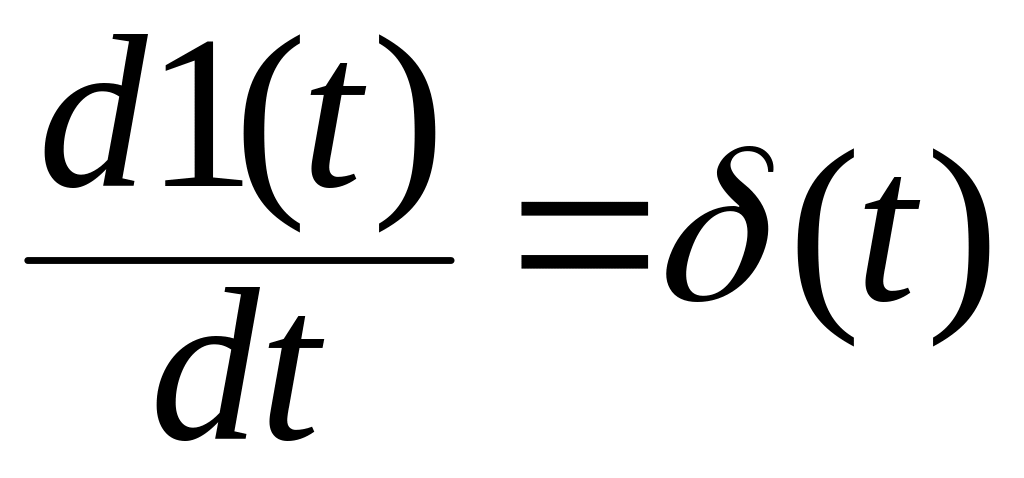,окончательно получим выражение для k(t):

(4.20)

Рис. 4.12

ПРИМЕР 4.8

5. ЭЛЕМЕНТЫ ТЕОРИИ СИГНАЛОВ И ЧАСТОТНЫЙ

АНАЛИЗ ЛИНЕЙНЫХ ЦЕПЕЙ

5.1. Разложение сигналов по системам взаимно-ортогональных

функций

Заданный сигнал S(t) при условии, что 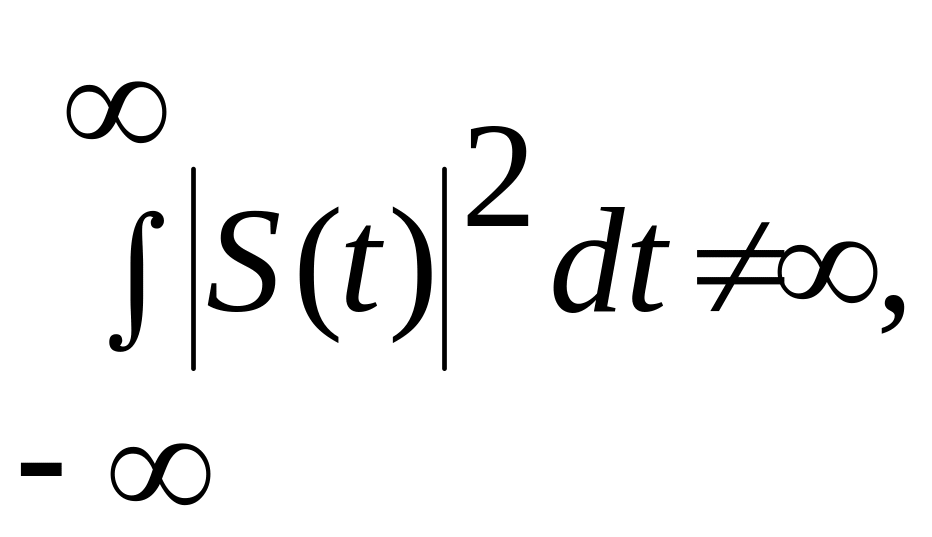т.е. энергия сигнала ограничена, что справедливо для всех реально существующих сигналов, можно разложить в ряд по системе взаимно-ортогональных функций .