3. Схемные функции электрических цепей

В технике связи чаще всего решается задача определения отклика электрической цепи при заданном воздействии. Для решения данной задачи вводится понятие об обобщенной цепи (рис. 3.1).

Рис. 3.1

При этом конфигурация и параметры обобщенной цепи не заданы, и цепь характеризуется схемной (системной) функцией, которая опреде­ляется соотношением между откликом y(t) и воздействием x(t):

схемная функция

Схемная функция цепи однозначно отражает свойства цепи, которые зависят от конфигурации (способа соединения элементов) и парамет­ров элементов, входящих в состав цепи.

Физически электрические сигналы отклик-воздействие представ­ляют собой изменяющиеся во времени токи или напряжения.

С точки зрения анализа сигналы могут быть заданы в виде времен­ных i (t), U(t); частотных I(j ), U(j ) или операторных I(P), U(P) функций и, соответственно, речь идет об анализе во временной или в частотной области или в операторной форме.

В табл.3.1 приведены схемные функции цепи и порождающие их комбинации отклик-воздействие.

Область определения схемных функций связана с областью задания сигналов и соответственно, как было показано выше, схемные функции определяются во временной ; … и т.д. или в частотной ; … или в операторной

; … .

Та б л и ц а 3.1

Воздействие	Отклик	Схемная Функция	Размерность
		Коэффициент передачи по току	-------
		Коэффициент передачи по напряжению	-------
		Переходное сопротивление	Ом
		Переходная проводимость	Сим
		Входное сопротивление	Ом
		Входная проводимость	Сим
		Выходное сопротивление	Ом
		Выходная проводимость	Сим

Примечание.

В дальнейшем схемные функции будем называть просто функциями цепи.

В общем виде, функции цепи выражаются следующими соотношениями:

; (3.1)

; (3.2)

Соотношения (3.1) и (3.2) определяют схемные функции цепи соответственно в частотной и операторной формах.

Примечание.

Временные функций цепи могут быть получены из (3.1) или (З.2), как будет показано ниже, путем применения соответственно обратного пре­образования Фурье или Лапласа .

Тестовые сигналы.

Для определения схемных функций электрических цепей при их экс­периментальном и теоретическом исследовании используется стандарт­ный набор сигналов воздействиятестовые сигналы.

Наиболее употребительными являются следующие:

единичный скачок;

единичный импульс;

единичная гармоническая функция.

Единичный скачок (единичная функция включения) обозначается символом 1(t), графически изображается, как показано на рис.3.2, и удовлетворяет следующим аналитическим соотношениям:

1(t)=0 t<0;

1(t)=1/2 t=0;

1(t)=1 t>0.

Рис. 3.2

Практически значение 1(t) в момент t=0 неуловимо, поэтому достаточно следующего набора соотношений:

В теории цепей используются модификации:

-запаздывающий единичный скачок (рис.3.3):

Рис. 3.3

- опережающий единичный скачок (рис.3.4).

Рис. 3.4

Умножение единичного скачка на постоянное число 1(t)E дает неединичный скачок с амплитудой E.

С помощью функции единичного скачка можно построить аналитичес­кое описание сложных сигналов.

ПРИМЕР З.1

Прямоугольный импульс (рис. 3.5,а) представлен в виде суммы двух неединичных скачков (рис. 3.5,б).

Рис. 3.5

ПРИМЕР 3.2

Запаздывающий синусоидальный сигнал (рис. 3.6).

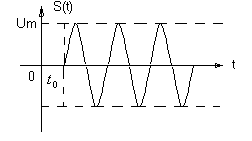
Рис. 3.6

Практически, единичный скачок реализуется, как прямоугольный им­пульс, длительность которого значительно превышает постоянную вре­мени цепи, на которую действует данный импульс.

Единичный импульс обозначается символом .

Единичный импульс представляет собой идеализированный прямо­угольный импульс с бесконечно большой амплитудой и с бесконечно малой длительностью. При этом площадь S единичного импульса долж­на быть равна единице.

Примечание. Импульс с будем называть неединичным импульсом.

Рассмотрим прямоугольный импульс (рис. 3.7):

,

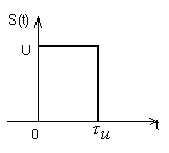
где Bкоэффициент, выравнивающий размерность и численно равный единице.

Рис. 3.7

Площадь импульса:

Идеальный единичный импульс получается при ,

при этом .

Представим единичный импульс с помощью суммы единичных скачков (рис 3.8).

Рис. 3.8

;

; производная от функции 1(t).

обозначается ,

дельта-функция или функция Дирака  является математи­ческим отображением единичного импульса (рис. 3.9 - 3.11).

Основные свойства функции.

Рис. 3.9

Запаздывающая дельта-функция:

Рис. З.10

О пережающая дельта-функция:

Рис. 3.11

Фильтрующее свойство дельта функции:

; (3.3)

. (3.4)

Соотношения (3.3), (3.4) представляют собой интегралы свертки функ­ции c функцией. Результатом выполнения операции сверт­ки является значение функции "выборка" в точке существо­вания функции (рис. 3.12) .

Рис.3.12 Рис.3.13

Практически единичный импульс реализуется в виде короткого им­пульса, длительность которого значительно меньше постоянной вре­мени цепи, на которую действует данный импульс.

Единичная гармоническая функция обозначается символом 1(j ) и представляет собой синусоидальное колебание с амплитудой, равной единице, и с нулевой начальной фазой; текущая частота.

Временные функции электрических цепей.

Переходная функция электрической цепи обозначается символом h(t) и является откликом данной цепи на воздействие единичного скачка (рис. 3.13).

Рис. 3.13

Импульсная функция электрической цепи обозначается символом k(t)и является откликом данной цепи на воздействие единичного импульса (рис. З.14).

Рис. 3.14

Переходные и импульсные характеристики заданных цепей аналити­чески определяются методами анализа переходных процессов в линей­ных цепях. В основном используется операторный метод.

Экспериментально переходные характеристики исследуются с по­мощью прибора ”Измеритель переходных характеристик” (ИПХ). Принцип действия прибора поясняется на рис.3.15.

Рис. 3.15

Рассмотрим примеры вычисления переходных и импульсных характеристик.

ПРИМЕР 3.3