
- •18. Определение производной функции в точке.
- •19. Определение дифференцируемой функции в точке x0 .
- •20. Определение дифференциала функции f(X ) в точке x0 .
- •41. Достаточное условие интегрируемости.
- •42. Геометрический смысл определенного интеграла.
- •43. Свойства определенного интеграла.
- •49. Определение несобственного интеграла от неограниченной функции на ограниченном промежутке.
- •51.Окрестность точки в Rn . Внутренние и граничные точки множества.
- •52. Открытые и замкнутые множества.
- •53.Изолированные и предельные точки множества.
- •54.Ограниченные множества.
- •81.Сведение кратного интеграла к повторному интегралу.
- •82. Формула замены переменных в двойном интеграле. Использование полярных координат для вычисления двойных интегралов.
- •83. Геометрические приложения двойных интегралов: вычисление площадей плоских фигур и объемов пространственных тел.
- •84. Несобственные кратные интегралы. Интеграл Эйлера-Пуассона.
- •85. Числовые ряды.
- •86. Последовательность частичных сумм. Сумма ряда. Сходящиеся ряды.
- •87. Свойства сходящихся рядов.
- •88. Необходимое условие сходимости числового ряда.
- •89. Числовые ряды с неотрицательными членами.
- •90. Критерий сходимости числовых рядов с неотрицательными членами.
- •91. Признаки сравнения, признак Даламбера и Коши, интегральный признак для числовых рядов с неотрицательными членами.
- •92. Знакопеременные ряды. Абсолютная и условная сходимость.
- •97. Интегрируемость и дифференцируемость суммы степенного ряда на интервале сходимости.
- •107. Общее решение однородного дифференциального уравнения с
- •109. Общее решение однородной системы линейных
1. Определение числовой функции. Способы задания функций.
Пусть D – множество на числовой прямой R. Если каждому х принадлежащему D поставлено в соответствие единственное число y=f(x), то говорят, что задана функция f.
Способы задания функций:
1) табличный – для функций, заданных на конечном множестве.
2) аналитический
3) графический
2 и 3 – для функций, определенных на бесконечном множестве.
2. Понятие обратной функции.
Если функция y=f(x) такова, что разным значениям х аргумента соответствуют разные значения у функции, то переменную х можно выразить как функцию переменной у: x=g(y). Функцию g называют обратной к f и обозначают f^(-1).
3. Понятие сложной функции.
Сложная функция- функция, аргументом которой является другая любая функция.
Пусть даны функции f(x) и g(x). Составим из них две сложные функции. Считая функцию f внешней (главной), а функцию g – внутренней, получаем сложную функцию u(x)=f(g(x)).
4. Определение предела последовательности.
Число
а называется пределом последовательности
{xn}, если для любого
положительного ![]() существует номер n0, начиная
с которого все члены посл-ти отличаются
от а по модулю меньше, чем на ε (т.е.
попадают в ε-окрестность точки а):
существует номер n0, начиная
с которого все члены посл-ти отличаются
от а по модулю меньше, чем на ε (т.е.
попадают в ε-окрестность точки а):
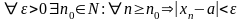
5. Правила вычисления пределов сходящихся последовательностей.
1.Всякая
сходящаяся последовательность имеет
только один предел. 2. Если все элементы
последовательности {xn}
равны С (постоянной), то предел
последовательности {xn},
тоже равен С. 3.
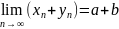 ;
4.
;
4.
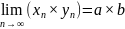 ;
5.
;
5.
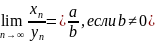 .
.
6. Определение ограниченной последовательности.
Посл-ть
{xn}
называется ограниченной, если множество
чисел X={xn}
ограниченно:
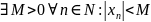 .
.
7. Определение бесконечно малой последовательности.
Посл-ть
{xn}
наз-ют бесконечно малой, если для любого
(сколь угодно малого)
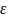 >0
найдется такой номер n0,
что для всякого n>n0
выполняется нерав-во |xn|<
.
>0
найдется такой номер n0,
что для всякого n>n0
выполняется нерав-во |xn|<
.
8. Определение бесконечно большой последовательности.
Посл-ть наз-ют бесконечно большой, если для любого (сколь угодно большого) числа А>0 найдется такой номер n0, что для всякого номера n>n0 выполняется нерав-во |xn|>A.
9. Определение монотонных последовательностей.
Монотонные
посл-ти: 1) возрастающая, еслиxn<xn+1
для всех n, 2) неубывающая,
еслиxn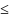 xn+1
для всех n, 3) убывающей,
еслиxn>xn+1
для всех n, 4) невозрастающей,
еслиxn
xn+1
для всех n, 3) убывающей,
еслиxn>xn+1
для всех n, 4) невозрастающей,
еслиxn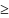 xn+1
для всех n.
xn+1
для всех n.
10. Определение предела функции в точке.
Пределом
ф-ии y=f(x)
в точке x0 (или при
x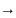 x0)
наз-ют число а, если для любой посл-ти{xn}
значений аргумента, сходящейся к х0
(при этом все xn
x0)
наз-ют число а, если для любой посл-ти{xn}
значений аргумента, сходящейся к х0
(при этом все xn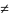 x0),
посл-ть {f(xn)}
значений ф-ии сходится к пределу а.
x0),
посл-ть {f(xn)}
значений ф-ии сходится к пределу а.
11. Определение бесконечно малой функции.
Ф-ия
f(x) наз-ся
бесконечно малой при х→А, если
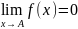 .
.
12. Определение бесконечно большой функции.
Ф-ия
f(x) наз-ся
бесконечно большой при х→А, если
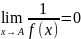 .
.
13. Первый замечательный предел.
Первым
замечательным пределом называется
предел
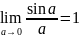
14. Второй замечательный предел.
Вторым
замечательным пределом называется
предел
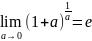 .
.
15. Определения односторонних пределов функции в точке.
Число
а наз-ют пределом ф-ии f(x)
в точке x0 справа,
если для любой сходящейся к х0
посл-ти{xn},
у которой все х0>xn,
соотв-щая посл-ть {f(xn)}
сходится к а:
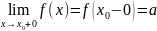
Предел
ф-ии f(x) в
точке x0 слева:
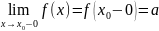 .
.
16. Определение функции, непрерывной в точке.
Пусть
ф-ия f(x)
определена в окрестности точки х0.
Ф-ию f(x)
наз-ют непрерывной в точке x0,
если
 сущ-ет и равен f(x0):
сущ-ет и равен f(x0):
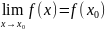 .
.
17. Определение точки разрыва функции. Классификация точек
разрыва.
Точку
х0 наз-ют точкой разрыва ф-ии f(x),
если f(x) не
является непрерывной в х0, т е в
люб из трех случаев: 1) ф-ия не опред-на
в х0 2)
не сущ-ет 3)
 .
.
Типы
точек разрыва 1. x0
– точка устранимого разрыва, если
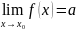 (|a|<
(|a|<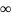 ),
но значение f(x0)
либо не опред-но, либо не равно а. 2. x0
– точка разрыва I порядка,
если сущ конечные односторонние пределы
в точке, но они не равны. В этом случ
разность
),
но значение f(x0)
либо не опред-но, либо не равно а. 2. x0
– точка разрыва I порядка,
если сущ конечные односторонние пределы
в точке, но они не равны. В этом случ
разность
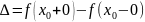 наз-ют
скачком ф-ии в х0. 3. x0
– точка разрыва II порядка,
если хотя бы один из односторонних
пределов ф-ии в точке не сущ-ет или равен
.
наз-ют
скачком ф-ии в х0. 3. x0
– точка разрыва II порядка,
если хотя бы один из односторонних
пределов ф-ии в точке не сущ-ет или равен
.
18. Определение производной функции в точке.
Производной
ф-ии y=f(x)
в точке х=х0 наз-ют предел
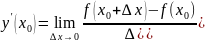 .
.
19. Определение дифференцируемой функции в точке x0 .
Ф-ию
f(x) наз-ют
дифференцируемой в точке x0,
если предел
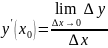 существует и конечен.
существует и конечен.
20. Определение дифференциала функции f(X ) в точке x0 .
Дифференциалом
ф-ии наз-ют выражение
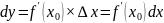 .
.
21. Теорема о производной сложной функции.
Если
функция
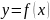 дифференцируема в точке
дифференцируема в точке
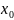 ,
а функция
,
а функция
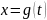 дифференцируема в точке
дифференцируема в точке
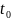 и
и
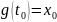 ,
то сложная функция
,
то сложная функция
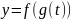 также дифференцируема в
и выполняется следующее равенство
также дифференцируема в
и выполняется следующее равенство

22. Теорема о производной обратной функции.
Если
функция
имеет обратную функцию
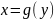 и в точке
и в точке
 производная
производная
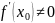 ,
то обратная функция
,
то обратная функция
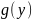 дифференцируема в точке
дифференцируема в точке
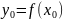 и
и

23. Геометрический смысл производной и дифференциала.
Геометрический
смысл производной
состоит в том, что
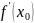 – это тангенс угла наклона касательной
к графику
в точке
– это тангенс угла наклона касательной
к графику
в точке
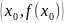
Дифференциал
функции
 соответствующей данным значениям x и
Δx, равен приращению ординаты касательной
к функции
в данной точке х.
соответствующей данным значениям x и
Δx, равен приращению ординаты касательной
к функции
в данной точке х.
24. Уравнение касательной.
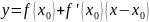
25. Определение эластичности функции.
Если
– дифференцируемая функция, то ее
эластичностью в точке
называется предел
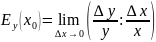
26. Теорема Лопиталя. Правило Лопиталя.
Предположим,
что функции
и
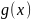 дифференцируемы в окрестностях точки
и будем считать, что аргумент
стремится к
дифференцируемы в окрестностях точки
и будем считать, что аргумент
стремится к
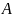 ,
где под
понимается число или символ бесконечности.
Тогда, если
,
где под
понимается число или символ бесконечности.
Тогда, если
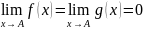 или
или
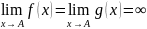 ,
то
,
то
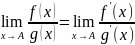
27. Производные и дифференциалы высших порядков.
Результат
-кратного
дифференцирования функции
обозначают
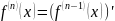 и называют производной порядка
и называют производной порядка
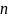 .
.
28. Формула Тейлора. Формула Маклорена.
Формула Тейлора

Формула Маклорена
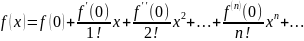
29. Признак монотонности дифференцируемой функции.
Если
 ,
то функция убывает, если
,
то функция убывает, если
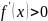 ,
то функция возрастает.
,
то функция возрастает.
30. Определение локального экстремума функции одной переменной.
Точку
называют точкой
локального максимума (минимума)
функции
,
если существует некоторая окрестность
этой точки, в которой для всех
выполняется неравенство
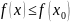
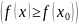 .
Точки локального максимума и минимума
называют точками
локального экстремума.
.
Точки локального максимума и минимума
называют точками
локального экстремума.
31. Необходимое условие локального экстремума функции одной
переменной.
Пусть
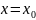 – точка локального экстремума функции
,
дифференцируемой в некоторой окрестности
точки
.
Тогда
– точка локального экстремума функции
,
дифференцируемой в некоторой окрестности
точки
.
Тогда

32. Точка перегиба функции.
Точку
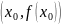 называют точкой перегиба функции
,
если в этой точке выгнутость меняется
на вогнутость или наоборот.
называют точкой перегиба функции
,
если в этой точке выгнутость меняется
на вогнутость или наоборот.
33. Необходимое условие точки перегиба.
Пусть
– точка перегиба функции
,
дважды дифференцируема в некоторой
окрестности точки
.
Тогда

34. Определение асимптот графика функции.
Асимптотой функции называют прямую, к которой приближаются точки графика функции при бесконечном удалении их от начала координат.
35.Определение первообразной для функции f (x) на промежутке X .
Функция
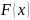 называется первообразной для функции
на промежутке X,
если для любого значения
из этого промежутка выполняется равенство
называется первообразной для функции
на промежутке X,
если для любого значения
из этого промежутка выполняется равенство
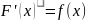
36. Определение неопределенного интеграла.
Множество
всех первообразных функции
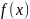 называют неопределенным интегралом от
этой функции и обозначают
называют неопределенным интегралом от
этой функции и обозначают

37. Свойства неопределенного интеграла.
Производная неопределенного интеграла равна подынтегральной функции, т.е.
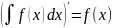
Неопределенный интеграл равна от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
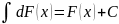
Постоянный множитель можно выносить за знак неопределенного интеграла, т.е. для любого числа k
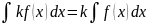
Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых, т.е.
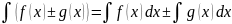
38.Формула замены переменной в неопределенном интеграле.
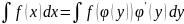
где
 – обратимая дифференцируемая на
рассматриваемом промежутке функция
– обратимая дифференцируемая на
рассматриваемом промежутке функция
39. Формула интегрирования по частям для неопределенного интеграла.
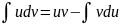
40. Определение определенного интеграла Римана.
Пусть
на отрезке
 определена
вещественнозначная функция
определена
вещественнозначная функция
![]() .
.
Рассмотрим
разбиение
отрезка
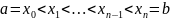 - конечное множество попарно различных
точек отрезка. Это разбиение делит
отрезок
на n
отрезков
- конечное множество попарно различных
точек отрезка. Это разбиение делит
отрезок
на n
отрезков
 ,
i=1…n.
Длина наибольшего из отрезков
,
i=1…n.
Длина наибольшего из отрезков
 , называется шагом
разбиения,
где
, называется шагом
разбиения,
где
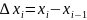 — длина отрезка.
— длина отрезка.
Отметим
на каждом отрезке разбиения по точке
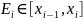 .
Интегральной
суммой
называется выражение
.
Интегральной
суммой
называется выражение
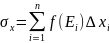 .
.
Если
при стремлении шага разбиения к нулю
интегральные суммы стремятся к одному
и тому же числу, независимо от выбора
,
то это число называется интегралом
функции
на
отрезке
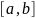 ,
т.е.
,
т.е.
 .
.
В этом случае, сама функция называется интегрируемой (по Риману) на ; в противном случае является неинтегрируемой (по Риману) на отрезке .
