§11. Передаточные функции звеньев

Передаточные функции (п.ф.) могут быть определены двумя способами:

- в операторной форме;

- в изображениях по Лапласу.

Рассмотрим нахождение п.ф. в операторной форме применительно к уравнению звена второго порядка (см. выше). П.ф. в операторной форме равна отношению оператора входного воздействия к собственному оператору звена. Количество передаточных функций равно количеству входных величин звена при одной выходной:

-п.ф. по x₁ относительно y,

-п.ф. по x₂ относительно y.

Уравнение в операторной форме с применением п.ф. имеет вид:

y=W₁(p)x₁+W₂(p)x₂.

П.ф. в изображениях по Лапласу равна отношению изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях (ННУ) и равенстве нулю всех остальных входных величин. Изображение по Лапласу функции у(t) находится в виде определенного интеграла:

, где s=α+jω, .

s - комплексная переменная преобразования Лапласа .

Изображение по Лапласу первой производной находится по аналогичной формуле с использованием интегрирования по частям :

.

Аналогично изображение второй производной

.

Значения у(0), (0),....., y^(n-1)(0) представляет собой начальные условия, n - порядок уравнения.

Если подвергнуть преобразованию Лапласа левую и правую часть дифференциального уравнения, то в результате будет получено уравнение для изображений. Это уравнение будет алгебраическим, что упрощает расчет операторным методом. Наиболее просто это уравнение будет выглядеть при нулевых начальных условиях, а именно, оно будет совпадать с уравнением в операторной форме при замене p на s:

(T₀²s²+T₁s+1)Y(s)=k₁(T₂s+1)X₁(s)+k₂X₂(s).

Найдем отсюда передаточные функции. Они получаются формально совпадающими с п.ф. в операторной форме при замене p на s:

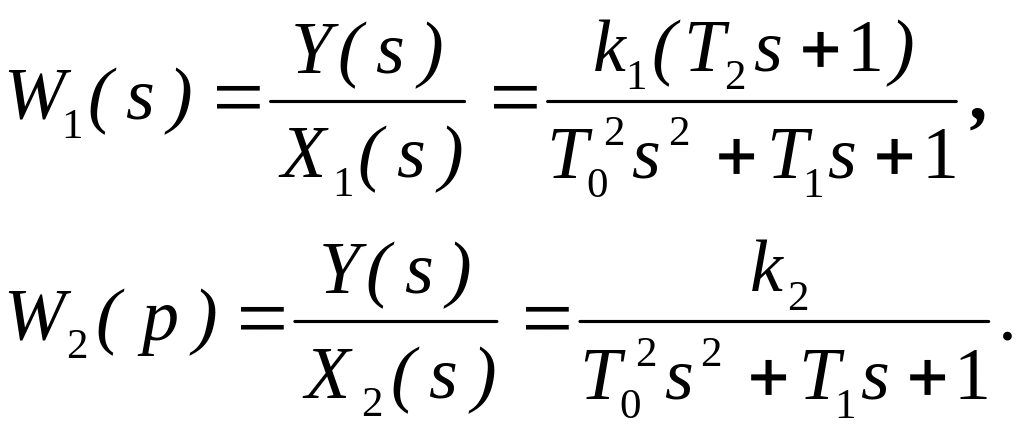
Уравнение в изображениях: Y(s)=W₁(s)X₁(s)+W₂(s)X₂(s).

Знаменатель y п.ф. одинаков в W₁(s) и W₂(s) и называется характеристическим полиномом:

A(s)=T₀²s²+T₁s+1.

Приравнивая к нулю характеристический полином, получаем следующее характеристическое уравнение T₀²s²+T₁s+1=0, корни которого характеризуют динамические свойства звена, а именно устойчивость и качество переходного процесса (число корней равно порядку уравнения).

Если звено (система) нестационарно, то п.ф. в изображениях по Лапласу находится в результате более сложного расчета и не совпадает по виду с п.ф. в операторной форме.

Запишем в общем виде уравнение нестационарного звена:

Уравнение можно записать в операторной форме:

A(p,t)y=B(p,t)x, где A(p,t)=a₀(t)pⁿ+…+a_n-1(t)p+a_n(t),

B(p,t)=b₀(t)p^m+…+b_m(t). Передаточная функция в операторной форме:

Уравнение звена в сокращенном виде: y=W(p,t)x.

П.ф. в изображениях по Лапласу находится в виде бесконечного ряда:

W(s,t)=W₀(s,t)+W₁(s,t)+…

Чем больше членов здесь взято, тем с большей точностью она определяется. Здесь - п.ф. нулевого приближения;

W_r(s,t)- называется поправкой и находится по рекуррентной формуле

r=1,2,…,

где - оператор с комплексными зависящими от времени коэффициентами.

Если коэффициенты меняются сравнительно медленно, то соответствующий процесс называется квазистационарным, и для него могут быть применены так называемые передаточные функции с «замороженными» коэффициентами. Они обозначаются W₀(s,t_i) и находится из п.ф. нулевого приближения: ,

где t_i некоторый момент рассматриваемого процесса. Для уточнения расчета переходный процесс может быть разбит на отрезки, для каждого из которых находится своя передаточная функция с «замороженными» коэффициентами.