24. . Задача программирования оптимального управления

Рассмотрим линейную динамическую систему

, , , , (3.51)

где и - матрицы порядков и , зависящие от времени, - фиксировано, - управление.

Критерий оптимальности зададим в виде

, (3.52)

где и - положительно определенные матрицы порядков и , зависящие от времени.

Для определения оптимального управления , минимизирующего функционал , используем принцип максимума. Составим гамильтониан

. (3.53)

Оптимальное управление для простоты полагаем неограниченным и определяем из условий максимума :

.

Так как 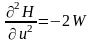, то условие положительной определенности матрицы обеспечивает максимум . Следовательно, в соответствии с первым условием оптимальный закон управления имеет вид программного управления

. (3.54)

Каноническая система уравнений принимает вид

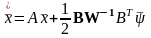, , (3.55)

, .

Задача оптимального управления сведена к краевой задаче для системы линейных дифференциальных уравнений. Эту задачу можно решать, например, используя фундаментальную матрицу системы линейных однородных уравнений [1].

2. Задача синтеза оптимального управления

Рассмотрим задачу синтеза оптимального управления системой

, , ,

из условия обращения в минимум критерия оптимальности

. (3.56)

Полагаем, что , , , - матрицы, зависящие от времени, причем , , - положительно - определенные, - постоянная матрица коэффициентов, - фиксировано.

Как и в предыдущей задаче, в соответствии с принципом максимума оптимальное управление определяется зависимостью (3.54)

. (3.57)

Каноническая система уравнений имеет также прежнюю структуру, но другие граничные условия:

, , (3.57)

, (3.58)

.

Будем искать решение второго уравнения в ви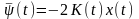де , где - неизвестная матрица переменных коэффициентов. Для нее можно получить уравнение, которое позволит найти ее непосредственно. Подставив в (3.58), после преобразований получим

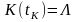, . (3.59)

Это уравнение представляет собой нелинейное матричное дифференциальное уравнение Риккати. Решая уравнение (3.59) «справа налево» определяем 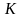, и закон оптимального управления:

. (3.60)

Данный закон называется оптимальным линейным регулятором.

Замечание. Если , , , не зависят от времени, то при достаточно большом можно говорить об «установившемся» режиме. В этом случае можно положить . Тогда матрица является постоянной и определяется из линейного матричного алгебраического уравнения:

. (3.61)

Решение этого уравнения можно рассматривать как предел (если он существует) решения дифференциального уравнения Риккати при .

25. Рассмотрим следующую задачу синтеза оптимального управления линейной динамической системой

, , , (4.16)

,

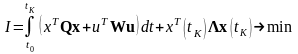где матрицы , , , и в общем случае зависят от времени, причем и - положительно – определенные, матрица - постоянная.

Запишем уравнение Беллмана для системы (4.16)

(4.17)

с граничным условием

. (4.18)

Сначала будем решать задачу, сняв ограничения на управление. Тогда, осуществляя операцию минимизации в (4.17), получим

, . (4.19)

Тогда уравнение (4.17) принимает вид

. (4.20)

Решение этого уравнения будем искать в виде

, (4.21)

где - симметрическая матрица порядка ( ). Сравнивая (4.21) с (4.18), видим, что

. (4.22)

Подставляя (4.21) в (4.20), получим

(4.23)

Отсюда следует, что матрица должна удовлетворять уравнению

, (4.24)

которое может быть решено путем интегрирования от до с граничным условием (4.22). Это уравнение есть уже известное по предыдущей главе уравнение Риккати. Заметим, что проблемой при его решении может быть наличие «особых точек», то есть точек разрыва второго рода.

С учетом выражения (4.21) для функции будущих потерь получаем оптимальное управление в форме оптимального линейного регулятора

, (4.25)

где . (4.26)

Вернемся к первоначальной постановке задачи, учитывая ограничение на управление. Если , то проблемы не существует. В общем случае оптимальное управление состоит из двух режимов: (4.25) и граничного ( - граница множества ). Сложность заключается в том, что теперь для функции не существует единого выражения для всего пространства . При граничном управлении функция 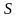отличается от квадратичной формы и может быть найдена путем решения уравнения Беллмана с граничным управлением, например, методом характеристик, с последующей гладкой склейкой полученного решения и решения (4.21).

Рассмотренная выше задача называется задачей аналитического конструирования оптимальных регуляторов (задача АКОР).

26. В общем случае под вырожденной задачей понимают такую, в которой максимизация гамильтониана по управлению не позволяет получить в явном виде выражения для оптимального управления. Тем не менее оптимальное управление, называемое особым, может существовать.

Рассмотрим случай, когда гамильтониан линейно зависит от управления. Пусть динамическая система описывается дифференциальным уравнением

, , ,

где - вектор размерности , , - вектор-функции размерности , - скалярная переменная, - свободно.

Критерий оптимальности зададим в виде .

Составим гамильтониан

, (3.62)

где , 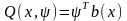. (3.63)

Если на некотором отрезке 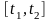, то гамильтониан не зависит от , оптимальное управление не может быть найдено из условия максимизации . Получим дополнительные необходимые условия, которым оно должно удовлетворять. Согласно необходимым условиям оптимальности для задачи Майера, если свободно, то , и, следовательно, . Тогда

, (3.64)

(3.65)

для всех значений и любого .

Раскроем эти выражения для различных . Пусть :

. (3.66)

. (3.67)

Следовательно, условия равенства нулю первых производных выполняются при любом , если имеет место равенство

, (3.68)

где . (3.69)

Получим выражения для случая

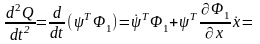
, (3.70)

где , (3.71)

. (3.72)

Если 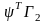не обращается в нуль, то особое управление имеет вид:

. (3.73)

Это управление является искомым особым управлением, если выполняется ограничение .

Однако, если , то особое управление по-прежнему не находится в явном виде из (3.73). Выражение (3.70) примет вид:

. (3.74)

Можно показать, что последовательное дифференцирование однотипных выражений (3.68), (3.74)… в конечном итоге приведет нас при , то есть при четных значениях производных к уравнению, в котором коэффициент при не равен нулю.

, (3.75)

откуда получаем управление

: (3.76)

которое может являться искомым особым управлением, если выполняется ограничение

. (3.77)

Технология отыскания особых управлений не изменяется для вектора управлений любой размерности, а также для случая, когда фиксировано: коэффициенты при каждой компоненте вектора подвергаются дифференцированию до тех пор, пока особое управление не будет определено в явном виде.

Сформулируем теперь необходимые условия оптимальности особого управления. Исследование этой проблемы ведется с использованием математического аппарата двусторонних вариаций управления, которые называются вариациями Келли (рис. 3.4).

Рис. 3.4. Вариация Келли

Вариация управления, предложенная Келли, представляет собой двусторонний равный по интенсивности скачок управления, причем на отрезке и вариации имеют противоположные знаки. Доказано, что реакция динамической системы на вариацию Келли есть величина более высокого порядка малости, чем реакция на обычную игольчатую вариацию, таким образом (рис. 3.5), где - вектор-функция правых частей в математической модели непрерывной динамической системы.

Рис. 3.5. Реакция динамической системы на:

1) одностороннюю игольчатую вариацию,

2) на вариацию Келли

Запишем необходимые условия минимума функционала при особом управлении

, .

Используя аппарат вариаций Келли, можно получить выражение для второй вариации в следующем виде [2] :

, (3.78)

где представляет собой выражение

. (3.79)

Видно, что представляет собой коэффициент при управлении в выражении (3.70), полученном при двукратном дифференцировании функции 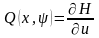. Таким образом, условие

(3.80)

является необходимым условием оптимальности управления. Это условие называется условием Келли-Брайсона.

Структура оптимального решения в вырожденных задачах оптимального управления состоит из чередующихся участков регулярного управления (которое определяется из условия: ) и особого управления , а в точках сопряжения регулярного и особого участков может иметь место разрыв 1-го рода функции .